DDPM背后的数学原理

Understanding Diffusion Models: A Unified Perspective -论文笔记

🔗生成式模型介绍

已知一个感兴趣分布的观测样本x,生成式模型目标是去学习建模它的真实数据分布p(x).

作用：

任意生成一个新样本
评估观测或采样数据的似然

现有的生成模型综述：

GAN:以对抗的方式建模一个复杂分布的采样过程
基于似然的生成模型：学习一个能够使观测样本具有高似然的模型。比如自回归模型、归一化流、VAE。
基于能量函数建模：通过学习一个任意灵活的能量函数来表示分布，然后对其进行归一化。
基于分数的生成模型：不对能量函数本身建模，而是学习基于能量模型的分数，并将其表达为一个神经网络。

🔗背景：ELBO,VAE,HVAE

Latent Variable: 对于许多模态，可以考虑我们的观测样本是由一个相关的看不见的潜在变量来表征或生成的。这个潜在变量即隐变量用z表示，比如一张图片可以由颜色、大小、形状等抽象特性表征。

🪄Evidence Lower Bound

为什么选用ELBO下界？

上述推导可得最大似然 = ELBO+KL散度，最大化ELBO，KL散度越近于0，那么近似分布越接近于真实分布。

🪄Variational Autoencoders

重参数化技巧(reparameterization trick)

上面推导中 $z^l$ 是随机采样的随机变量，无法计算梯度。通过将随机性转移到固定噪声 ϵ 上，z 的计算过程变成可导的（μ 和 σ直接参与计算），梯度可以通过 μ和 σ反向传播。

$x = \mu+\sigma*\epsilon\quad\epsilon\sim N(0,I)$

🪄Hierarchical Variational Autoencoders

HVAE变分自编码器（VAE）的一种推广形式，它扩展到了潜在变量的多层次结构。在这种框架下，潜在变量本身被解释为由其他更高层次、更抽象的潜在变量生成。

MHVAE:生成过程是一个马尔科夫链；每个潜在变量 $z_t$ 的仅依赖于前一个潜在变量 $z_{t+1}$ .

🔗Variational Diffusion Models

扩散模型 本质就是一个 MHVAE，但是有三个限制。

潜变量z的维度与原数据x保持一致
潜在编码器的高斯参数随时间变化，使得潜在的时间步长T(即最终潜在分布)的分布是标准高斯分布
每个时间步的潜在编码器的结构不是学习的; 它被预先定义为线性高斯模型。换句话说，它是一个以上一个时间步长的输出为中心的高斯分布。(马尔科夫性质)

以上限制描述的是输入图像随着时间逐渐被噪声化为一个 纯噪声图-标准高斯分布。其中 $q(x_t|x_{t-1})$ 过程被建模为高斯分布，每个时间步有定义的均值和方差参数，是固定的不需要学习。

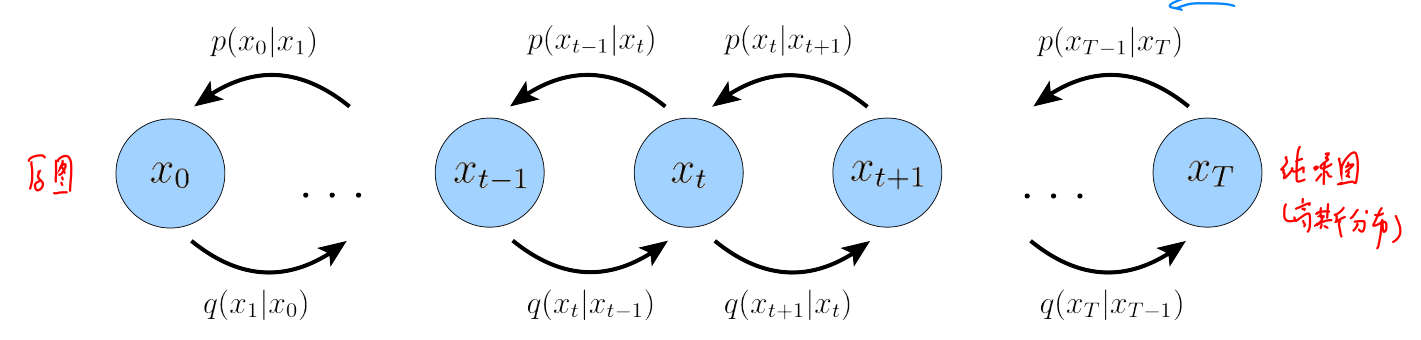
同HVAE、VDM也可以通过最大化ELBO进行优化：

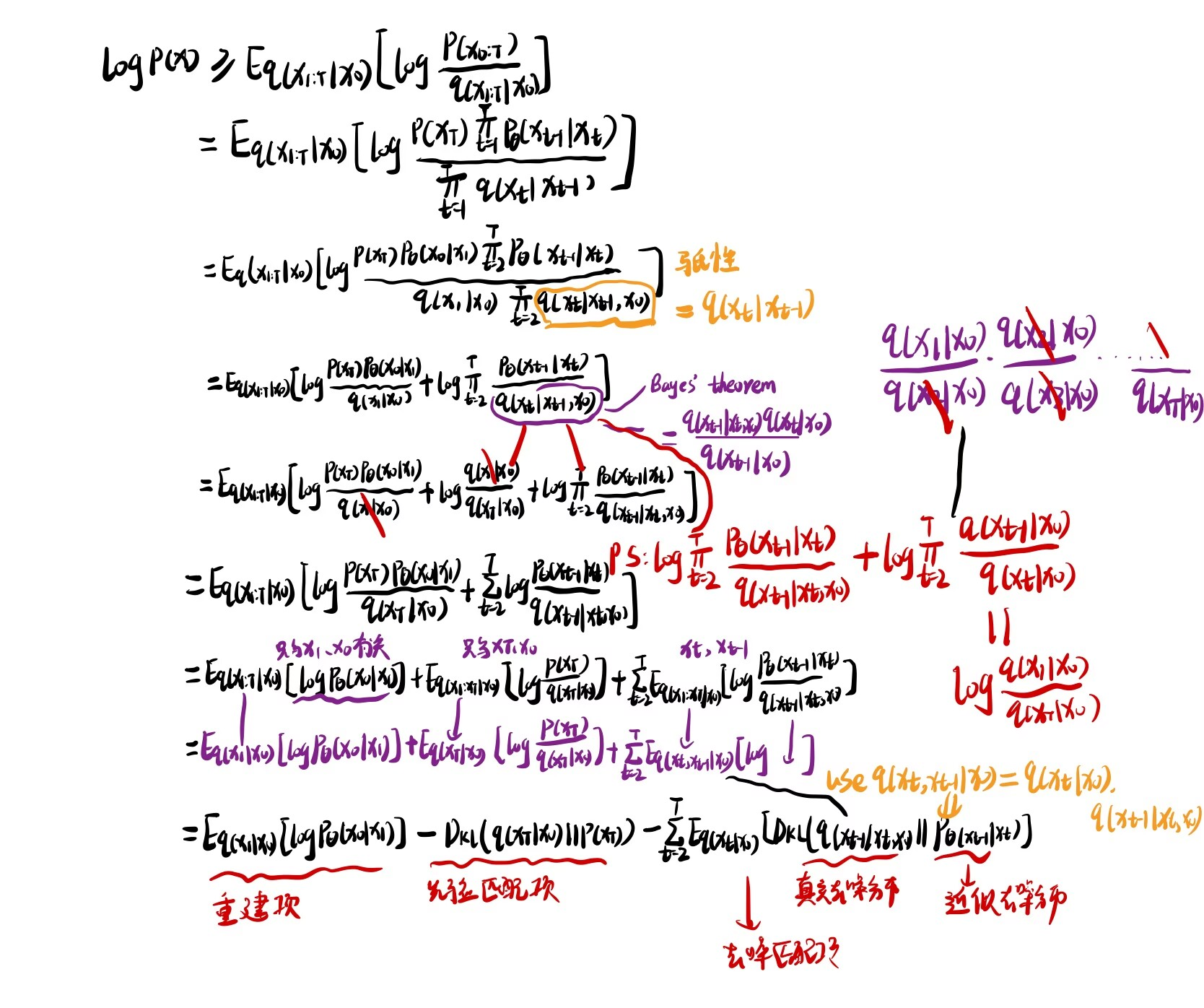
重建项：类似VAE中的重建项，可以同过蒙特卡洛近似求解
先验匹配项：度量最终生成的高斯分布跟先验的标准高斯分布的接近程度；在给定 $\alpha$ 情况下该项确定的，不需要优化
去噪匹配项：该项通过学习参数使近似去噪分布 $P_\theta(x_{t-1}|x_t)$ 尽可能逼近 真实去噪分布 $q(x_{t-1}|x_t,x_0)$ ,最小化 KL 散度

因此可以发现我们唯一需要优化的项只有第三项denoising matching term.

🪄真实去噪分布如何求得？

根据贝叶斯定理：

$q(x_{t-1}|x_t,x_0)=\frac{q(x_{t}|x_{t-1},x_0)q(x_{t-1}|x_0)}{q(x_t|x_0)}$

因此我们分别求出 $q(x_{t}|x_{t-1},x_0)q(x_{t-1}|x_0)q(x_t|x_0)$ 三项即可。

根据马尔可夫性质，我们可以知道 $q(x_t|x_{t-1},x_0)=q(x_t|x_{t-1})=N(x_t;\sqrt[]{\alpha_t}x_{t-1},\sqrt[]{1-\alpha_{t-1}}I)$ ,这一步来自于(上文提过)假设2 每一步Encoder固定为高斯模型。

1.1 因此根据假设我们首先求得 $q(x_t|x_{t-1},x_0)$ 项：

$x_t = \sqrt[]{\alpha_t}x_{t-1}+\sqrt[]{1-\alpha_t}\epsilon\quad with\quad\epsilon\sim N(0,I)$

1.2 根据递归原理 求取 $q(x_{t-1}|x_0)q(x_t|x_0)$ 两项(重参数化技巧上文有提到哦)

1.3 将上面每一式的分布求出后，很自然可以得到 $q(x_{t-1}|x_{t},x_0)$ 项

这里就是把三项的高斯分布带进去计算，下图摘自论文的过程。

🪄KL散度如何计算？

现在已经求得真实去噪分布 $q(x_{t-1}|x_{t},x_0)$ 项的形式，那么如何计算denoising matching term中的KL散度值呢？

首先已知两个高斯分布之间的KL散度公式如下(来自PRML这本书)：

$D_{KL}(N(x;\mu_x,\mathbf{\Sigma}_x)||N(y;\mu_y,\mathbf{\Sigma})_y)=\frac{1}{2}[log\frac{\mathbf{\Sigma}_y}{\mathbf{\Sigma}_x}-d+tr(\mathbf{\Sigma}^{-1}_y\mathbf{\Sigma}_x)+(\mu_y-\mu_x)^T\mathbf{\Sigma}^{-1}_y(\mu_y-\mu_x)]$