​ 最近没有怎么读论文学新东西主要因为最近一直在写毕业论文。好消息是这周已经把毕业论文初稿基本写完了，差不多下周就能完成毕业论文了。论文写的差不多的话下个月我准备每周按时更新博客啦，同时下周5.1也是打算先回个家，然后回学校喽！所以本周我就水一篇我之前写的算法题-n皇后问题的题解。

问题介绍

n−皇后问题是指将 n 个皇后放在 n×n 的国际象棋棋盘上，使得皇后不能相互攻击到，即任意两个皇后都不能处于同一行、同一列或同一斜线上。

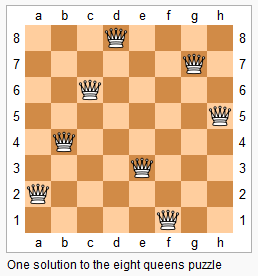
现在给定整数 n，请你输出所有的满足条件的棋子摆法。

输入格式

共一行，包含整数 n。

输出格式

每个解决方案占 n 行，每行输出一个长度为 n 的字符串，用来表示完整的棋盘状态。

其中 . 表示某一个位置的方格状态为空，Q 表示某一个位置的方格上摆着皇后。

每个方案输出完成后，输出一个空行。 注意：行末不能有多余空格。

输出方案的顺序任意，只要不重复且没有遗漏即可。

数据范围

1≤n≤9

输入样例：

plaintext
1
4

输出样例：

plaintext
1
2
3
4
5
6
7
8
9
.Q..
...Q
Q...
..Q.

..Q.
Q...
...Q
.Q..

题解

题目种最重要的信息：任意两个皇后都不能处于同一行、同一列或同一斜线上

这道题该如何思考呢？

本质上，n 皇后问题是一个典型的回溯问题：

  • 每一行放一个皇后，在放之前判断当前位置是否被其他皇后攻击（即列、对角线、反对角线有没有冲突）。
  • 如果当前位置安全，放置皇后，并递归到下一行。
  • 如果递归返回（回溯），需要撤销当前放置，继续尝试其他位置。

我感觉这个代码写n-皇后问题实在是太简洁了，所以忍不住让人分享出来。

建议结合代码和这段描述一起看哦~

棋盘表示：

  • 使用一个二维字符数组 s[N][N] 表示棋盘。
  • 'Q' 表示皇后，'.' 表示空位。

辅助数组：

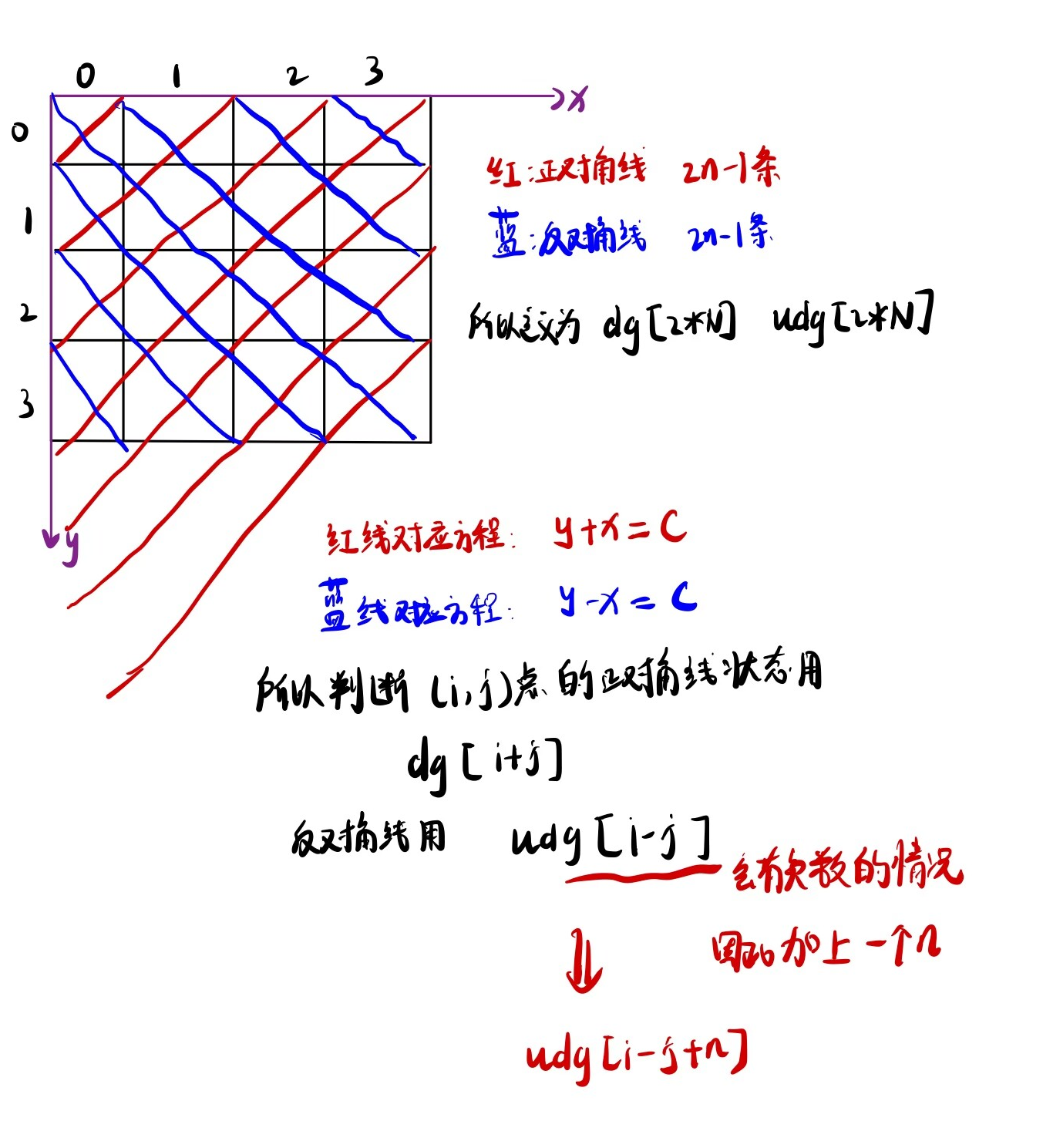
  • col[i]：记录第 i 列是否有皇后。
  • dg[i]：记录正对角线（↙）是否有皇后。编号方法是 行号 + 列号。
  • udg[i]：记录反对角线（↘）是否有皇后。编号方法是 行号 - 列号 + n（加 n 保证下标非负）。

可能这里你会不明白为什么dg和udg数组大小定义2N?还有为什么编号方法是这样？

DFS递归：

  • dfs(level) 表示当前正在处理第 level 行。
  • 如果 level == n，说明所有行都放置完毕，输出当前棋盘。
  • 否则，遍历当前行的每一列，尝试放置皇后。

完整代码：

cpp
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include <iostream>
using namespace std;

const int N=10; // 棋盘大小最大设为10
char s[N][N]; //存储n*n棋盘
int col[N],dg[2*N],udg[2*N]; //存储 列、正对角线、反对角线的占用情况

int n;   // 棋盘大小

void dfs(int level)
{
    if(level==n)        // 成功放置 n 个皇后，输出棋盘
    {
        for(int i=0;i<n;i++)
            cout<<s[i]<<endl;
        cout<<endl;
        return;
    }
    
    // 尝试在当前行每一列放置皇后
    for(int i=0;i<n;i++)
    {
        if(!col[i]&&!dg[level+i]&&!udg[level-i+n])
        {
            // 当前格子安全
            s[level][i]='Q';
            col[i]=dg[level+i]=udg[level-i+n]=1;
            
            dfs(level+1); // 递归到下一行
            // 回溯：撤销当前放置
            s[level][i]='.';
            col[i]=dg[level+i]=udg[level-i+n]=0;
        }
    }
}

int main()
{
    cin>>n;  // 输入棋盘大小
    for(int i=0;i<n;i++)
        for(int j=0;j<n;j++)
            s[i][j]='.'; // 初始化棋盘为空位
    dfs(0);  // 从第 0 行开始搜索
    
    return 0;
}