机器学习(3):线性回归(上)

Linear Regression

线性回归主要用于解决回归问题，而上次介绍的KNN主要用于分类问题。线性回归同样思想简单并且实现容易（与其背后非常强的数学性质相关）,虽然线性回归非常简单，但它是许多强大的非线性模型的基础。无论是多项式回归、逻辑回归甚至是SVM，从某种程度上都可以理解是线性回归的一种拓展。同时线性回归得到的结果具有很好的可解释性。

什么是线性回归算法？

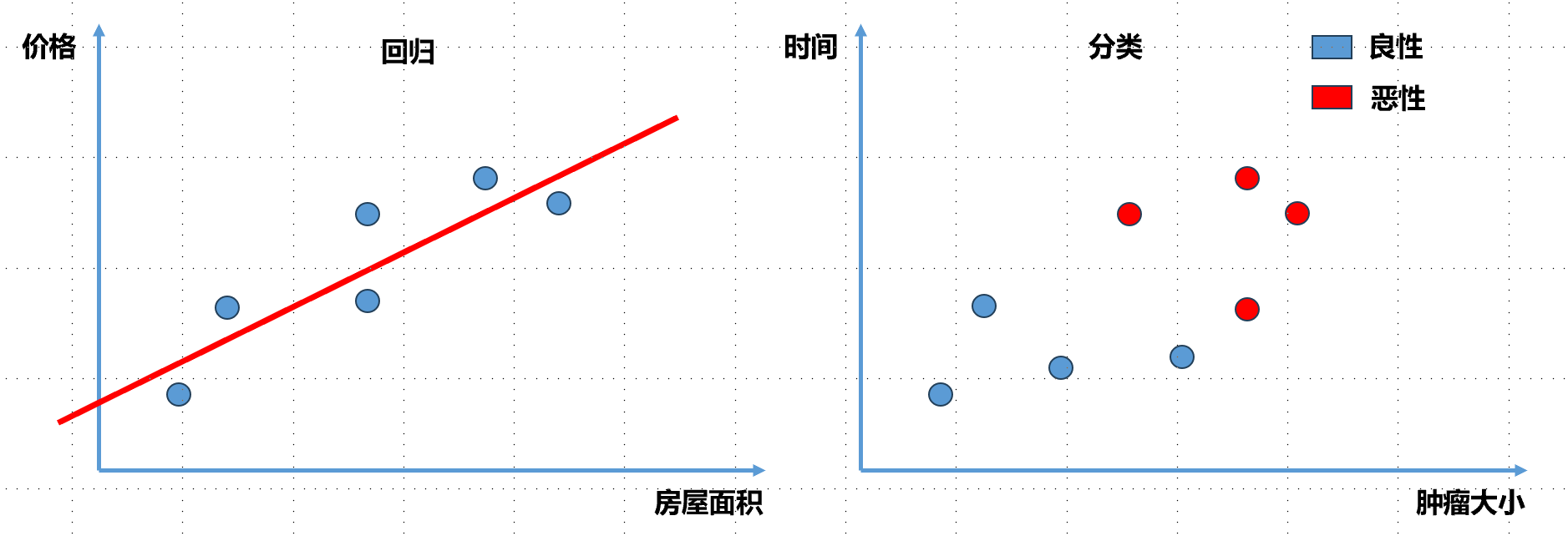
看下面图中每一个点表示一个数据，每个数据点有自己的房屋面积以及相应的价格。线性回归算法认为房屋面积和价格之间成一定的线性关系，随着房屋面积增大，价格也会线性增长。在这种假设下，我们在想能不能找到一条直线，最大程度的拟合样本特征和样本输出标记之间的关系

同时注意上一节的分类问题中数据点横轴肿瘤大小和纵轴时间都是样本特征，每一个点有两个样本特征，样本输出标记是由红色蓝色表示的。在左图回归的例子中，横轴房屋面积就是样本特征，而纵轴价格就是样本的输出标记。这主要是因为回归问题中真正要预测的是一个具体的数值，这个具体的数值是在一个连续的空间中而不是可以简单的用不同颜色代表不同类别。所以需要占用一个坐标轴位置。

上面例子中样本特征只有一个，被称为简单线性回归

对于简单线性回归，假设我们找到了最佳拟合的直线方程：
$$
y=ax+b
$$
对于每一个样本点$x^{(i)}$ ,根据我们的直线方程预测值为：
$$
\hat{y}^{(i)}=ax^{(i)}+b
$$
对于每一个样本点$x^{(i)}$ ，我们有一个真值$y^{(i)}$ ,为了寻找最佳拟合方程，我们希望$y^{(i)}$ 和$\hat{y}^{(i)}$ 的差距尽量小:

表达$y^{(i)}$ 和$\hat{y}^{(i)}$ 的差距：$y^{(i)}-\hat{y}^{(i)}$ 但是可能会出现一个+100 一个-100加起来为0，显然不合理，因此加上绝对值
$$
|y^{(i)}-\hat{y}^{(i)}|
$$
使用绝对值表示差异没有问题，但是后续用来计算$a,b$ 使用绝对值非常不方便，因此使用：
$$
(y^{(i)}-\hat{y}^{(i)})^2
$$
平方同样抵消了正负号，同时$y=x^2$函数连续处处可导，考虑所有的样本有：
$$
\sum^{m}{i=1}(y^{(i)}-\hat{y}^{(i)})^2
$$
因此目标：
$$
使\sum^{m}{i=1}(y^{(i)}-\hat{y}^{(i)})^2尽可能小\
代入\hat{y}^{(i)}=ax^{(i)}+b\
目标找到a,b使得\sum^{m}_{i=1}(y^{(i)}-ax^{(i)}-b)^2尽可能小
$$

这也是一类机器学习算法的基本思路：找到一些参数值，使得目标function 尽可能大或小

所谓建模的过程其实就是找到一个模型最大程度拟合我们的数据，在线性回归算法中这个模型就是一个方程，最大拟合数据本质就找到这样一个函数，这里叫损失函数Loss function，度量出模型没有拟合出样本的这一部分，有些算法可能度量拟合的程度，这种情况下称做效用函数(utility function).

不管哪个函数，机器学习都是先分析问题确定问题的损失函数或者效用函数，通过最优化损失函数或效用函数，获得机器学习模型。

几乎所有参数学习的算法都是这个套路，区别在于模型不同建立的目标函数不同，优化方式也是不同的。正是因为机器学习算法大部分都是这个思路，有一个学科最优化原理。

最小二乘法

上面将问题最终转化成一个最优化问题：
$$
目标:找到a,b使得\sum_{i=1}^{m}\underbrace{(y^{(i)}-ax^{(i)}-b)^2}{\text{J(a,b)}}尽可能小
$$
将里面式子记为$J(a,b)$ 因为$a,b$ 是未知数，此时转换为求改函数的最小值，通过求导极值为0.
$$
\frac{\partial J(a,b)}{\partial b}=\sum{i=1}^{m}2(y^{(i)}-ax^{(i)}-b)(-1)=0\
\sum_{i=1}^{m}(y^{(i)}-ax^{(i)}-b)=0\
\sum_{i=1}^{m}y^{(i)}-a\sum_{i=1}^{m}x^{(i)}-\sum_{i=1}^{m}b=0\
mb=\sum_{i=1}^{m}y^{(i)}-a\sum_{i=1}^{m}x^{(i)}\
b=\bar{y}-a\bar{x} \quad\quad(1)\
—————————-\
\frac{\partial J(a,b)}{\partial a}=\sum_{i=1}^{m}2(y^{(i)}-ax^{(i)}-b)(-x^{(i)})=0\
\sum_{i=1}^{m}(y^{(i)}-ax^{(i)}-b)x^{(i)}=0\
\sum_{i=1}^{m}(y^{(i)}-ax^{(i)}-\bar{y}+a\bar{x})x^{(i)}=0 \quad \quad代入(1)式\
\sum_{i=1}^{m}(x^{(i)}y^{(i)}-a(x^{(i)})^2-x^{(i)}\bar{y}+a\bar{x}x^{(i)})=0 \
\sum_{i=1}^{m}(x^{(i)}y^{(i)}-x^{(i)}\bar{y}-a(x^{(i)})^2+a\bar{x}x^{(i)})=0 \
\sum_{i=1}^{m}(x^{(i)}y^{(i)}-x^{(i)}\bar{y})-a\sum_{i=1}^{m}((x^{(i)})^2-\bar{x}x^{(i)})=0 \
a=\frac{\sum_{i=1}^{m}(x^{(i)}y^{(i)}-x^{(i)}\bar{y})}{\sum_{i=1}^{m}((x^{(i)})^2-\bar{x}x^{(i)})}\
$$

对$a$的形式进一步简化：
$$
\sum_{i=1}^{m}x^{(i)}\bar{y}=\bar{y}\sum_{i=1}^{m}x^{(i)}=m\bar{y}\bar{x}=\bar{x}\sum_{i=1}^{m}y^{(i)}=\sum_{i=1}^{m}\bar{x}y^{(i)}=\sum_{i=1}^{m}\bar{x}\bar{y}\
a=\frac{\sum_{i=1}^{m}(x^{(i)}y^{(i)}-x^{(i)}\bar{y}-\bar{x}y^{(i)}+\bar{x}\bar{y})}{\sum_{i=1}^{m}((x^{(i)})^2-\bar{x}x^{(i)}-\bar{x}x^{(i)}+\bar{x}^2)}\
a=\frac{\sum_{i=1}^{m}(x^{(i)}-\bar{x})(y^{(i)}-\bar{y})}{\sum_{i=1}^{m}(x^{(i)}-\bar{x})^2}\quad\quad(2)\
$$

实现Simple Linear Regression

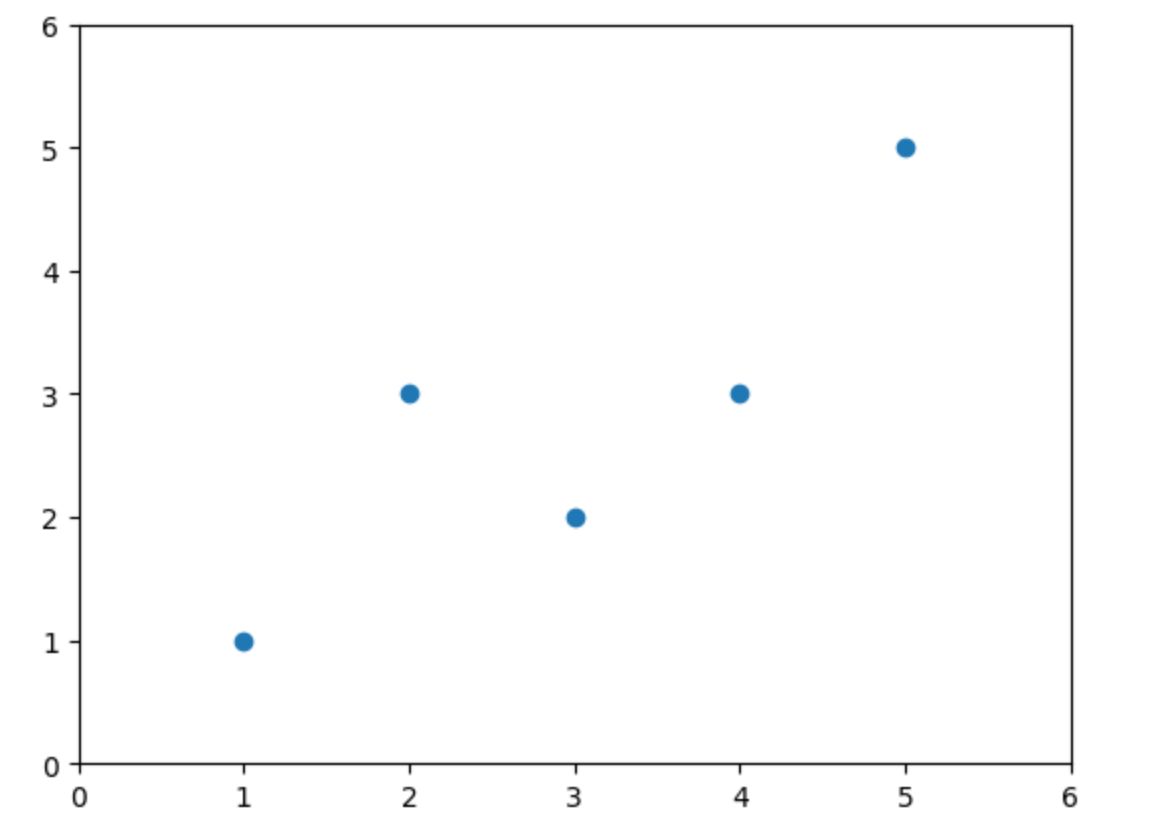
假如我们有如下数据点：

然后根据上面推出的式(1)和式(2)编程求解$a,b$ 的值：

x_mean, y_mean = np.mean(x), np.mean(y)
numerator = 0.0
denominator = 0.0
for x_i, y_i in zip(x,y):
    numerator += (x_i-x_mean)*(y_i-y_mean)
    denominator += (x_i-x_mean)**2
a = numerator/denominator
b = y_mean - a*x_mean

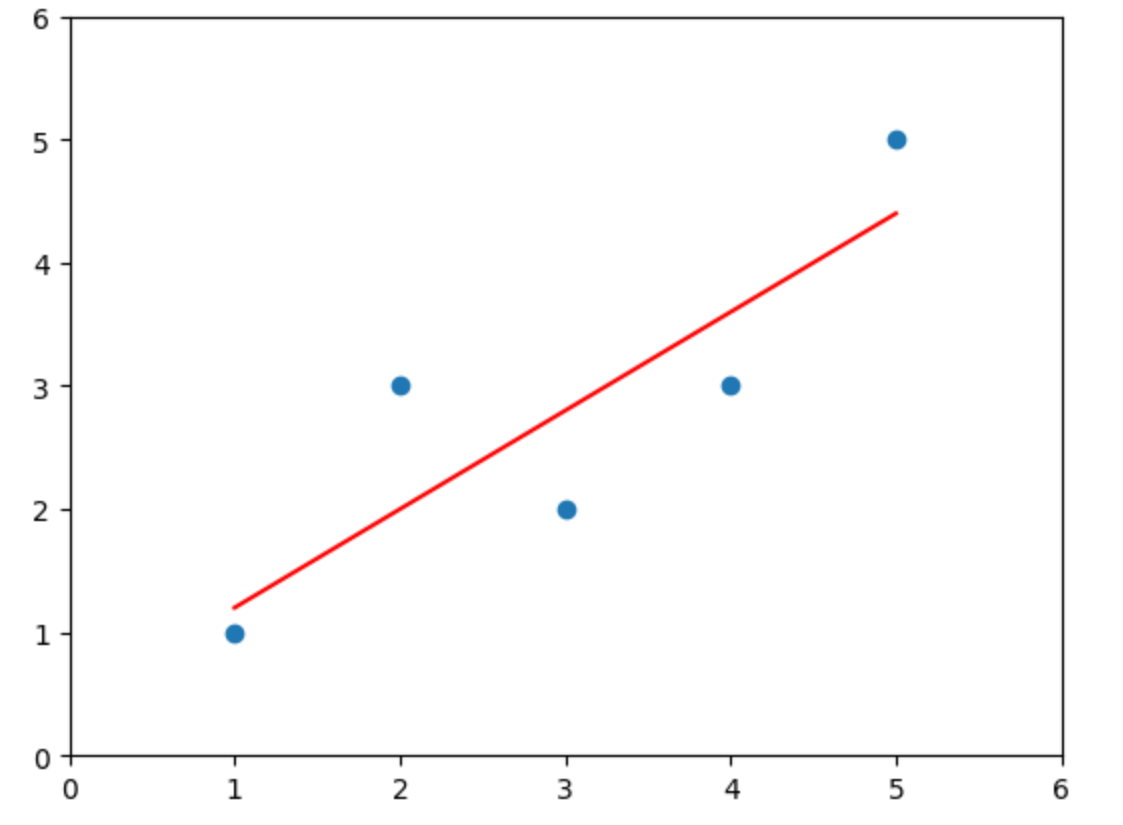
针对上述5个数据点我求的$a,b$的值分别为0.8和0.4 ，然后绘制到图中：

对于一个新来的数据点比如x=6,我们带入公式可得此时$y=0.8*6+0.4=5.2$

封装自己的算法

import numpy as np

class SimpleLinearRegression1:

    def __init__(self):
        self.a_ = None
        self.b_ = None
    
    def fit(self, x_train, y_train):
        assert x_train.ndim==1,\
        "Simple Linear Regression  can only slove single feature training data"
        assert len(x_train) == len(y_train),\
        "the size of x_trian must be equle to the size of y_train"

        x_mean, y_mean = np.mean(x_train), np.mean(y_train)
        numerator = 0.0
        denominator = 0.0
        for x_i, y_i in zip(x_train, y_train):
            numerator += (x_i-x_mean)*(y_i-y_mean)
            denominator += (x_i-x_mean)**2
        self.a_ = numerator/denominator
        self.b_ = y_mean - self.a_*x_mean
        return self

    def predict(self, x_predict):
        assert x_predict.ndim==1,\
        "Simple Linear Regression  can only slove single feature training data"
        assert self.a_ is not None and self.b_ is not None ,\
        "must fit before predict"

        return np.array([self._predict(x) for x in x_predict])
    
    def _predcit(self, x_single):
        return self.a_*x_single + self.b_
    
    def __repr__(self):
        return "SimpleLinearRegression1()"

向量化

上面封装算法时采用for循环的方法，效率很低，而上面求导$a$ 的形式时做了变换使其便于我们后续做向量化操作

import numpy as np

class SimpleLinearRegression2:

    def __init__(self):
        self.a_ = None
        self.b_ = None
    
    def fit(self, x_train, y_train):
        assert x_train.ndim==1,\
        "Simple Linear Regression  can only slove single feature training data"
        assert len(x_train) == len(y_train),\
        "the size of x_trian must be equle to the size of y_train"

        x_mean, y_mean = np.mean(x_train), np.mean(y_train)
        numerator = (x_train-x_mean).dot(y_train-y_mean)  # 用点乘
        denominator = (x_train-x_mean).dot(x_train-x_mean)
 
        self.a_ = numerator/denominator
        self.b_ = y_mean - self.a_*x_mean
        return self

    def predict(self, x_predict):
        assert x_predict.ndim==1,\
        "Simple Linear Regression  can only slove single feature training data"
        assert self.a_ is not None and self.b_ is not None ,\
        "must fit before predict"

        return np.array([self._predict(x) for x in x_predict])
    
    def _predcit(self, x_single):
        return self.a_*x_single + self.b_
    
    def __repr__(self):
        return "SimpleLinearRegression2()"

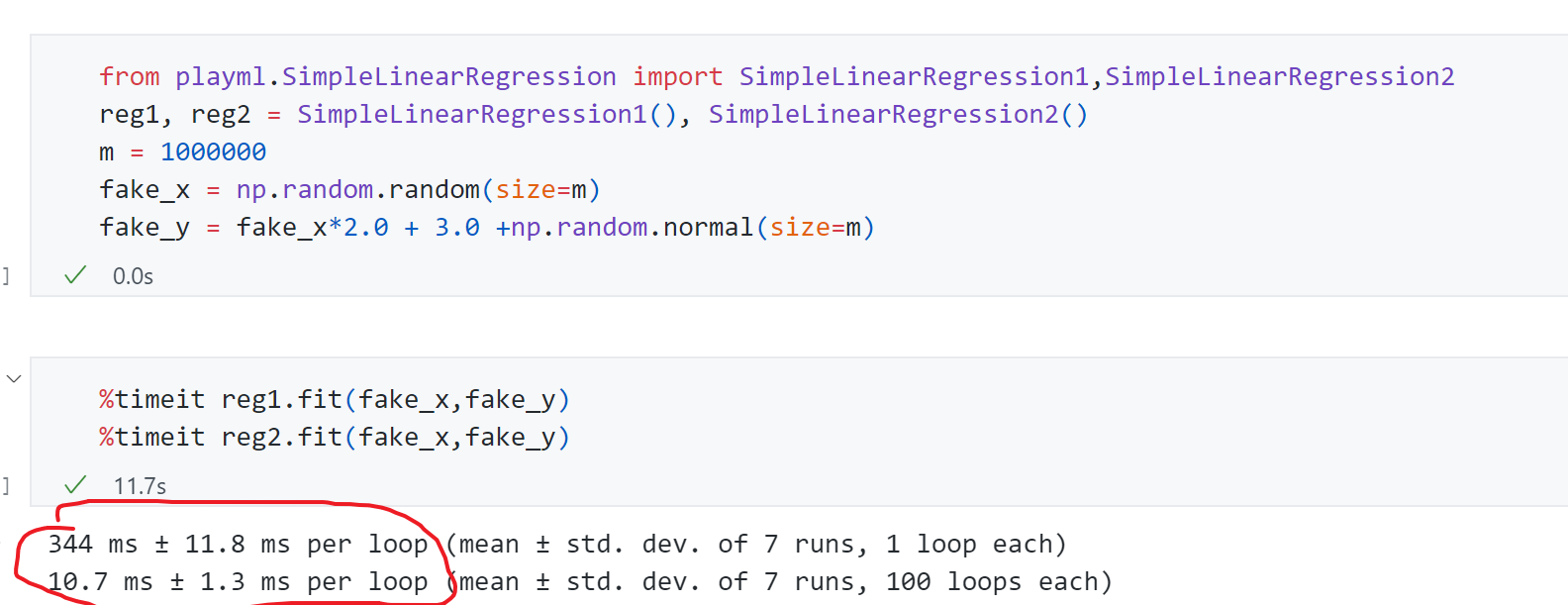
性能测试结果如下：

第一个for循环版本平均用时344ms，第二个向量化版本平均用时11ms，性能提升了30倍左右。

回归算法评价指标

前面训练目标主要是针对训练集而言：
$$
目标:找到a,b使得\sum_{i=1}^{m}(y^{(i)}{train}-\hat{y}{train}^{(i)})^2尽可能小
$$
然后基于训练得到的模型得到：
$$
\hat{y}{test}^{(i)}=ax^{(i)}{test}+b\
衡量标准:\sum_{i=1}^{m}(y^{(i)}{test}-\hat{y}{test}^{(i)})^2
$$
但有个存在的问题就是这个衡量标准是跟m相关的，假如一个A算法得到误差是1000，另一个B算法是800，就能说明B算法好吗？显然不是，假如A算法是1000个样本误差和为1000，而B算法是10个样本误差和为800，显然A算法更好，因此对该指标很自然的一个改进就是：
$$
\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}{test}-\hat{y}{test}^{(i)})^2\
均方误差MSE(Mean \quad Squared \quad Error)
$$
但这个衡量标准还有一个小问题就是量纲上问题，比如如果$y$ 单位为万元，这个衡量标准就是万元的平方，这个量纲有时候可能会带来麻烦，所以一个简单的改写方式就是将MSE的值开一个根号：
$$
\sqrt{\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}{test}-\hat{y}{test}^{(i)})^2}\
均方根误差RMSE(Root\quad Mean \quad Squared \quad Error)
$$
另外一个评测标准：
$$
\frac{1}{m}\sum_{i=1}^{m}|y^{(i)}{test}-\hat{y}{test}^{(i)}|\
平均绝对误差MAE( Mean \quad Absolute \quad Error)
$$
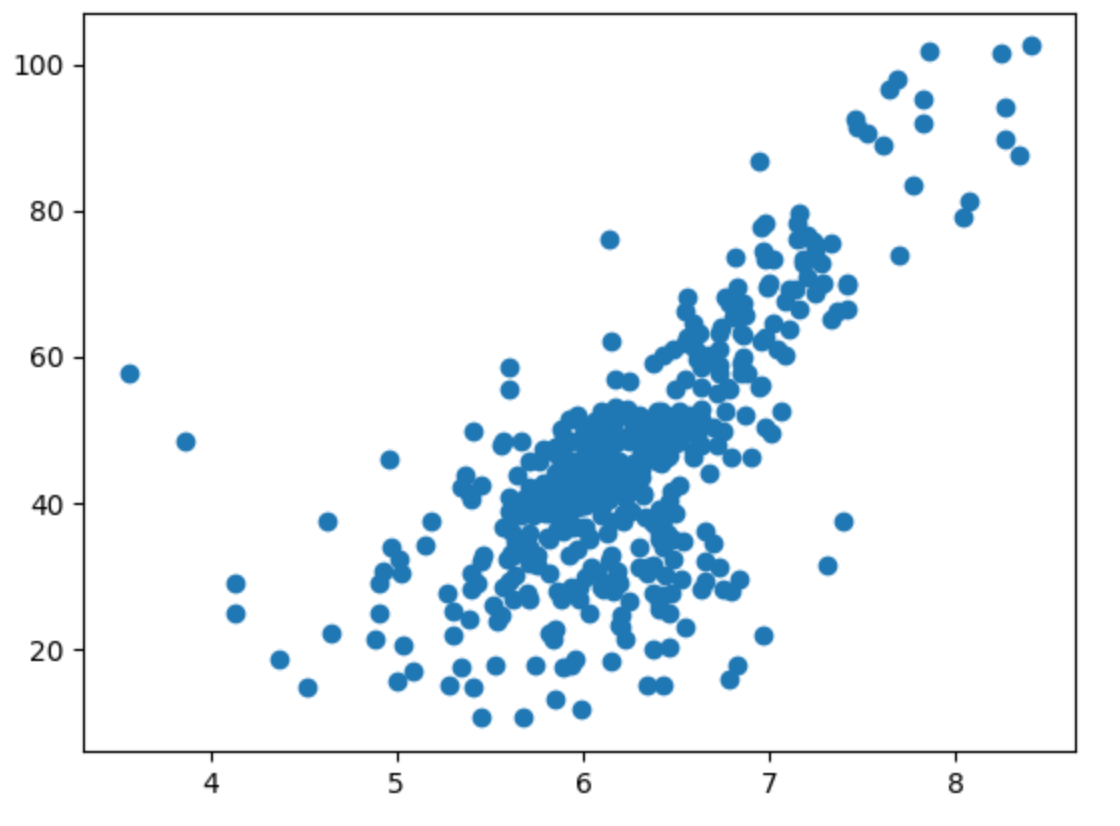
具体实现选用Boston房产数据：

其中x轴代表每个房产中平均的房间数量，y轴代表房产价格(万美元)

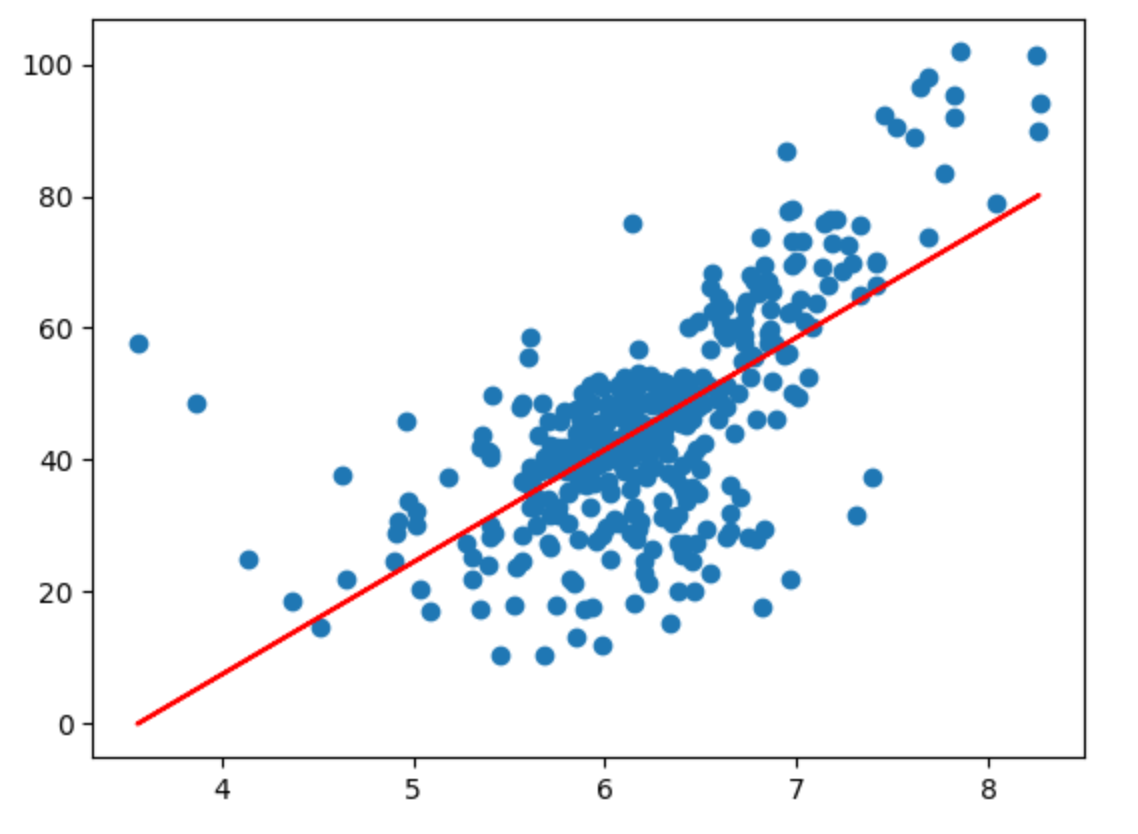
然后使用封装的代码拟合求解：

from playml.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(x, y, seed=666)

from playml.SimpleLinearRegression import SimpleLinearRegression2
reg = SimpleLinearRegression2()
reg.fit(X_train, y_train)

plt.scatter(X_train, y_train)
plt.plot(X_train,reg.predict(X_train),"r")
plt.show()

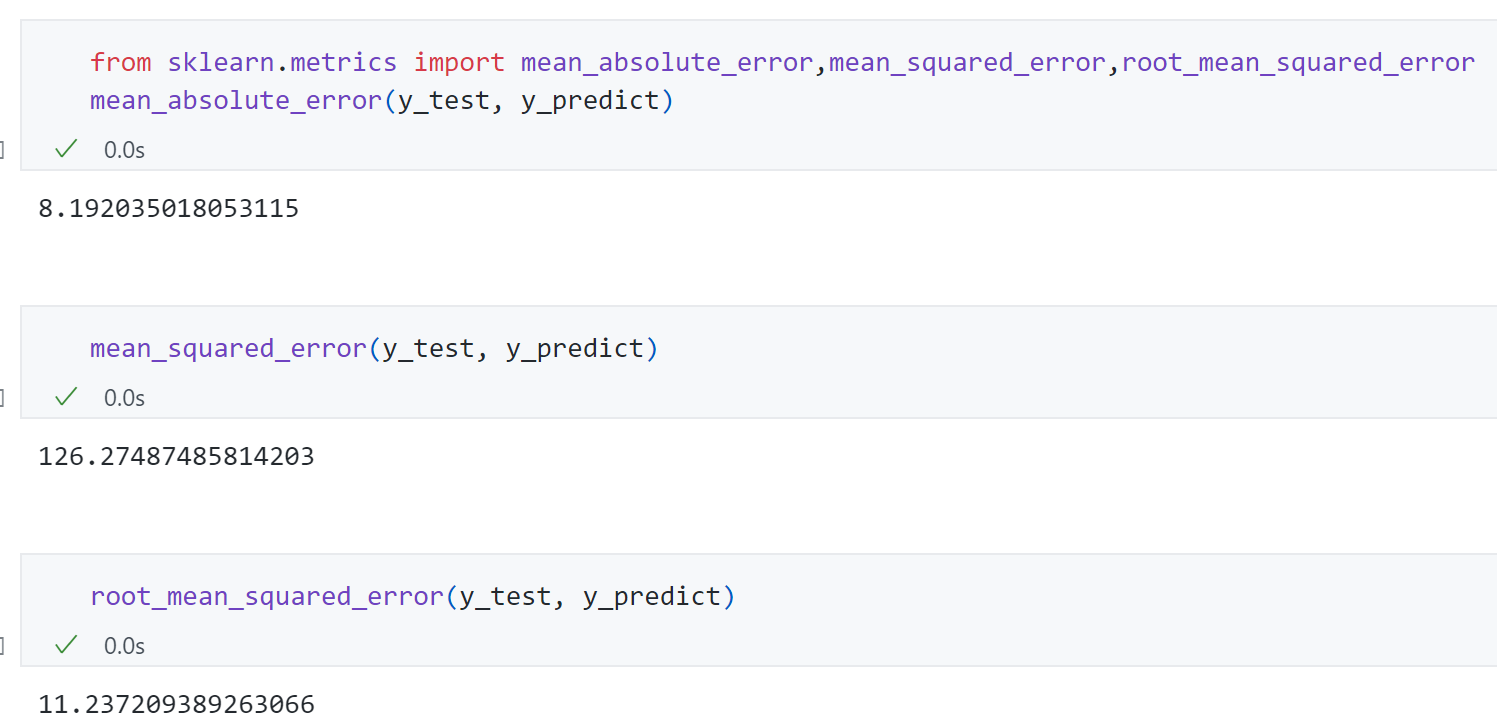
计算MSE,RMSE,MAE三个指标：

1
2
3

mse_test = np.sum((y_predict-y_test)**2)/len(y_test)
rmse = np.sqrt(mse_test)
mae_test = np.sum(np.abs(y_predict-y_test))/len(y_test)

求得MSE，RMSE,MAE的结果分别为126.27487485814203，11.237209389263066，8.192035018053115.

封装指标：

def mean_squared_error(y_true, y_predict):
    assert len(y_true) == len(y_predict),\
    "the size of y_true must be equal to the size of y_predict"
    return np.sum((y_predict-y_true)**2)/len(y_true)

def root_mean_squared_error(y_true, y_predict):

    return np.sqrt(mean_squared_error(y_true, y_predict))

def mean_absolute_error(y_true, y_predict):
    assert len(y_true) == len(y_predict),\
    "the size of y_true must be equal to the size of y_predict"
    return np.sum(np.abs(y_predict-y_true))/len(y_true)

用Scikit-learn中的函数求解：

发现数值结果同我们上面计算的一样.

RMSE VS MAE

从上面结果可以发现MAE结果8.19比RMSE的结果11.23略小，为什么呢？通过RMSE的算式就可以发现，RMSE是先平方在开方，如果错误值很大比如100经过平方就扩大到了10000，即RMSE有放大我们样本中预测结果和真实结果之间较大的那个差距的趋势，而MAE直接反映的样本的预测结果和真实结果之间的差距，没有平方操作。也正是如此，从某种程度来讲，我们尽量让RMSE这个值更加小相对来说意义更大，这背后意味着整个样本错误中那个最大的错误值相应的比较小。