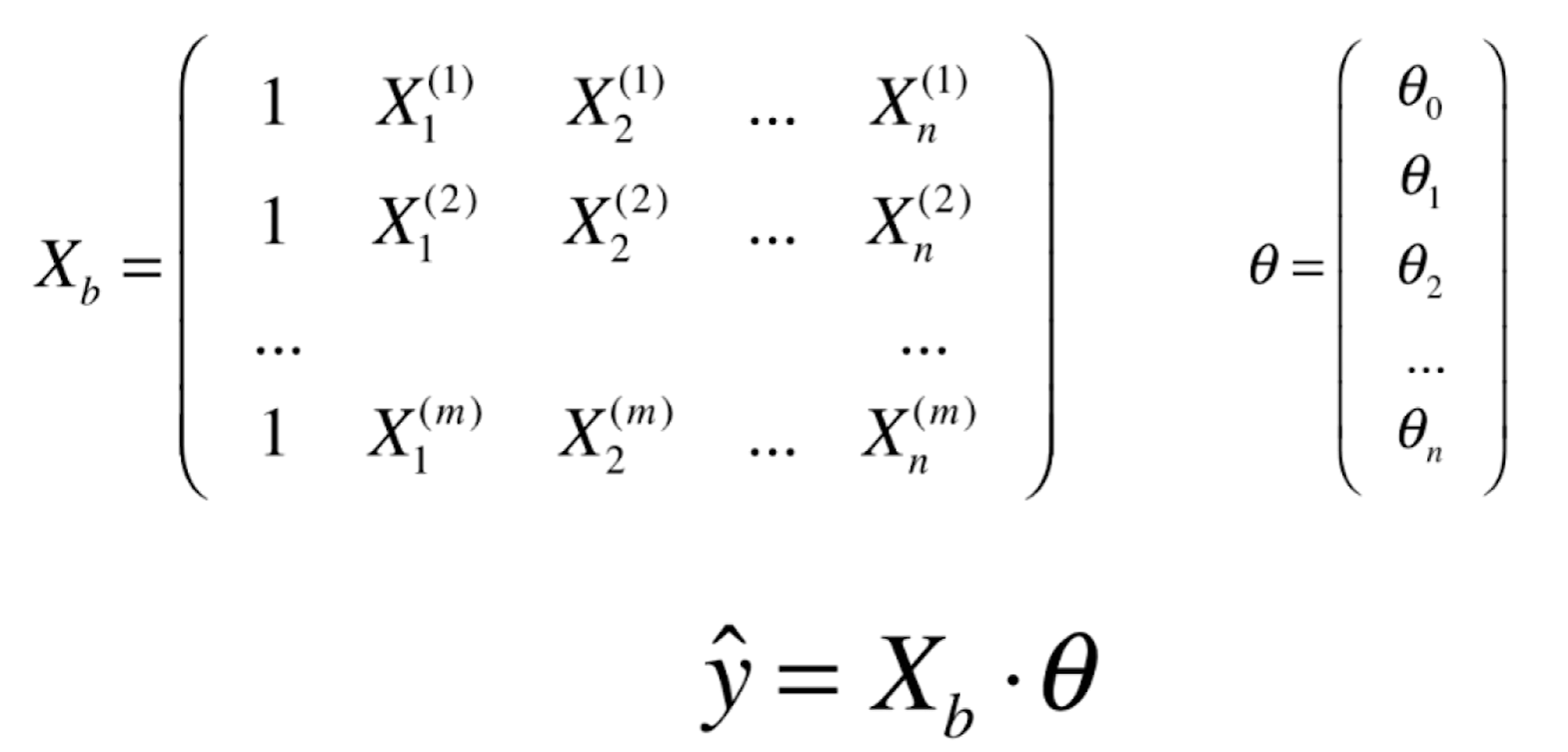Linear Regression
上篇文章中介绍了评价回归算法优劣的三个指标MSE、RMSE、MAE ,但是这三个指标还有它本身的问题 。回想分类问题中评价指标采用分类准确度:1最好,0最差。即使分类问题不同 ,我们也可以很容易比较它们之间的优劣 ,但是RMSE和MAE没有这样的性质。比如预测房产数据最后得到RMSE是5万元,而预测学生成绩最终结果是10分,在这种情况下我们的算法是作用在预测房产上好呢还是预测学生成绩好呢?显然是无法判断的,因为这个5 万元和10分 对应不同种类的东西,我们无法直接比较,这就是直接使用RMSE和MAE的局限性 。
R Squared
为了解决上述问题,我们可以采用一个新的指标R 2 R^2 R 2 R Squared :
R 2 = 1 − S S r e s i d u a l S S t o t a l R 2 = 1 − ∑ i ( y ^ ( i ) − y ( i ) ) 2 ∑ i ( y ˉ ( i ) − y ( i ) ) 2 R 2 = 1 − ∑ i ( y ^ ( i ) − y ( i ) ) 2 / m ∑ i ( y ˉ ( i ) − y ( i ) ) 2 / m R 2 = 1 − M S E ( y , y ^ ) V a r ( y ) R^2=1-\frac{SS_{residual}}{SS_{total}}\\
R^2=1-\frac{\sum_{i}(\hat{y}^{(i)}-y^{(i)})^2}{\sum_{i}(\bar{y}^{(i)}-y^{(i)})^2}\\
R^2=1-\frac{\sum_{i}(\hat{y}^{(i)}-y^{(i)})^2/m}{\sum_{i}(\bar{y}^{(i)}-y^{(i)})^2/m}\\
R^2=1-\frac{MSE(y,\hat{y})}{Var(y)}
R 2 = 1 − S S t o t a l S S res i d u a l R 2 = 1 − ∑ i ( y ˉ ( i ) − y ( i ) ) 2 ∑ i ( y ^ ( i ) − y ( i ) ) 2 R 2 = 1 − ∑ i ( y ˉ ( i ) − y ( i ) ) 2 / m ∑ i ( y ^ ( i ) − y ( i ) ) 2 / m R 2 = 1 − Va r ( y ) MSE ( y , y ^ )
其中S S r e s i d u a l SS_{residual} S S res i d u a l S S t o t a l SS_{total} S S t o t a l
观察上面式子,S S r e s i d u a l SS_{residual} S S res i d u a l 模型预测产生的错误 ,S S t o t a l SS_{total} S S t o t a l y = y ˉ y=\bar{y} y = y ˉ y ˉ \bar{y} y ˉ y = y ˉ y=\bar{y} y = y ˉ Baseline model )
可以想象的是这个Baseline Model 的错误是比较多的,因为完全不考虑x,所有结果预测为均值,反之我们预测的错误相应是比较少的,因为它充分考虑x和y之间的关系,那么基于此我们可以这样理解R 2 R^2 R 2
这个式子描述的是我们使用Baseline 这个模型预测会产生非常多的错误,而使用我们的模型预测相应的也会产生一些错误,但同时也会减少一些错误,所有用1减去我们模型预测产生的错误除以Baseline Model预测产生的错误,最后的结果相当于衡量了我们的模型拟合住的这些数据的地方 ,相当于我们的模型没有产生错误的相应的那个指标。
R 2 < = 1 R^2<=1 R 2 <= 1 R 2 R^2 R 2 R 2 R^2 R 2 当我们的模型等于基准模型时,R 2 R^2 R 2
如果R 2 < 0 R^2<0 R 2 < 0
代码实现:
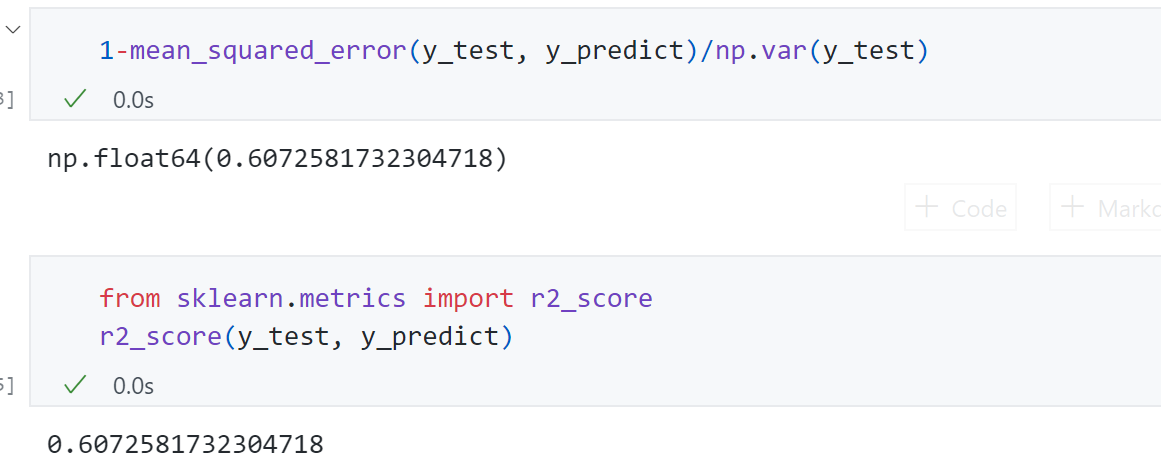
1 2 r_squared = 1 -mean_squared_error(y_test, y_predict)/np.var(y_test)
使用我们自己的实现与 scikit-learn中封装的r2_score函数得到的结果一致:
多元线性回归
上一篇主要讲的是简单线性回归问题,即假设我们的样本只有一个特征值。但是在真实世界中通常一个样本是有多个特征值的 ,甚至成千上万个特征值,针对这样的样本我们依然可以使用线性回归的思路来解决,这种问题通常称之为多元线性回归 。
多元线性回归的目标:
目标 : 找到 θ 0 , θ 1 , θ 2 , . . θ n , 使得 ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 尽可能小 θ = ( θ 0 , θ 1 , θ 2 , . . θ n ) T y ^ ( i ) = θ 0 X 0 ( i ) + θ 1 X 1 ( i ) + θ 2 X 2 ( i ) + . . . + θ n X n ( i ) , X 0 ( i ) ≡ 1 X ( i ) = ( X 0 ( i ) , X 1 ( i ) , X 2 ( i ) , . . , X n ( i ) ) y ( i ) = X ( i ) . θ 目标:找到\theta_0,\theta_1,\theta_2,..\theta_n,使得\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2尽可能小\\
\theta=(\theta_0,\theta_1,\theta_2,..\theta_n)^T\\
\hat{y}^{(i)}=\theta_0X_0^{(i)}+\theta_1X_1^{(i)}+\theta_2X_2^{(i)}+...+\theta_nX_n^{(i)},X_0^{(i)}\equiv1\\
X^{(i)}=(X_0^{(i)},X_1^{(i)},X_2^{(i)},..,X_n^{(i)})\\
y^{(i)}=X^{(i)}.\theta
目标 : 找到 θ 0 , θ 1 , θ 2 , .. θ n , 使得 i = 1 ∑ m ( y ( i ) − y ^ ( i ) ) 2 尽可能小 θ = ( θ 0 , θ 1 , θ 2 , .. θ n ) T y ^ ( i ) = θ 0 X 0 ( i ) + θ 1 X 1 ( i ) + θ 2 X 2 ( i ) + ... + θ n X n ( i ) , X 0 ( i ) ≡ 1 X ( i ) = ( X 0 ( i ) , X 1 ( i ) , X 2 ( i ) , .. , X n ( i ) ) y ( i ) = X ( i ) . θ
拓展到每个样本上:
对我们的目标还可以进一步向量化:
目标 : 找到 θ 0 , θ 1 , θ 2 , . . θ n , 使得 ∑ i = 1 m ( y ( i ) − y ^ ( i ) ) 2 尽可能小 目标 : 使 ( y − X b . θ ) T ( y − X b . θ ) 尽可能小 目标:找到\theta_0,\theta_1,\theta_2,..\theta_n,使得\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2尽可能小\\
目标:使(y-X_b.\theta)^T(y-X_b.\theta)尽可能小
目标 : 找到 θ 0 , θ 1 , θ 2 , .. θ n , 使得 i = 1 ∑ m ( y ( i ) − y ^ ( i ) ) 2 尽可能小 目标 : 使 ( y − X b . θ ) T ( y − X b . θ ) 尽可能小
对矩阵求导运算:
θ = ( X b T X b ) − 1 X b T y \theta = (X^T_bX_b)^{-1}X^T_by
θ = ( X b T X b ) − 1 X b T y
这个式子也被成为多元线性回归的正规方程解(Normal Equation ).这个式子问题就是时间复杂度高O ( n 3 ) ( 优化 O ( n 2.4 ) ) O(n^3)(优化O(n^{2.4})) O ( n 3 ) ( 优化 O ( n 2.4 ))
优点就是我们不要对数据进行归一化处理,因为通过数学分析得到最后的θ \theta θ θ \theta θ
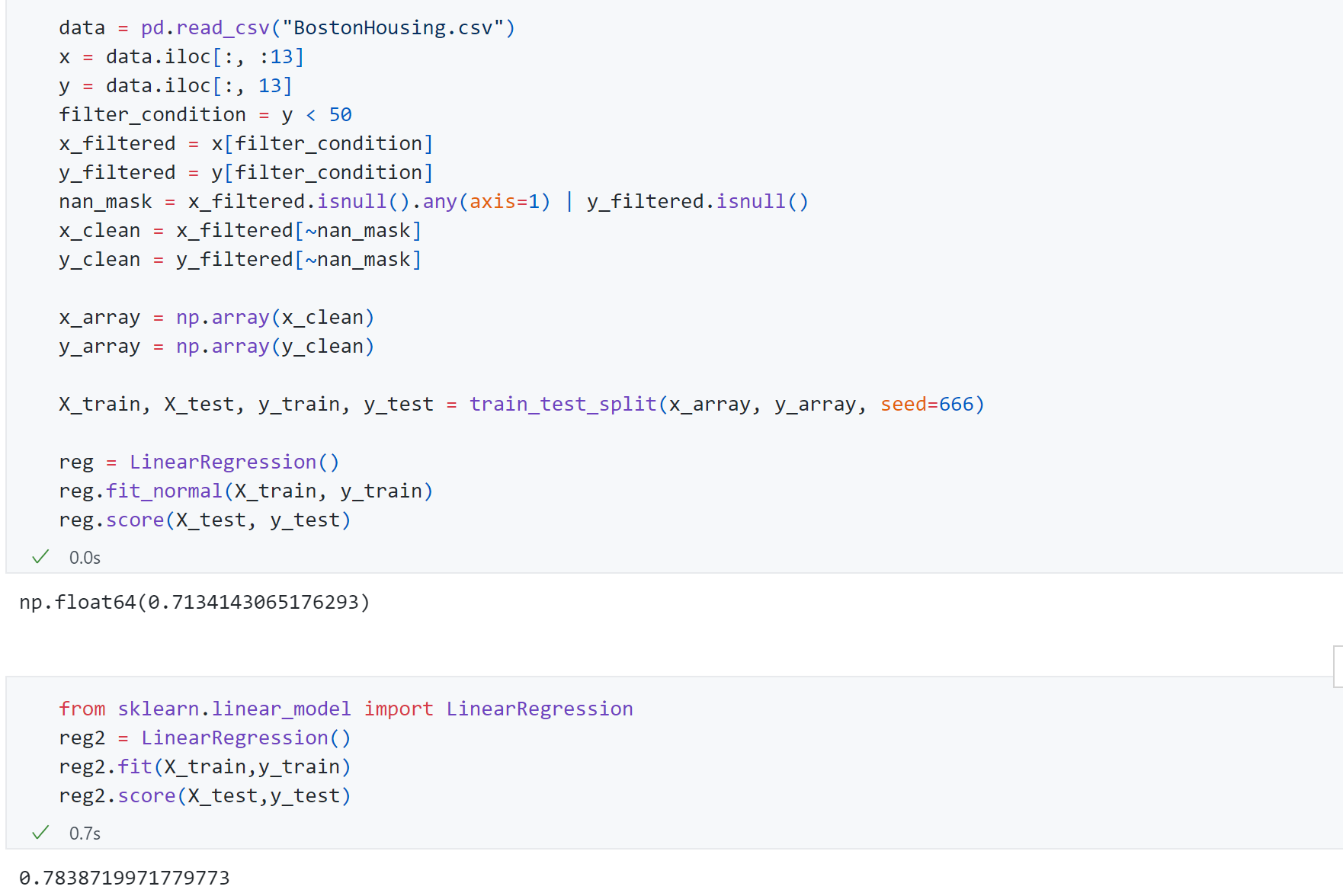
实现多元线性回归
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 import numpy as npfrom .metrics import r2_scoreclass LinearRegression : def __init__ (self ): self .coef_ = None self .interception_ = None self ._theta = None def fit_normal (self, X_train, y_train ): assert X_train.shape[0 ] == y_train.shape[0 ],\ "the size of X_train must be equal to the size of y_train" X_b = np.hstack([np.ones((len (X_train),1 )),X_train]) self ._theta = np.linalg.inv(X_b.T.dot(X_b)).dot(X_b.T).dot(y_train) self .interception_ = self ._theta[0 ] self .coef_ = self ._theta[1 :] return self def predict (self, X_predict ): assert self .coef_ is not None and self .interception_ is not None ,\ "must fit before predict!" assert X_predict.shape[1 ] == len (self .coef_),\ "the feature number of X_predict must be equal to X_train" X_b = np.hstack([np.ones((len (X_predict),1 )),X_predict]) return X_b.dot(self ._theta) def score (self, X_test,y_test ): y_predcit = self .predict(X_test) return r2_score(y_test, y_predcit) def __repr__ (self ): return "LinearRegression()"
测试性能得到R 2 R^2 R 2 0.71 (我们封装的方法)和0.78 (scikit-learn中的方法)
线性回归的可解释性
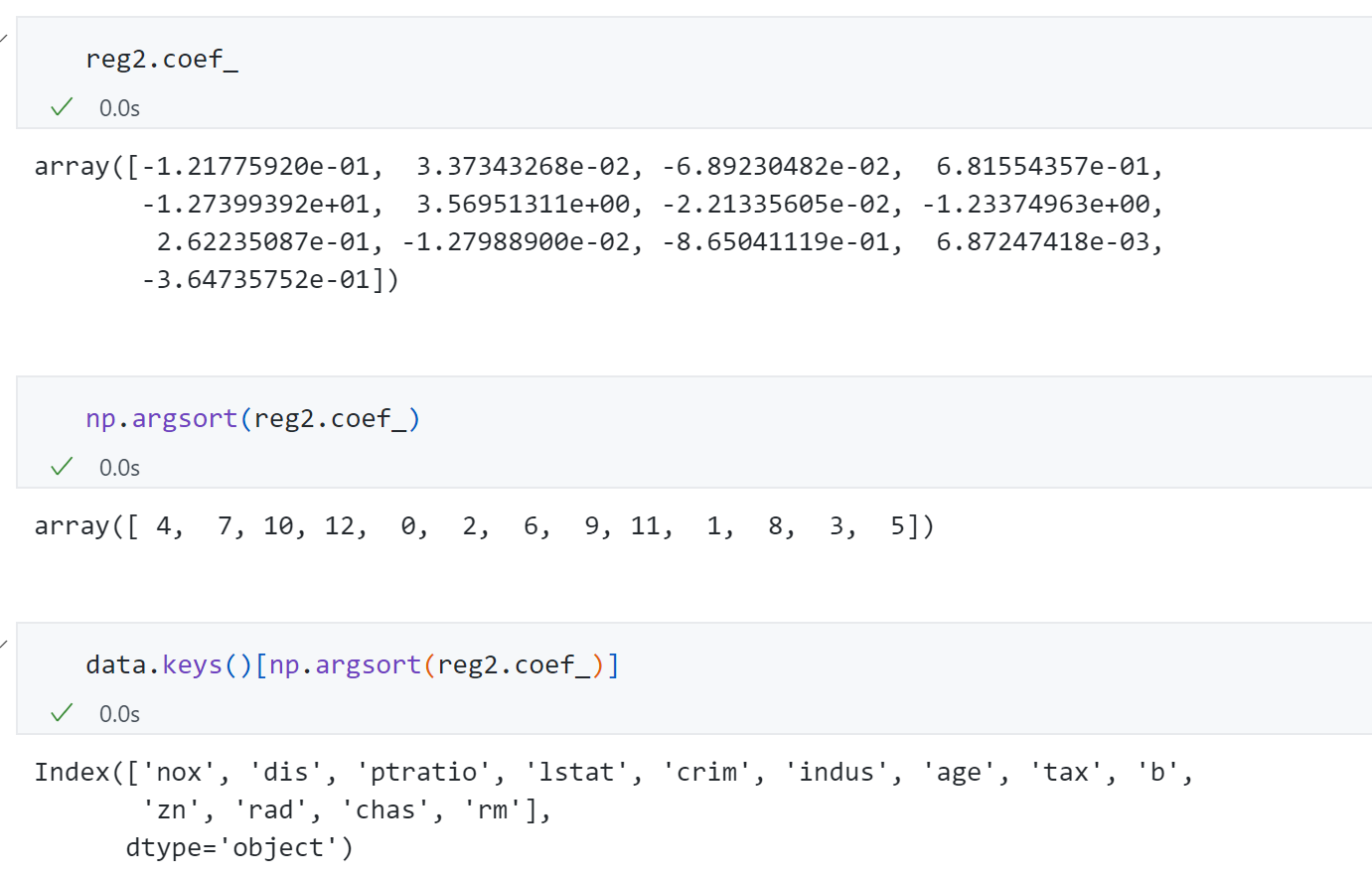
将我们的回归结果系数从小到大进行排序取出Boston housing数据中对应的feature_name:
观察发现"rm " 和 ‘chas ’ 系数 最大,与房价最为正相关,而其中’rm ’ 代表的平均房间数量 ,而’chas ’ 表示房子是否靠近河边 ,那么我们可以理解 房间数量越多,房价越高;房间临近河,房价越高。反观‘Nox ’最负相关,代表的是一氧化氮浓度,说明 一氧化氮浓度越高,房价越低。 这就说明线性回归对我们的数据有可解释性。
总结
线性回归 是一种典型的参数学习 算法,对比KNN是一种典型的非参数学习算法。同时线性回归只能解决回归问题 ,而KNN既可以解决回归问题也可以解决分类问题 。但线性回归是基础比如逻辑回归,同时线性回归具有很强的解释性,是个“白盒子算法 ”。最后本次主要介绍了线性回归的正规方程解法,这种解法数学原理简单但是时间复杂度高,如果样本数量很大就很难应用,同时对与许多复杂的机器学习算法它是没有正规方程解 的,这也引出了后续著名的梯度下降法-Gradient Descent .