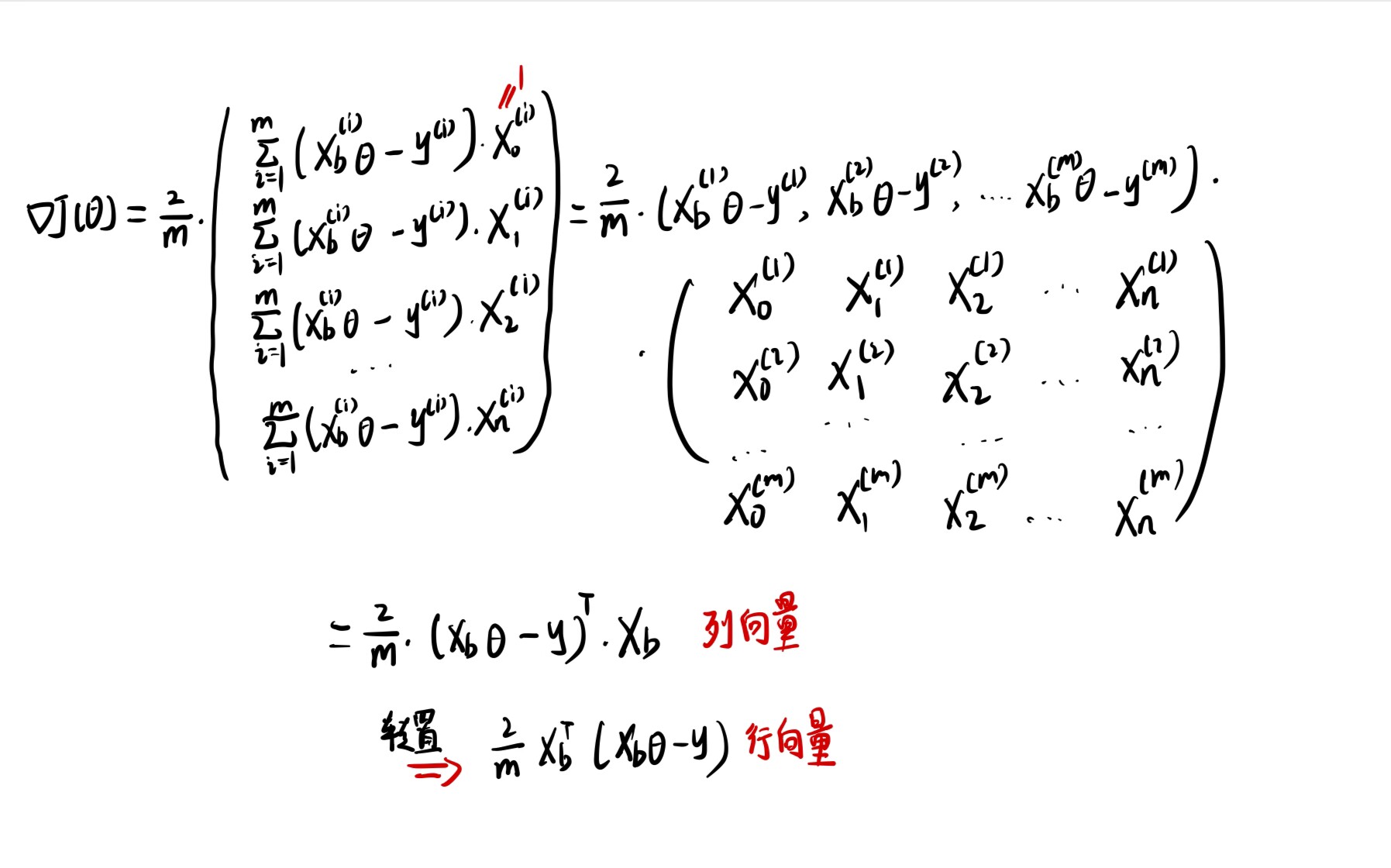Gradient Descent

梯度下降法跟前面文章中提到的KNN算法和线性回归算法不同，梯度下降法本身不是一个机器学习算法，它既不是在做监督学习也不是在做非监督学习，它不能用于解决回归问题或者分类问题。它是一种基于搜索的最优化方法，主要作用是优化一个目标函数比如最小化损失函数，反之梯度上升法用来最大化一个效用函数。

上篇线性回归中最小化损失函数最终得到了参数的数学解析形式，但很多机器学习模型是求不到这样的数学解的，那么基于这样的模型就需要使用一种基于搜索的策略来找到这个最优解。而梯度下降法就是机器学习领域最小化一个损失函数的最常用方法。

图解

依旧看下面一个二维平面，xx 轴代表参数θ\theta 的取值，yy 轴代表损失函数取值。最小化损失函数在这个平面中相当于找到合适的参数使得损失函数取得最小值，为了可视化方便此时选用二维平面相当于只有一个参数，扩展到高维同理。

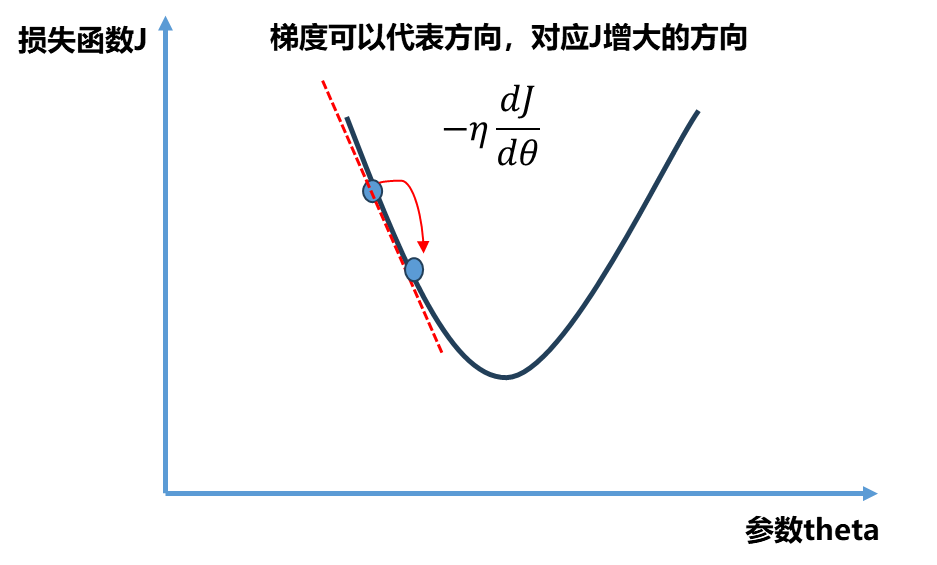
image-20250921224529281

其中η\eta 称为学习率(learning rate),是梯度下降法的一个超参数。η\eta 的取值影响获得最优解的速度，取值不合适甚至得不到最优解.

image-20250921225108749

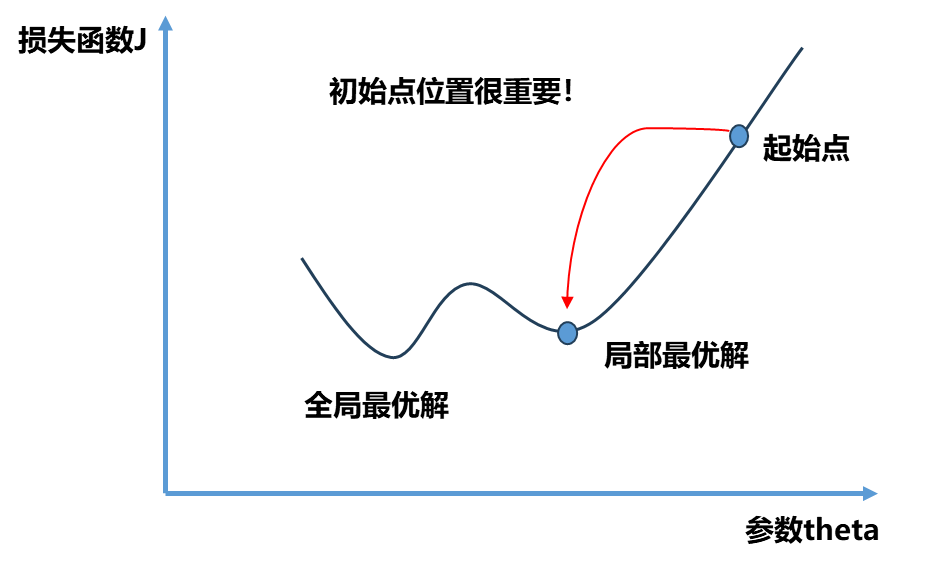
不是所有的函数都有唯一的极值点，上面图中二次曲线有唯一的极值点属于简单情况.事实上很多函数是非常复杂的比如下图所示。同时初始点位置也很重要，如果我们起始点在下图右侧就滑入了局部最优解，如果在左侧就滑入了全局最优解，所以我们需要多次随机初始化我们的初始点，每次运行比较我们得到的最优解。因此梯度下降法的初始点的位置也是一个超参数。

image-20250921225807113

模拟实现梯度下降

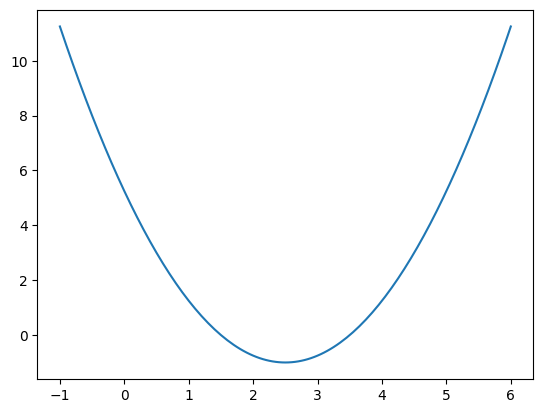
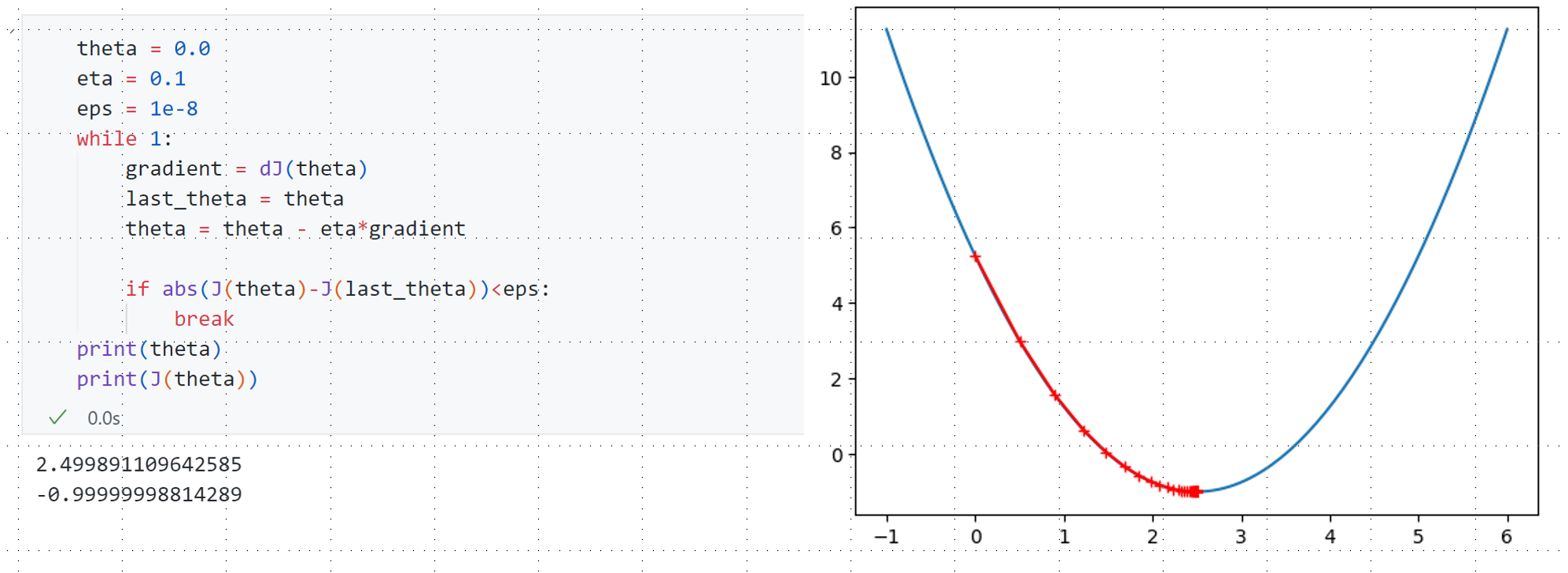
为了可视化方便依旧选用二次函数y=(x−2.5)2−1y=(x-2.5)^2-1 展示:

image-20250923160835368

​ 实现梯度下降法每一次都要计算损失函数对应的梯度，对上述函数求导dJ/dθ=2∗(θ−2.5)dJ/d\theta = 2*(\theta-2.5) ，同时还要确定θ\theta 这个值对应的损失函数是多少，这里损失函数是我们上面定义的J=(θ−2.5)2−1J=(\theta-2.5)^2-1 .

1
2
3
4
def dJ(theta):
    return 2*(theta-2.5)
def J(theta):
    return (theta-2.5)**2-1

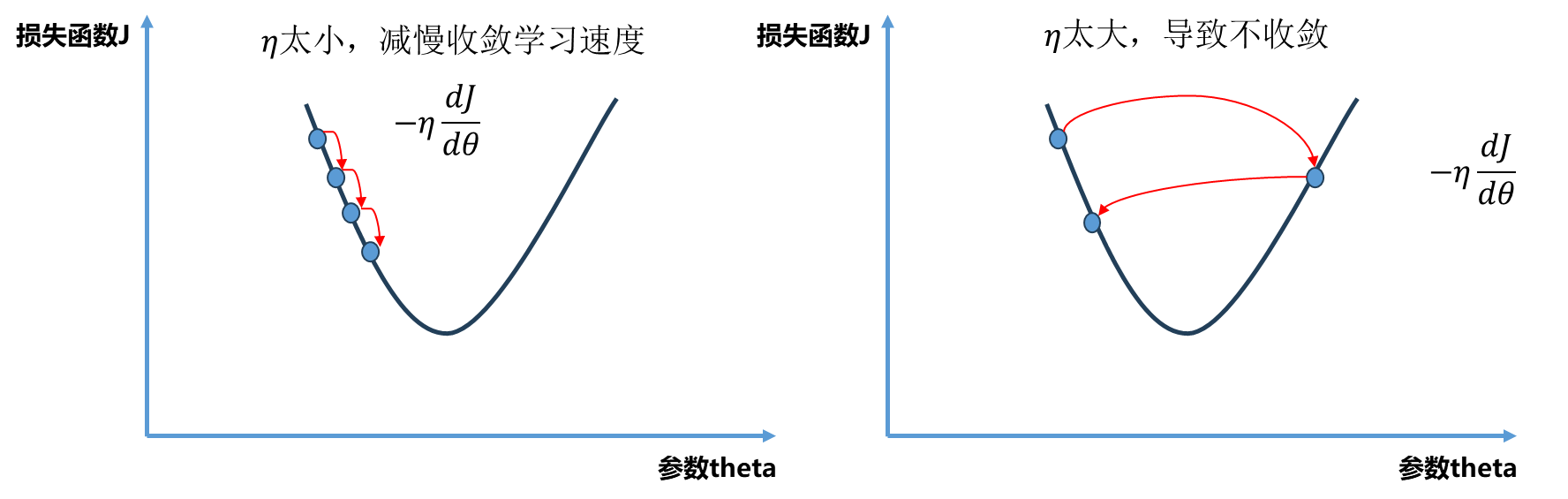
接下来开始梯度下降的过程：选取0为初始点，然后开始循环迭代，每一轮循环中首先求得当前点对应的梯度，接着θ\theta 向导数的负方向移动，同时这个移动有个步长η\eta 也就是学习率，最后我们要判断当前新的θ\theta 是否带我们来到函数的最小值的点，从理论上来说最小值点对应导数为0，但是编程具体实现时有可能因为η\eta 设置的不合适或者求导时的各种浮点精度问题使得最终求到的最小值θ\theta 的点达不到导数整整等于0的情况，而且计算机编程时对浮点数进行==的判断是危险的，主要是因为计算机计算浮点数是有误差的，很有可能永远达不到我们想要的精度。

既然如此，如何判断当前求得的θ\theta 达到最小值了呢？因为每次都是梯度下降，所以理论上每次求到一个新的θ\theta 之后，这个新的θ\theta 损失函数的值都应该比上一个θ\theta 对应的损失函数的值还要小，如果小的这部分 达到了精度要求比如下面设定为ϵ=1e−8\epsilon=1e-8 就可以退出循环。

具体实现如下：

image-20250923164245587

最终输出结果θ=2.4999,J(θ)=−0.9999\theta=2.4999,J(\theta)=-0.9999 从我们上面定义的J=(θ−2.5)2−1J=(\theta-2.5)^2-1 这个结果是正确的。右图可以发现θ\theta 从0点出发，刚开始梯度比较大，步长大，后面梯度平缓步长小，总共经过46次查找退出循环。

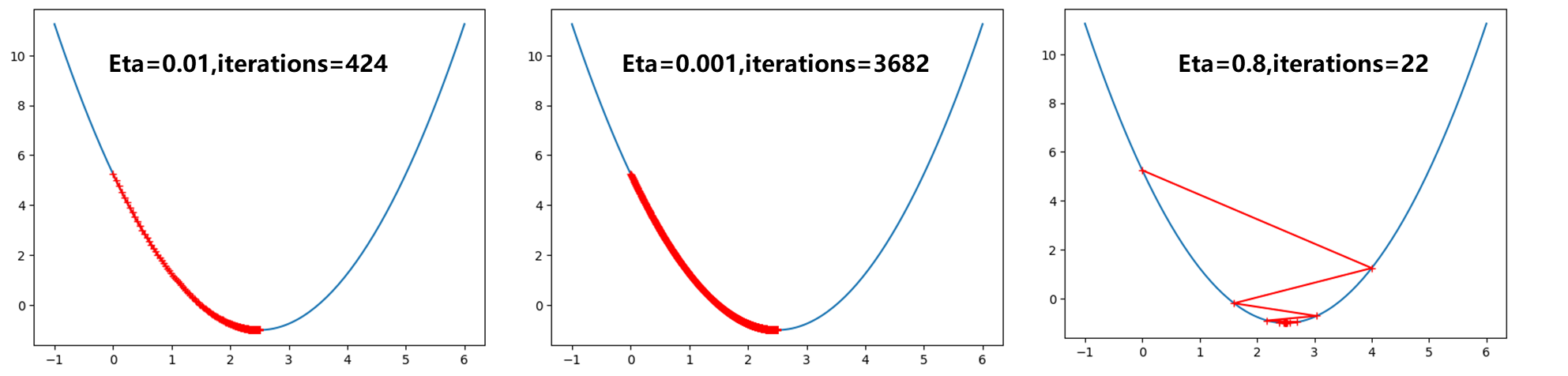
观察不同学习率时η\eta 的变化情况：

image-20250923165924900

η\eta 取0.01此时明显比取0.1路径更密，而0.001则是密集成了一条曲线了。而η\eta 取0.8可以发现曲线从开始0点跳到右半端，不过最后还是收敛到最小值点。

继续取大，当η\eta 取1.1时，出现了如下报错：OverflowError: (34, ‘Result too large’) .显然是因为此时1.1学习率过大，导致每次损失函数越跳越大，最后知道编译器报出警告。只绘制出前10次θ\theta 的变化情况:

image-20250923171114113

多元线性回归中的梯度下降

上面使用一个二次函数曲线模拟了梯度下降的过程，接下来将梯度下降应用到多元线性回归中。前面的博客讲到过多元线性回归的损失函数形式：

J=∑i=1m(y(i)−y^(i))2J=\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2

对于多元线性回归来说参数不止一个，n代表样本特征数量：

θ=(θ0,θ1,...,θn)\theta =(\theta_0,\theta_1,...,\theta_n)

所以我们要将上面二次函数例子中的dJ/dθdJ/d\theta 写成:

∇J=(∂J∂θ0,∂J∂θ1,...,∂J∂θn)\nabla J=(\frac{\partial J}{\partial\theta_0},\frac{\partial J}{\partial\theta_1},...,\frac{\partial J}{\partial\theta_n})

那么接下来详细推导一下线性回归法中的式子是什么样的：

note_1

采用上面最后的2/m2/m 的写法相当于我们的目标函数是下面这样的式子：

目标:使1m∑i=1m(y(i)−y^(i))2尽可能小J(θ)=MSE(y,y^)目标:使\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}-\hat{y}^{(i)})^2尽可能小\\ J(\theta)=MSE(y,\hat{y})

这个推导也说明一个道理：使用梯度下降法来求解一个函数最小值，有时候需要对目标函数进行一些特殊的设计，不见得所有的目标函数都非常的合适。

代码实现：

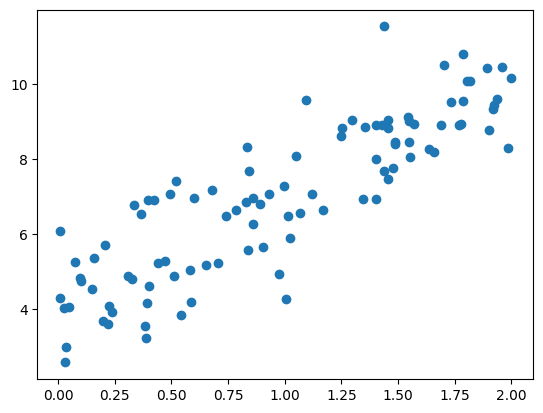
随机生成一组数据满足y=3x+4y=3x+4

1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
x = 2*np.random.random(size=100)
y = x*3. + 4. + np.random.normal(size=100)
X = x.reshape(-1,1)

plt.scatter(X, y)
plt.show()

可视化出来：

image-20250925175958099

接着同上面二次函数中的实现方法一样实现J,dJJ,dJ:

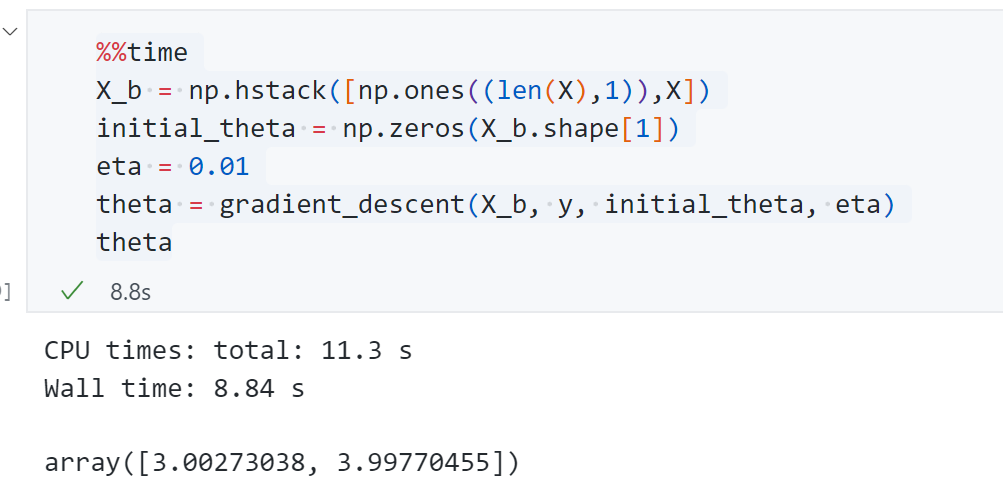
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
def J(theta, X_b, y):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(X_b)
    except:
        return float('inf')

def dJ(theta, X_b, y):
    res = np.empty(len(theta))
    res[0] = np.sum(X_b.dot(theta)-y)
    for i in range(1, len(theta)):
        res[i] = (X_b.dot(theta)-y).dot(X_b[:,i])
    return res * 2/len(X_b)
    
def gradient_descent(X_b, y , initial_theta, eta, n_iters=1e4, eps=1e-8):

    theta = initial_theta
    i_iter = 0
    while i_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta*gradient

        if abs(J(theta, X_b, y)-J(last_theta,X_b,y)) <eps:
            break
        i_iter +=1
    return theta

运行得到最终参数 分别为4.02145和3.007符合我们生成的 数据规律。

image-20250925180141629

封装方法到之前定义的LinearRegression类中：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40

def fit_gd(self, X_train, y_train, eta=0.01, n_iters=1e4):
    assert X_train.shape[0] == y_train.shape[0],\
    "the size of X_train must be equal to the size of y_train"

    def J(theta, X_b, y):
        try:
            return np.sum((y-X_b.dot(theta))**2)/len(X_b)
        except:
            return float('inf')
        
    def dJ(theta, X_b, y):
        res = np.empty(len(theta))
        res[0] = np.sum(X_b.dot(theta)-y)
        for i in range(1, len(theta)):
            res[i] = (X_b.dot(theta)-y).dot(X_b[:,i])
        return res * 2/len(X_b)   
        
    def gradient_descent(X_b, y , initial_theta, eta, n_iters=1e4, eps=1e-8):

        theta = initial_theta
        i_iter = 0
        while i_iter < n_iters:
            gradient = dJ(theta, X_b, y)
            last_theta = theta
            theta = theta - eta*gradient

            if abs(J(theta, X_b, y)-J(last_theta,X_b,y)) <eps:
                break
            i_iter +=1
        return theta

    X_b = np.hstack([np.ones((len(X_train),1)),X_train])
    initial_theta = np.zeros(X_b.shape[1])

    self._theta = gradient_descent(X_b, y_train , initial_theta, eta, n_iters=1e4)
    self.interception_ = self._theta[0]
    self.coef_ = self._theta[1:]

    return self

调用发现结果一致：

image-20250925181213219

向量化

接下来我们依旧尝试对梯度的形式进行向量化来为编程实现上提高效率。

68a1522927b87be2eda497d0ecc714ac

因此接下来可以将dJdJ 修改为下面的形式：

1
2
3
4
5
6
7
8
def dJ(theta, X_b, y):
    # 原来的做法：
    # res = np.empty(len(theta))
    # res[0] = np.sum(X_b.dot(theta)-y)
    # for i in range(1, len(theta)):
    #     res[i] = (X_b.dot(theta)-y).dot(X_b[:,i])
    # return res * 2/len(X_b)   
    return X_b.T.dot(X_b.dot(theta)-y)*2./len(y)

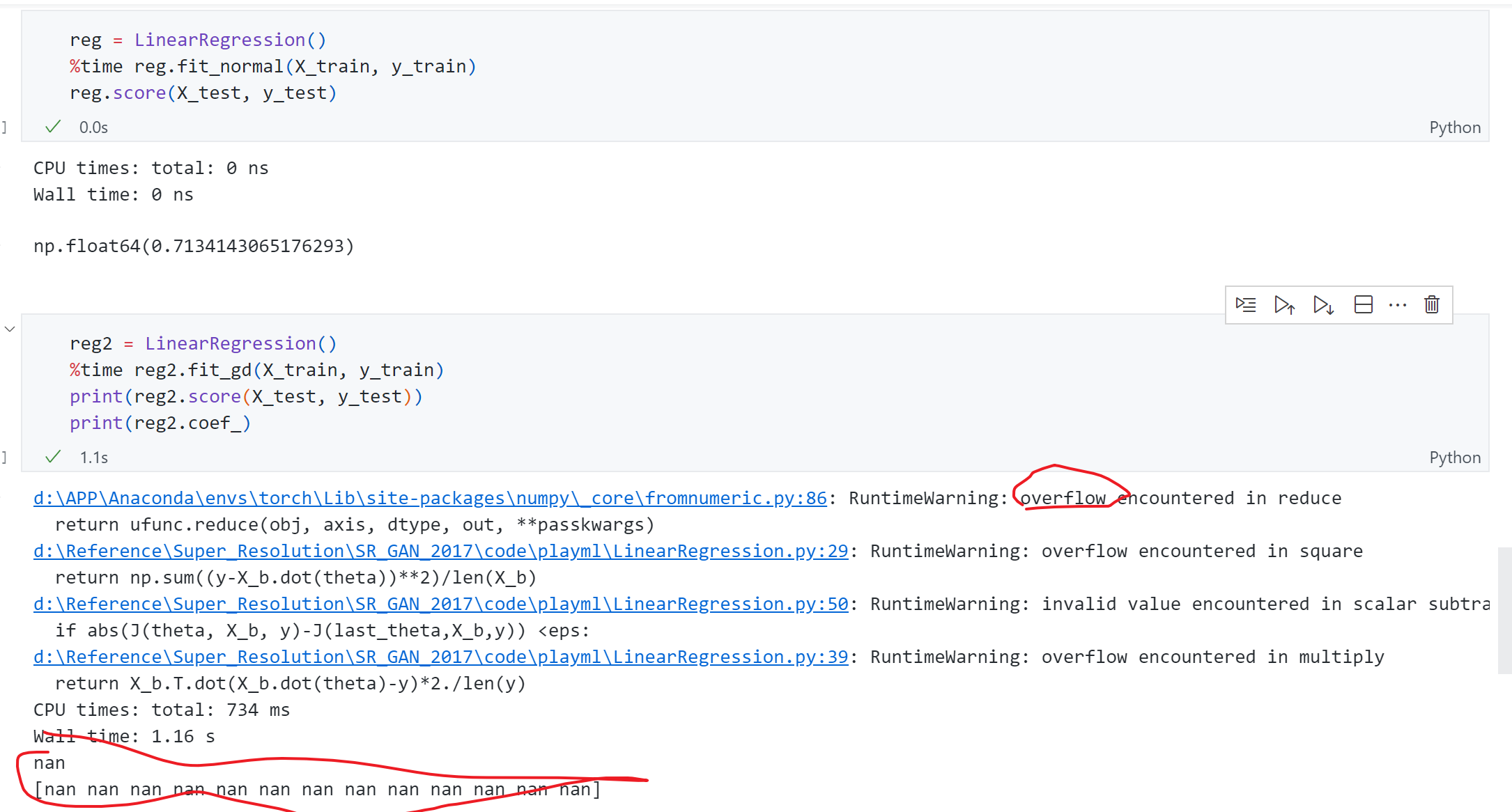
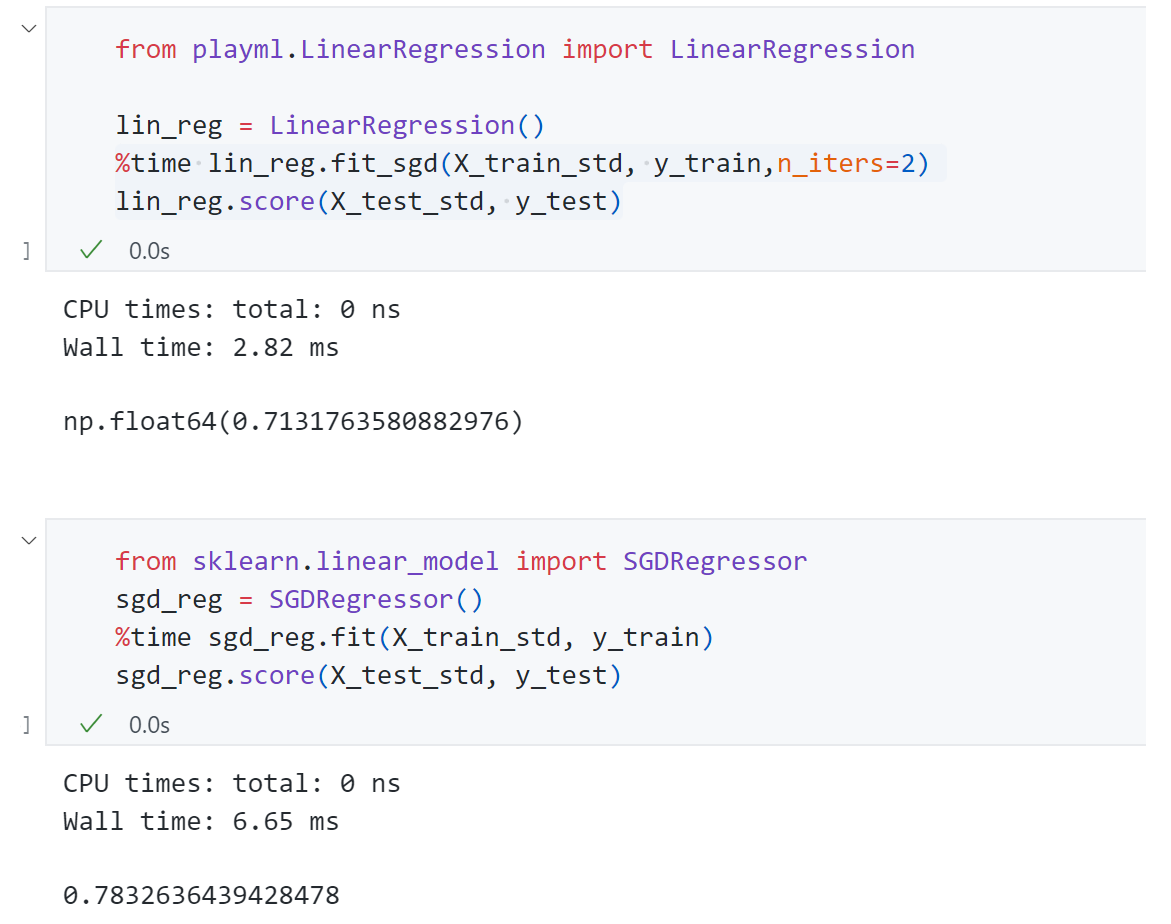
依旧针对Boston housing数据 进行测试，首先采用正规方程解的方式 得到score为0.71,而采用梯度下降时出现了overflow报错，同时结果全为nan,这是为什么？

主要原因是现在使用的Boston housing是一个真实数据集，观察一下可以发现每条数据的 各个维度上数据规模差异很大，有些特征是0.多，有些上百多，所以会导致 梯度下降时某些维度的梯度特别大即梯度爆炸。

image-20250926144804014

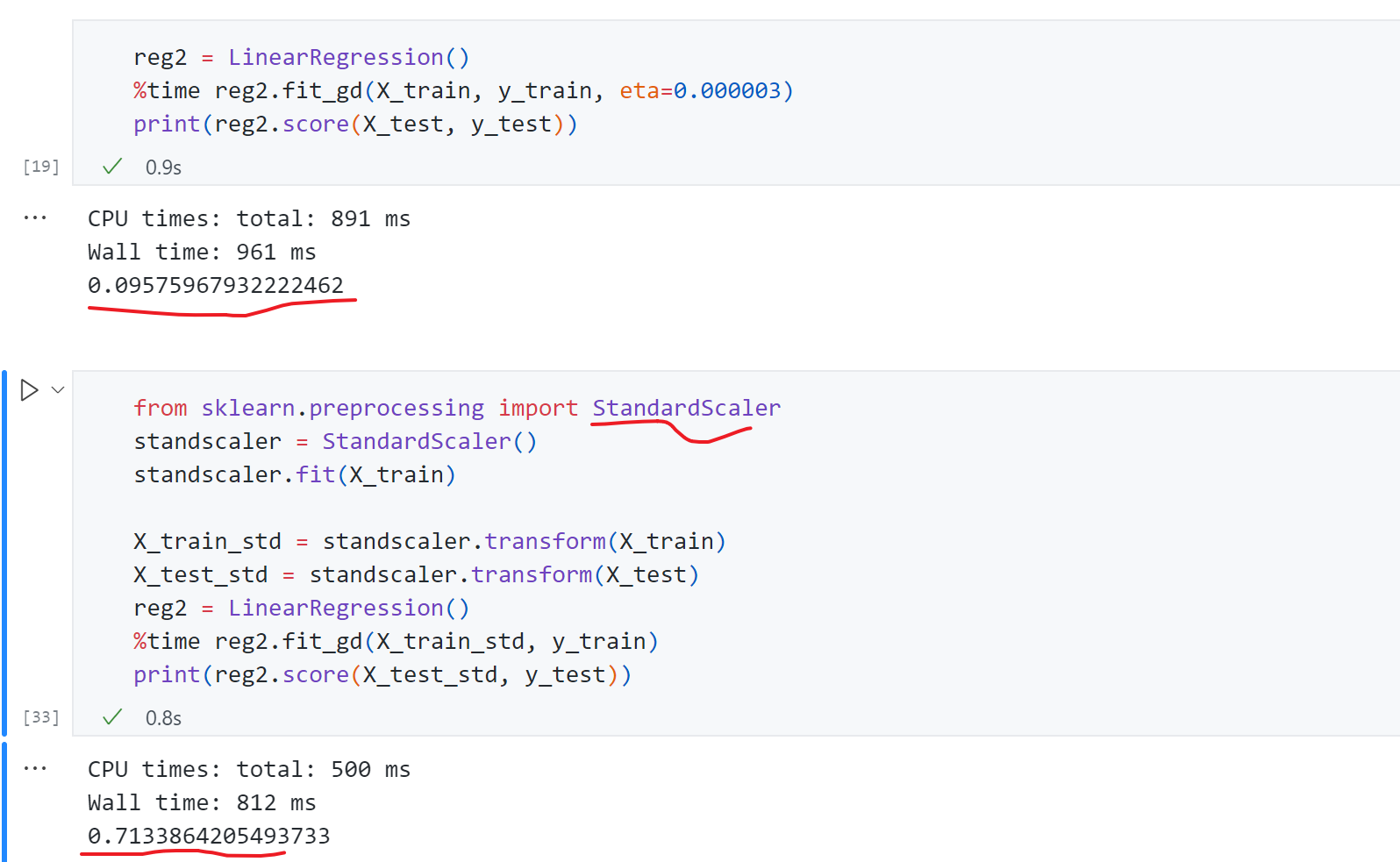
如何验证这一猜想呢？可以先尝试给学习率一个很小的值η=0.000003\eta=0.000003 ,此时没有报错score为0.09.显然此时的θ\theta 还不是我们想要的那个，损失函数还未到最小值。这背后的主要原因是数据不在一个规模上，因此我们需要数据归一化,通过数据归一化后我们再使用梯度下降法得到score为0.71，结果恢复了正常。

image-20250926150042795

梯度下降法速度优势

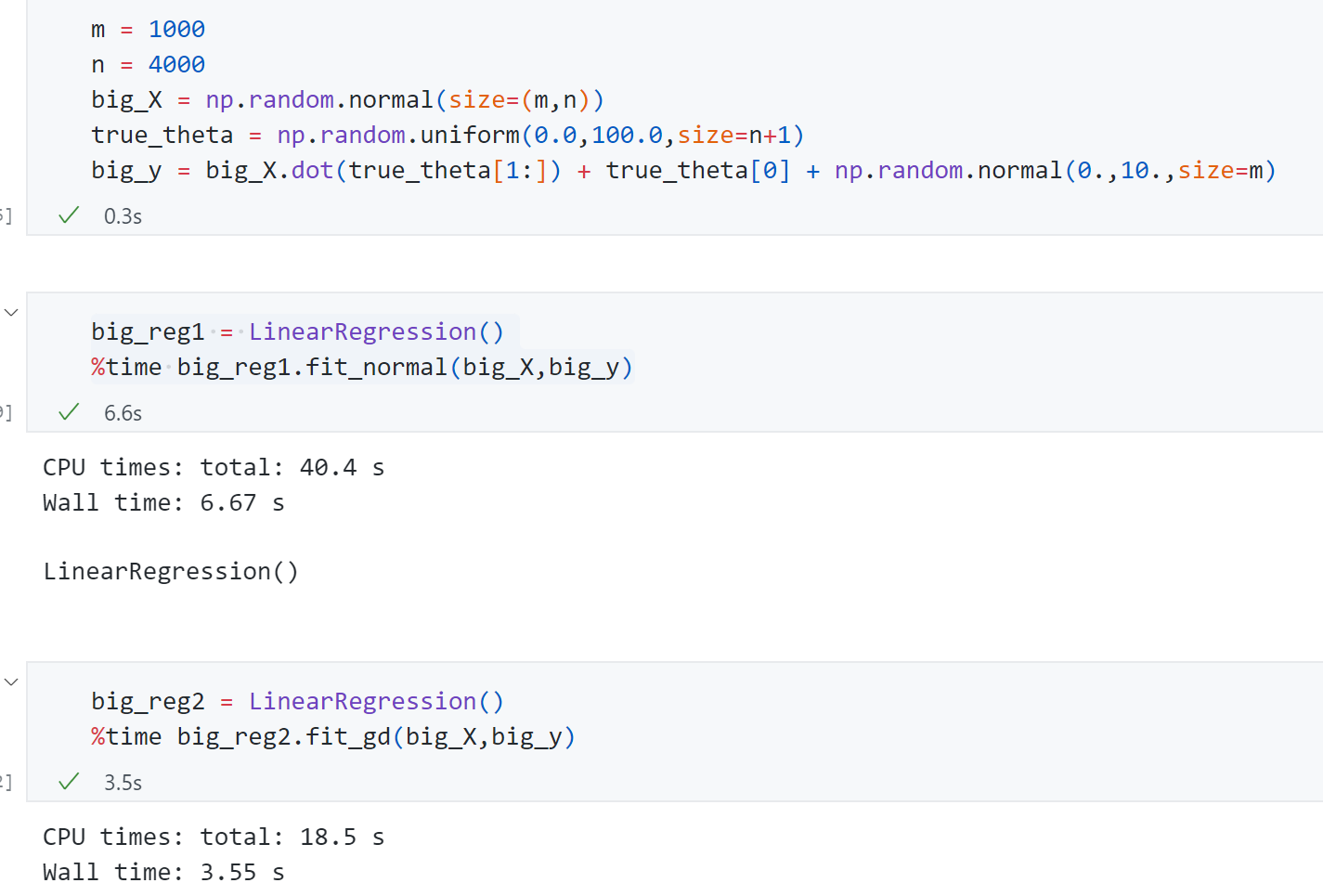
接下来生成随即生成一组样本数量1000，特征数量4000的样本。来比较使用正规方程和梯度下降的速度差异：

image-20250926151208430

可以发现梯度下降法只用了3.55s，而正规方程解用了6.67s.如果加大特征数梯度下降法的优势会更加明显。同时可以发现这组数据的样本数量是小于特征量的，我们现在采用的梯度下降法计算梯度时需要每一个样本都参与计算，这使得样本量比价大时我们相应计算梯度也比较慢，这也有一种改进的方式就是-----随机梯度下降法。

随机梯度下降法

前面推导多元线性回归时用到的梯度下降法每一项都要对所有的m即样本数进行计算，这种梯度下降法也叫做Batch Gradient Descent.这样显然也有一个问题就是如果样本数量m很大，那么计算梯度会非常耗时。‘

尝试将原来m个样本计算梯度变为计算一个样本：

image-20250926234446680

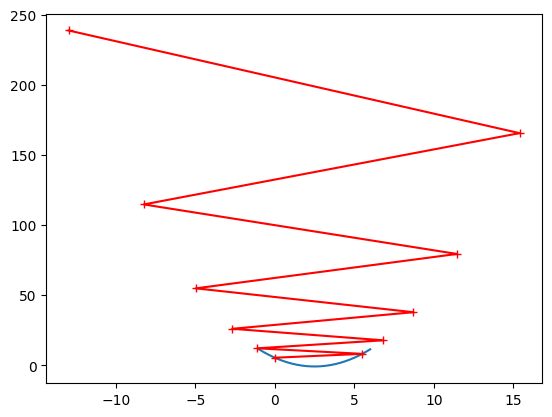
最终得到的式子可以作为我们搜索的方向，没说梯度的方向因为这个式子本身不是损失函数的梯度了。每次都随机取出一个样本i，然后计算这个式子得到一个方向不断搜索迭代，这样思想实现思路就是随机梯度下降法(Stochastic Gradient Descent).

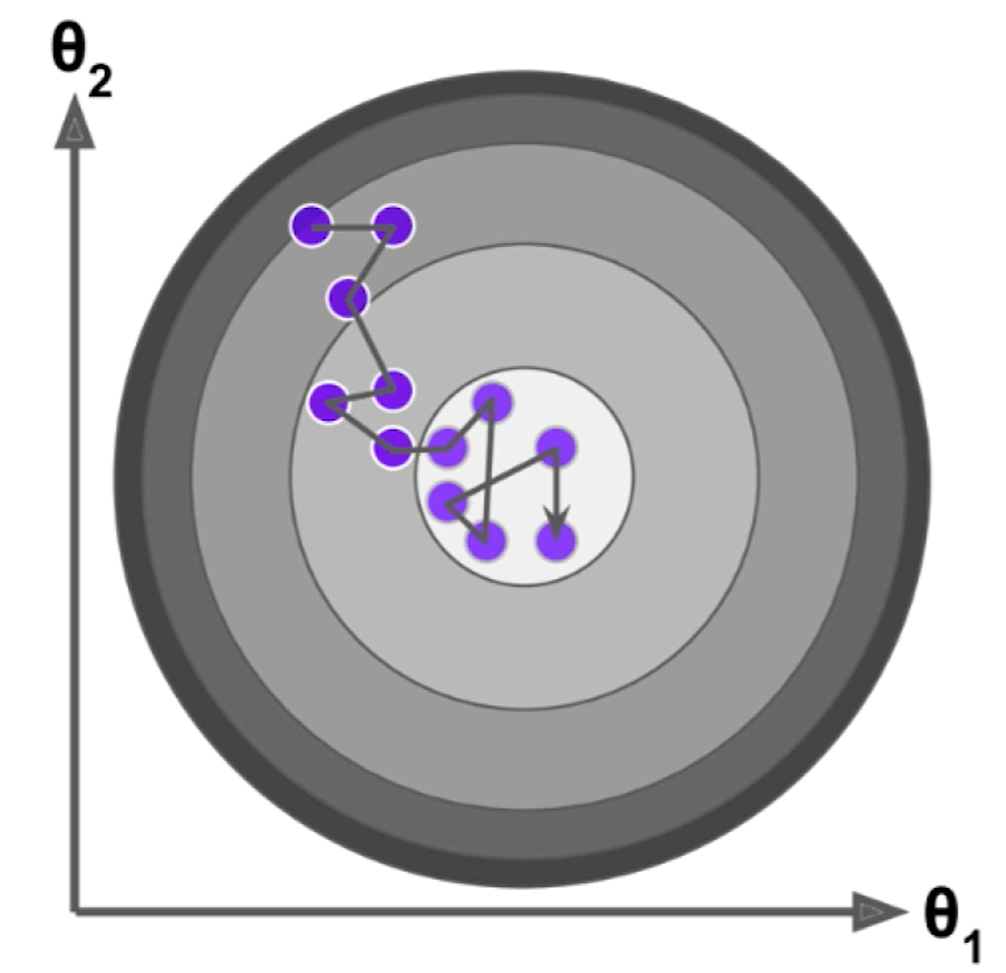
随机梯度下降的搜索过程可能如下面这个图所示，随机梯度下降不能保证每次得到的方向是损失函数减少的方向，更不能保证是减小方向最快的方向。

同时在具体实现的时候，在随机梯度下降法过程中学习率取值非常重要，因为随机梯度下降过程如果学习率一直取一个固定值的情况下，很有可能已经来到最小值中心左右位置时但是随机过程不够好同时η\eta 是一个固定值慢慢又跳出了这个最小值所在的位置，所以实际中希望随机梯度下降法中学习率是逐渐递减的。

那么可以设置一个函数使得学习率随着循环次数增加越来越小，一个简单的思路是采用 循环次数的倒数：

η=1n_iters\eta=\frac{1}{n\_{iters}}

但这个函数的一个问题是循环次数 比较小的时候η\eta值下降的太快了，所以通常实现会在分母上加个bb 来缓解这种情况,分子取a灵活一些。这也对应SGD的两个超参数，也这是模拟退火的思想。

η=an_iters+b\eta=\frac{a}{n\_iters+b}

编程实现：

  • 生成1百万个随机样本数据
1
2
3
4
5
6
7
8
9
import numpy as np
import matplotlib.pyplot as plt

m =1000000

x = np.random.normal(size=m)
X = x.reshape(-1,1)
X.shape
y = 4.*x + 3. + np.random.normal(0,3,size=m)
  • 先看一下 采用 Batch Gradient Descent 耗时：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
def J(theta, X_b, y):
    try:
        return np.sum((y-X_b.dot(theta))**2)/len(y)
    except:
        return float('inf')

def dJ(theta, X_b,y):
    return X_b.T.dot(X_b.dot(theta)-y)*2./len(y)

def gradient_descent(X_b, y ,initial_theta, eta,n_iters=1e4,eps=1e-8):

    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta,X_b,y)
        last_theta = theta
        theta = theta - eta*gradient

        if(abs(J(theta,X_b,y)-J(last_theta,X_b,y))<eps):
            break
        cur_iter+=1
    return theta
image-20250927005535178

耗时11.3s，预测的两个系数分别为3.00和3.99，与我们生成给的参数基本一致。

  • 采用随机梯度下降
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def dJ_sgd(theta, X_b_i,y_i):
    return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2

def sgd(X_b, y ,initial_theta,n_iters=1e4):

    t0=5
    t1=50

    def learning_rate(t):
        return t0/(t+t1)
    theta = initial_theta

    for cur_iter in range(n_iters):
        rand_i = np.random.randint(len(X_b))
        gradient = dJ_sgd(theta,X_b[rand_i],y[rand_i])
        theta = theta - learning_rate(cur_iter)*gradient
    return theta
image-20250927005646931

耗时1.8s,结果2.99和3.98与我们 生成的参数一致，但速度比Batch Gradient Descent快了5-6倍。

同理接下来对SGD方法进行封装：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def fit_sgd(self, X_train, y_train, n_iters=5, t0=5, t1=50):
    assert X_train.shape[0] == y_train.shape[0],\
    "the size of X_train must be equal to the size of y_train"     

    def dJ_sgd(theta, X_b_i,y_i):
        return X_b_i.T.dot(X_b_i.dot(theta)-y_i)*2

    def sgd(X_b, y ,initial_theta,n_iters=1e4,t0=5,t1=50):
        def learning_rate(t):
            return t0/(t+t1)
        theta = initial_theta
        m = len(X_b)
        for cur_iter in range(n_iters):
            indexes = np.random.permutation(m)
            X_b_new = X_b[indexes]
            y_new = y[indexes]

            for i in range(m):
                gradient = dJ_sgd(theta,X_b_new[i],y_new[i])
                theta = theta - learning_rate(cur_iter*m+i)*gradient
        return theta  

    X_b = np.hstack([np.ones((len(X_train),1)),X_train])
    initial_theta = np.zeros(X_b.shape[1])

    self._theta = sgd(X_b, y_train , initial_theta,n_iters,t0,t1)
    self.interception_ = self._theta[0]
    self.coef_ = self._theta[1:]

    return self

依旧应用到 Boston Housing数据上：

image-20250927013352198

可以发现scikit-learn的效果比我们实现的效果要好。

梯度的调试（*）

使用梯度下降法很重要的一个点是求出损失函数在对应θ\theta 点的梯度是什么。前面也是花了很多时间推导求梯度的公式，接着向量化等等。然而对于一些复杂的函数求解梯度可能并不容易，并且推导出公式后程序运行实现可能程序不会报错，但是梯度却求的是错误的。这种情况下如何发现这种错误呢？

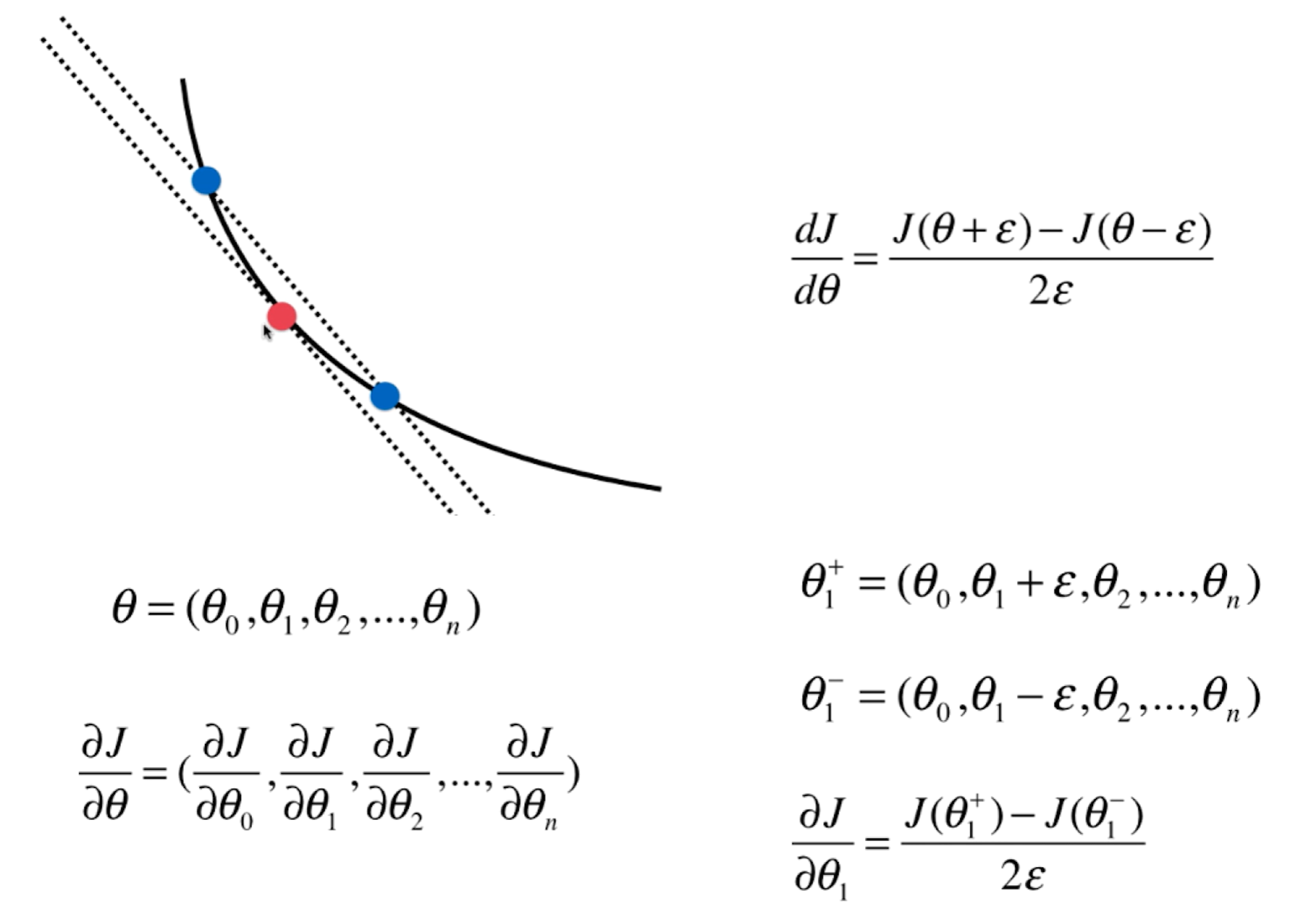
对于一个点的梯度我们可以导数定义出发，通过在红点左右分别取一蓝点，当这个间距越小，此时这个斜率越接近红点的导数。同样对于多维度对每个维度用这种方式求解即可。

image-20250927022840251

代码实现：

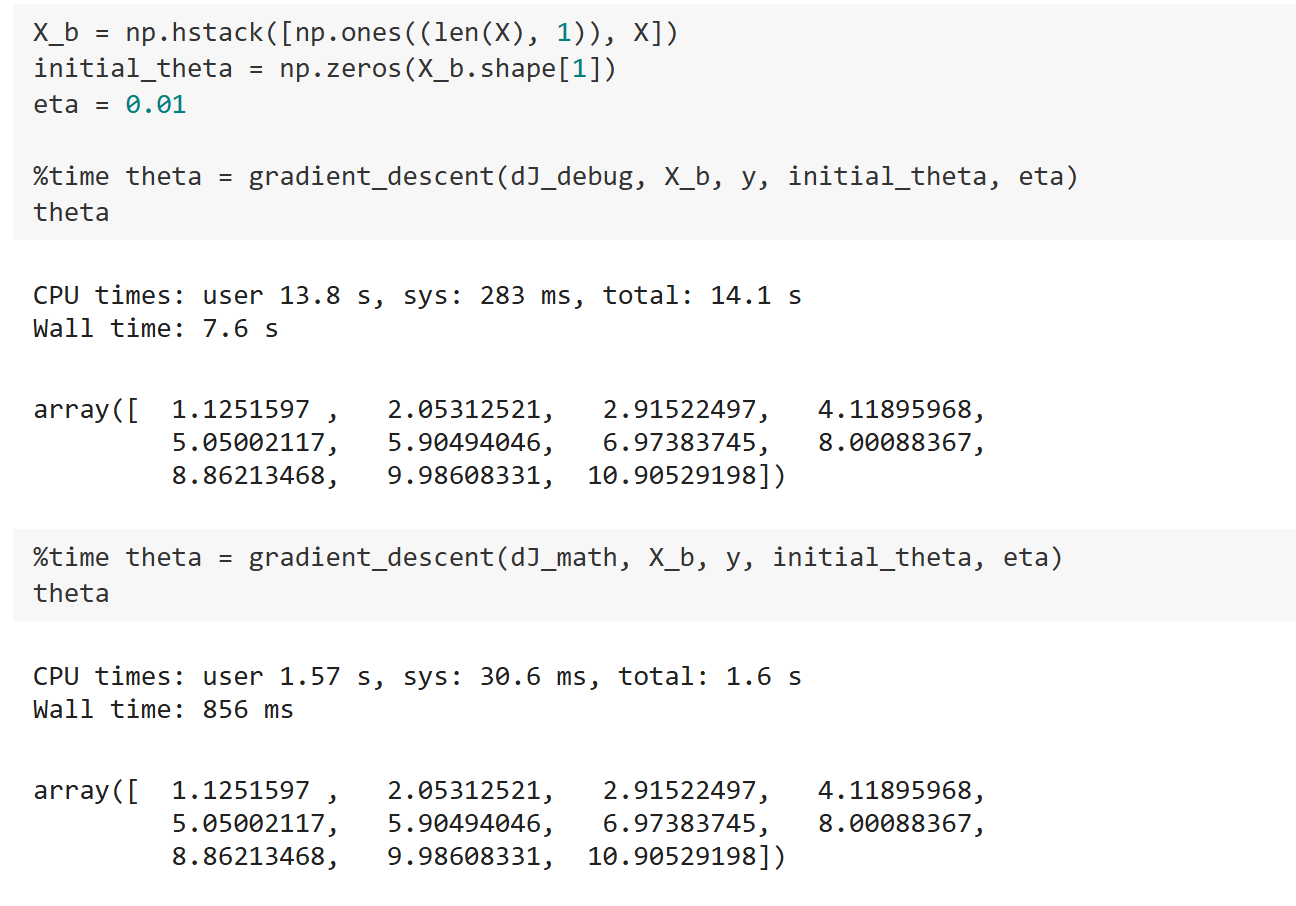
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
import numpy as np
import matplotlib.pyplot as plt
np.random.seed(666)
X = np.random.random(size=(1000, 10))

true_theta = np.arange(1, 12, dtype=float)
X_b = np.hstack([np.ones((len(X), 1)), X])
y = X_b.dot(true_theta) + np.random.normal(size=1000)

def J(theta, X_b, y):
    try:
        return np.sum((y - X_b.dot(theta))**2) / len(X_b)
    except:
        return float('inf')
def dJ_math(theta, X_b, y):
    return X_b.T.dot(X_b.dot(theta) - y) * 2. / len(y)
def dJ_debug(theta, X_b, y, epsilon=0.01):
    res = np.empty(len(theta))
    for i in range(len(theta)):
        theta_1 = theta.copy()
        theta_1[i] += epsilon
        theta_2 = theta.copy()
        theta_2[i] -= epsilon
        res[i] = (J(theta_1, X_b, y) - J(theta_2, X_b, y)) / (2 * epsilon)
    return res
def gradient_descent(dJ, X_b, y, initial_theta, eta, n_iters = 1e4, epsilon=1e-8):
    
    theta = initial_theta
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = dJ(theta, X_b, y)
        last_theta = theta
        theta = theta - eta * gradient
        if(abs(J(theta, X_b, y) - J(last_theta, X_b, y)) < epsilon):
            break
            
        cur_iter += 1

    return theta

观察结果：

image-20250927023139689

可以发现使用dJdebugdJ_{debug} 这种方式最终可以求解梯度的，结果与通过数学公式推导的结果近似，但是训练速度会慢很多。因此如果机器学习算法涉及梯度的求法时候，完全可以采用dJdebugdJ_{debug} 这种求法得到一个正确结果，然后再去推导梯度数学解代入得到结果，看这个结果是否与dJdebugdJ_{debug} 的结果一样来验证推导结果是否正确。这是一个很有用的技巧，并且dJdebugdJ_{debug} 这种方式可以复用，而dJmathdJ_{math} 则依赖于当前损失函数的推导，所以dJdebugdJ_{debug} 求梯度的方法非常实用。

一些思考总结

前面主要说了两种梯度下降法：

  • 批量梯度下降法 Batch Gradient Descent:对所有的样本求解，速度慢，但是稳定，一定可以向损失函数下降最快方向前进。
  • 随机梯度下降法 Stochastic Gradient Descent:每次只对一个样本求解，快，但是不稳定，甚至可能反方向前进。

综合这两种梯度下降法就有了小批量梯度下降法Mini-Batch Gradient Descent,每次看k个样本，兼顾两种方法。

同时梯度下降法不是一个机器学习算法，是一种基于搜索的最优化方法，可以最小化一个损失函数或者梯度上升法最大化一个效用函数。