机器学习(6):PCA2025.10.051 Categories / 1 Tags
Blog Post

机器学习(6):PCA

2025.10.05机器学习机器学习
机器学习(6):PCA

PCA

上一篇详细介绍了梯度下降法，梯度下降法主要是寻找目标函数最优解的一种方式。这次介绍一下另外一个梯度寻找的应用—Principal Component Analysis(PCA). PCA是很有名的一种算法，不仅应用在机器学习领域，也是统计学领域非常重要的一种方法。它本身是一个非监督学习的算法，主要用于数据的降维，通过降维可以提高算法的效率，可以发现更多便于人类理解的特征，同时也方便可视化以及去噪，通过PCA去噪在应用机器学习算法效果可能更好。

什么是主成分分析？

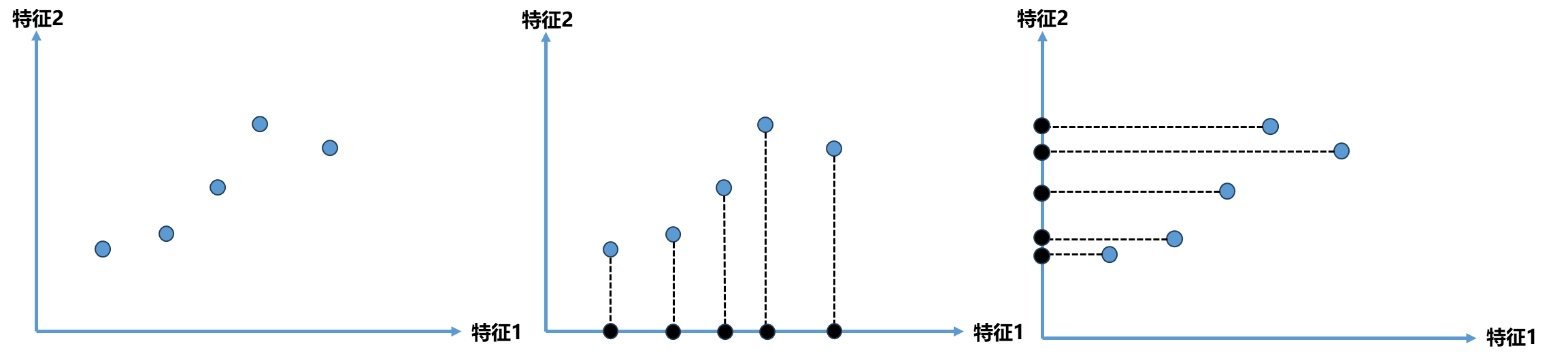
主成分分析的主要作用是降维，基于这一点可以先来理解一下其的原理。下面图中是一个二维平面，横轴和纵轴代表样本点的两个特征。既然这都是二维特征的样本，如果降维那么如何降到1维呢？一个直观的思路是将这两个特征中的一个特征丢掉，比如图(中)是将特征2丢掉，图(右)是将特征1丢掉。

image-20250928162547262

这两种方案哪个更好呢？显然图(中)的方案会让人觉得更好，这个方案是将所有点映射到x轴上，映射完后点和点之间的距离相对较大，即点与点之间有相应的更高的区分度，同时距离相对较大也保持了原来点和点之间的距离。而图(右)的方案将所有点映射到y轴后，点与点之间的距离相对更密了，这和原来点和点之间的分布相对而言差异更大了。因此如果要选择一种方案的话我们应该会更倾向选择中间的方案。

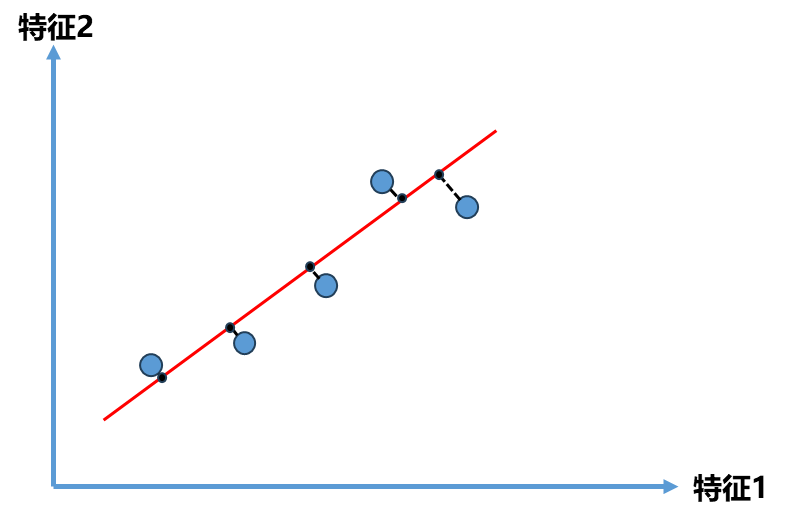
但是也不得不思考这种方案是最好的方案吗？我们原来的目的是想将图左中的点由二维平面降到一维平面，那么应该也会有一条直线如下图中斜着的红线，如果将所有点映射到这条直线上，它们整体分布和原来的样本并没有很大的差距，同时所有的点都在一个轴上。即使这个轴是斜的，我们也可以理解成一个轴一个维度，通过这样的方式我们将点从2维降成了1维，同时这种方式所有点更加趋近原来点的分布情况，也比前面映射到x轴或y轴间距都更加的大，区分度也更加明显。

image-20250928174820136

由此问题转为了如何找到这个让样本间距最大的轴？那么第一个问题就是如何定义样本间距？统计学中可以直接用方差(Variance)来定义样本间距：
$$
Var(x)=\frac{1}{m}\sum_{i=1}^{m}(x_i-\bar{x})^2
$$
那么进一步我们的目标就是找到一个轴，使得样本空间所有的点映射到这个轴后，方差最大。

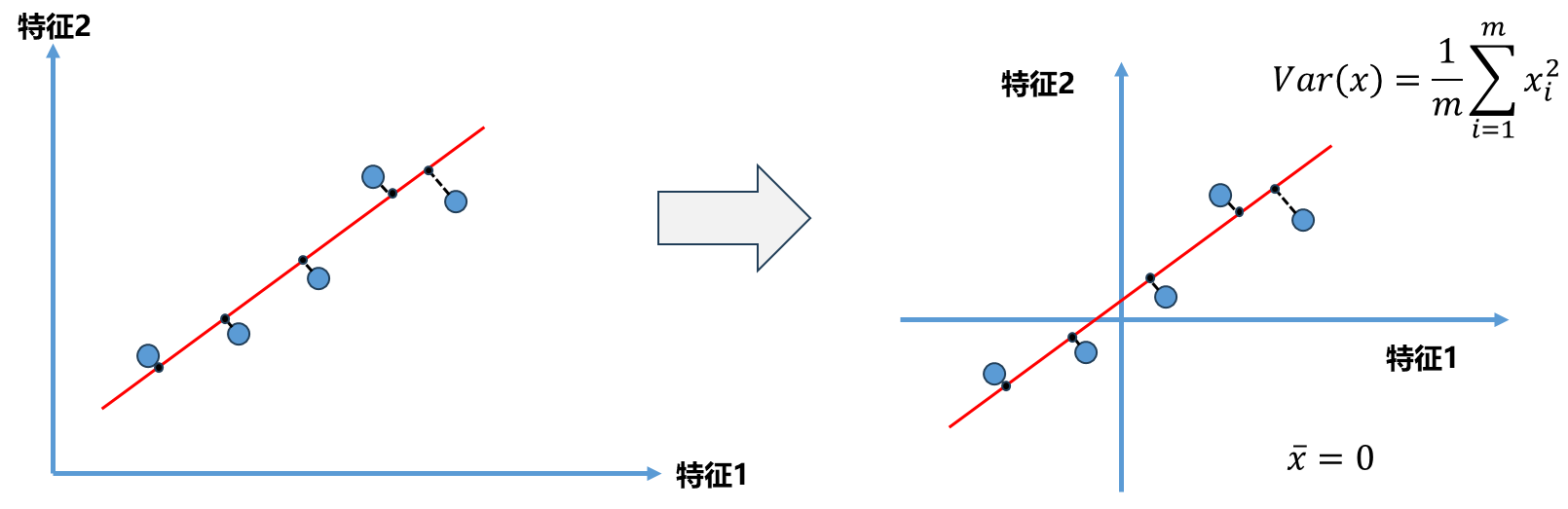
  • Step1:为了解决这个问题，在进行主成分分析之前，首先要对所有的样本均值归0(demean).

image-20250928180823191

样本分布没有改变，只是对坐标轴进行了移动，使得样本在每一个维度均值都为0.同时我们的方差公式得到了化简。

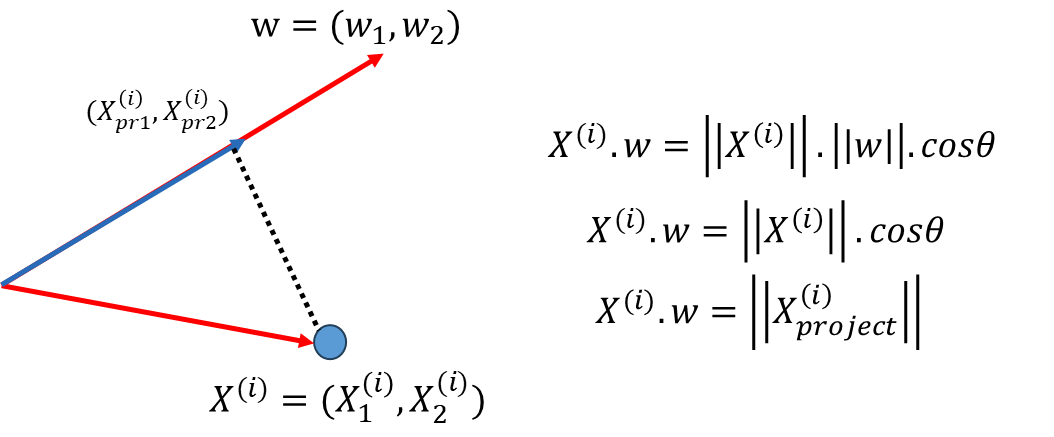
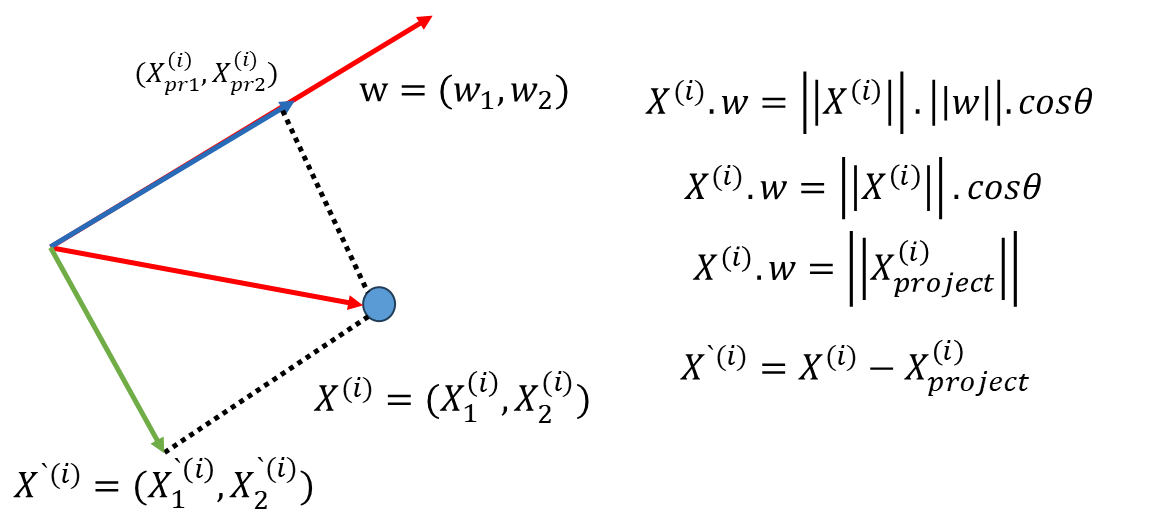
  • 接下来我们就是相求一个轴的方向（这里取2维演示）$w=(w_1,w_2)$ ，使得所有的样本映射到$w$ 以后有：

$$
Var(X_{project})=\frac{1}{m}\sum_{i=1}^{m}||X_{project}^{i}-\bar{X}_{project}||^2
$$

由因为前面demean后的$\bar{X}{project}=0$，可以得到：
$$
Var(X{project}）=\frac{1}{m}\sum_{i=1}^{m}||X_{project}^{(i)}||^2
$$
那么如何使上面这个式子最大呢？假设下图中红色的线是我们要找的方向$w=(w_1,w_2)$ ,每一个蓝色样本点$X^{(i)}$ 此时也是一个向量，将$X^{(i)}$ 映射到$w$ 上如图中的蓝线。此时求$||X_{project}^{(i)}||^2$ 相当于求蓝色直线长度的平方，这种映射刚好就是点乘的定义，$w$ 我们用方向向量表示则$||w||=1$ ，因此最终得到$X^{(i)}.w=||X_{project}^{(i)}||$

image-20250929020114178

进一步将上面式子带入可得：
$$
Var(X_{project}）=\frac{1}{m}\sum_{i=1}^{m}||X^{(i)}.w||^2
$$
因此到这一步PCA的目标为：
$$
目标：求w,使得Var(X_{project}）=\frac{1}{m}\sum_{i=1}^{m}||X^{(i)}.w||^2最大\
$$
如果$w，X^{(i)}$为n维的话，进一步可以展开：
$$
Var(X_{project}）=\frac{1}{m}\sum_{i=1}^{m}(X^{(i)}{1}.w_1+X^{(i)}{2}.w_2+…+X^{(i)}{n}.w_n)^2\
Var(X{project}）=\frac{1}{m}\sum_{i=1}^{m}(\sum_{j=1}^{n}X^{(i)}_{j}.w_j)^2
$$
显然此时PCA成了一个目标函数的最优化问题，可以使用梯度上升法解决。

梯度上升法求解PCA问题

$$
目标:求w,使得f(X)=\frac{1}{m}\sum_{i=1}^{m}(X_1^{(i)}w_1+X_2^{(i)}w_2+…+X_n^{(i)}w_n)^2最大\
\triangledown f=\begin{pmatrix}
\frac{\partial f}{\partial w_1} \
\frac{\partial f}{\partial w_2} \
…\
\frac{\partial f}{\partial w_n}
\end{pmatrix}
= \frac{2}{m}
\begin{pmatrix}
\sum_{i=1}^{m}(X^{(i)}{1}.w_1+X^{(i)}{2}.w_2+…+X^{(i)}{n}.w_n).X^{(i)}{1} \
\sum_{i=1}^{m}(X^{(i)}{1}.w_1+X^{(i)}{2}.w_2+…+X^{(i)}{n}.w_n).X^{(i)}{2} \
…\
\sum_{i=1}^{m}(X^{(i)}{1}.w_1+X^{(i)}{2}.w_2+…+X^{(i)}{n}.w_n).X^{(i)}{n}
\end {pmatrix}\
= \frac{2}{m}
\begin{pmatrix}
\sum_{i=1}^{m}(X^{(i)}.w).X^{(i)}{1} \
\sum{i=1}^{m}(X^{(i)}.w).X^{(i)}{2} \
…\
\sum{i=1}^{m}(X^{(i)}.w).X^{(i)}{n}
\end {pmatrix}\
=\frac{2}{m}.(X^{(1)}w,X^{(2)}w,..X^{(m)}w).\begin{pmatrix}
X^{(1)}{1} &X^{(1)}{2}&…&X^{(1)}{n}\
X^{(2)}{1} &X^{(2)}{2}&…&X^{(2)}{n}\
…\
X^{(m)}{1}&X^{(m)}{2}&…&X^{(m)}{n}
\end {pmatrix}\
=\frac{2}{m}.(Xw)^TX
$$

此时得到的向量形状为$1\times n$ 在经过一个转置:
$$
\triangledown f=\frac{2}{m}.X^T(Xw)
$$

求数据的主成分PCA

接下来开始编程实际看一下PCA的具体应用：

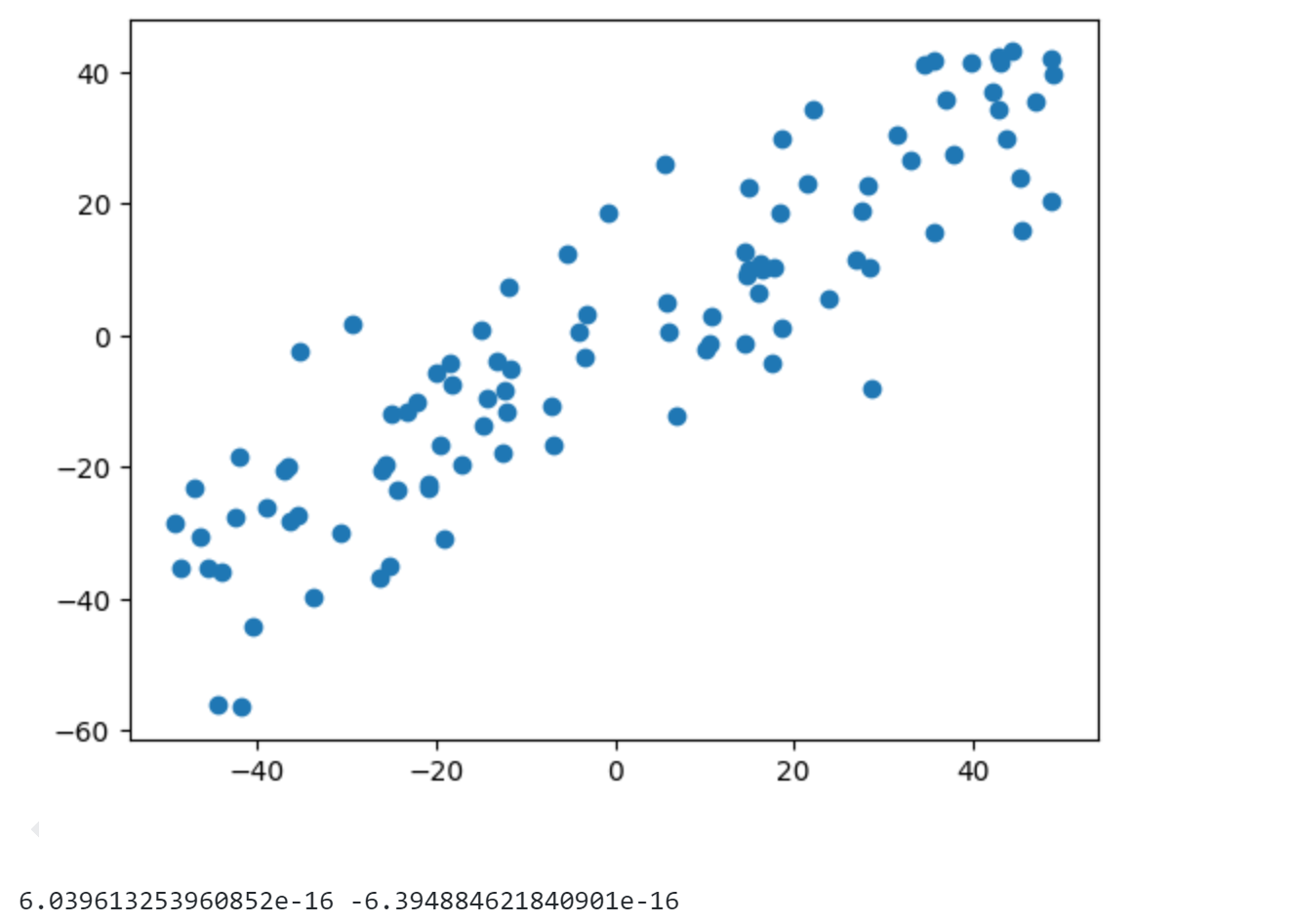
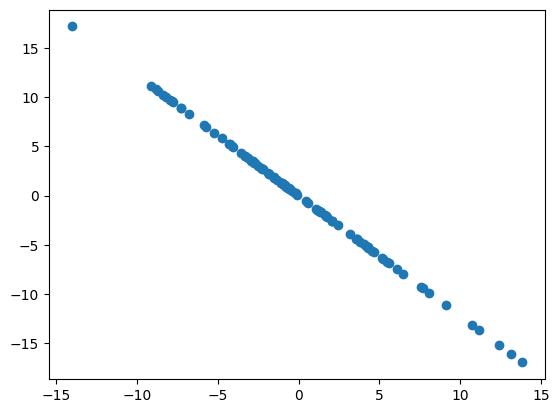
  • 首先生成100个假数据，数据包含两个特征，并且特征2和特征1还保持了一定的线性关系(这样降维效果比较明显)
1
2
3
4
5
6
import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100,2))
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. + np.random.normal(0, 10., size=100)
  • 对数据进行demean操作
1
2
3
4
5
6
7
8
def demean(X):
	return X - np.mean(X, axis=0)

X = demean(X)
plt.scatter(X[:,0],X[:,1])
plt.show()

print(np.mean(X[:,0]).item(),np.mean(X[:,1]).item())
image-20250929154434968

可以发现经过demean后数据的两个特征打印出来的均值6.03e-16和-6.39e-16基本为0.

  • 梯度上升法求取主成分
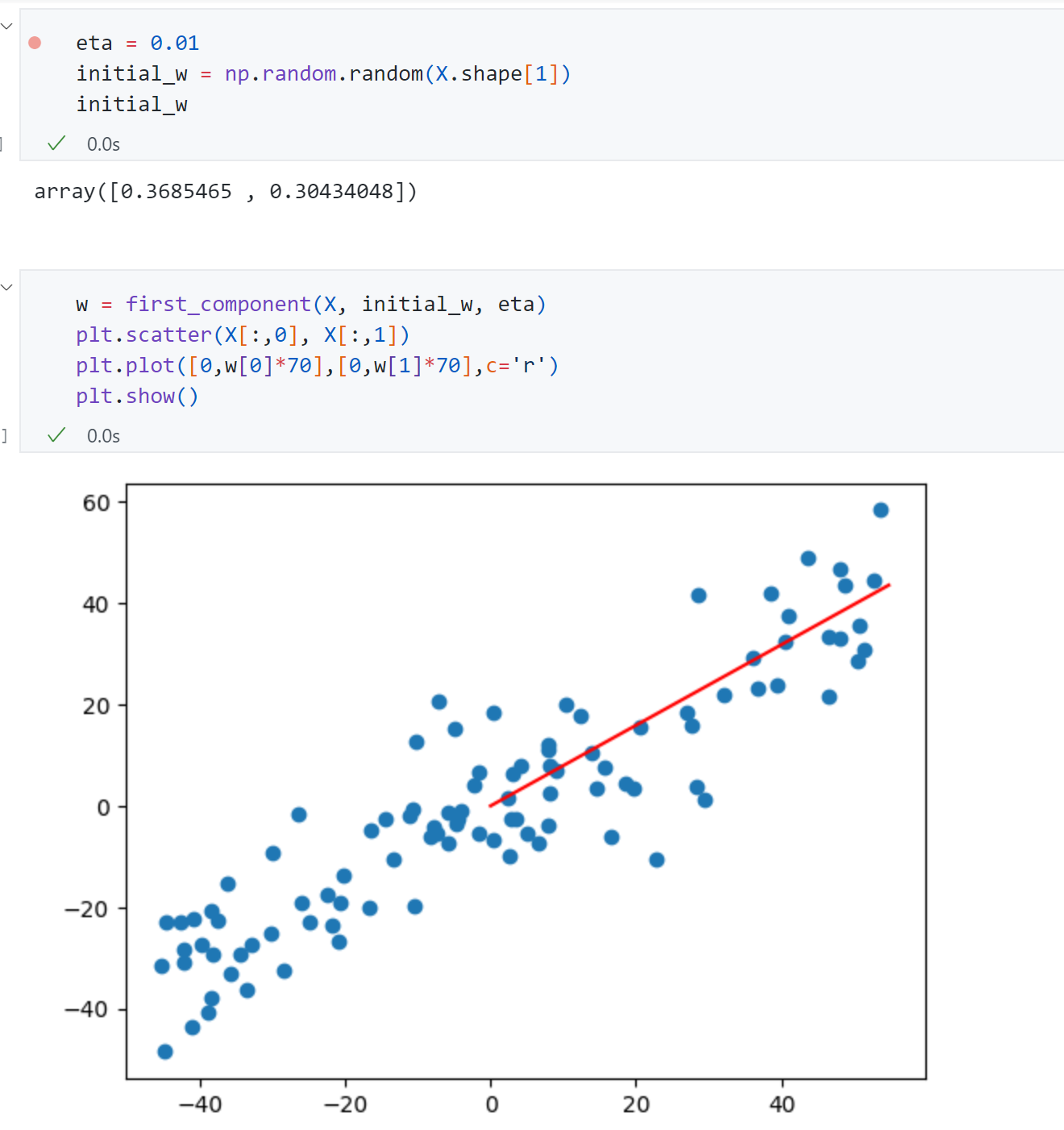
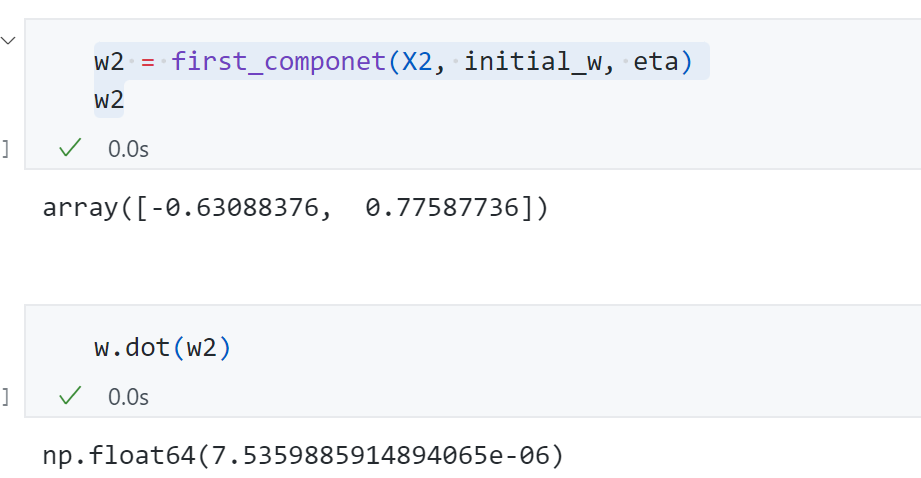
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def f(w, X):
    return np.sum(X.dot(w)**2)/len(X)

def df(w, X):
    return X.T.dot(X.dot(w))*2./len(X)

def direction(w):
    return w / np.linalg.norm(w)  # 求w的模 转化为单位向量

def first_component(X, initial_w, eta, n_iters = 1e4, epsilon=1e-8):
    
    w = direction(initial_w)
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta*gradient # 梯度上升 而非梯度下降
        w = direction(w)  # 转换为单位 方向向量

        if abs(f(w, X)-f(last_w, X)) < epsilon:
            break
    cur_iter +=1
    
    return w

上面的代码实现跟上篇的梯度下降法流程基本相同，唯一不同的是这里是求目标函数最大值采用的梯度上升 。这里的$w$ 本身也代表着一个方向向量，如果不变成单位向量的话它的模可能远远大于1导致搜索的过程不顺，为了得到合理的结果我们可能会将$\eta$ 的值变小，相应的循环次数也会增多，搜索性能也会下降。因此这里定义了一个求解方向向量的函数$direction$ ,因为前面的公式推导中我们假设了这个方向向量为单位向量模为1，从而简化了推导同时便于结果的搜索。

  • 初始化$w,\eta$ 进行求解：
image-20250929162315264

前面多元线性回归中$\theta$ 初始成了零向量，但PCA这里的$initial_w$ 不能选为零向量， 因为根据前面的推导可知我们的目标函数$f$以及梯度$df$ 的表达式如果$w$ 取0，则梯度为0，同时此时$w=0$ 本身就是一个极值点，但是一个极小值点，会导致后续无法更新。其次前面线性回归前要对样本数据进行标准化归一化的处理，但对于PCA这里不能进行标准化这个过程，因为PCA内部实现是要基于给定的数据X，由于对数据进行归一化对于数据X本身来说不是一个线性变化，因此如果对数据进行了标准化归一化，最终求得主成分坐标轴方向将和原始数据方向不一样的。

最后上面求得主成分方向$[0.37,0.30]$ 并以红线的形式绘制到了图中，可以发现该第一主成分非常贴合我们前面的思路。

求数据的前n主成分

上面使用梯度上升法求出了对于这组数据来说的第一个主成分，它是一个坐标轴对应的方向。同时前面所用的数据都是二维坐标点，将其映射到第一个主成分的轴后，它还不是一个一维的数据，只是将原来两个轴其中的一个轴变成了红色的轴，相应的它还是一个二维的数据，它还有第二个轴。同理对于n维数据来说它还是有n个轴，不过现在这n个轴通过主成分分析的方法从新进行了排列，使得第一个轴保持这些样本的方差相应是最大的，第二个轴次之，第三个轴在次之，以此类推。

换句话说，PCA本质上是从一组坐标系转移到另外一个坐标的过程。

那么求出第一主成分后，如何求出下一个主成分？

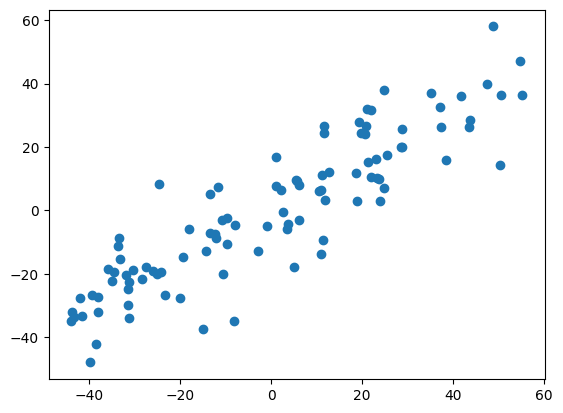
既然已经求出第一主成分了，可以对数据进行改变，将数据在第一个主成分上的分量去掉(如下图中绿色的线)。这样求得一组新的数据样本$X^{`}$ .

image-20250930144954547

接下来求第二主成分就相当于在新的数据$X^{`}$ 上求第一主成分，这个过程以此类推就可以求出第三主成分、第四主成分。

编程实现：

  • 随机生成一组样本
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
import matplotlib.pyplot as plt

X = np.empty((100,2))
X[:, 0] = np.random.uniform(0.,100.,size=100)
X[:, 1] = 0.75 * X[:,0] + 3. + np.random.normal(0,10.,size=100)

def demean(X):
    return X - np.mean(X, axis=0)
X =demean(X)

plt.scatter(X[:,0], X[:,1])
plt.show()

image-20250930163733387

  • 求解第一主成分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
def f(w, X):
    return np.sum(X.dot(w)**2)/len(X)

def df(w, X):
    return X.T.dot(X.dot(w))*2./len(X)

def direction(w):
    return w / np.linalg.norm(w)

def first_componet(X, initial_w, eta, n_iters=1e4, eps=1e-8):

    w = direction(initial_w)
    cur_iter = 0

    while cur_iter < n_iters:
        gradient = df(w, X)
        last_w = w
        w = w + eta*gradient
        w = direction(w)

        if abs(f(w,X)-f(last_w, X)) <eps:
            break
        cur_iter +=1
    
    return w
    
initial_w = np.random.random(X.shape[1])
eta = 0.01
w = first_componet(X, initial_w, eta)
w

得到第一主成分$w$结果为$[0.774,0.633]$.

  • 去除第一主成分的分量
1
2
3
4
5
X2 = np.empty(X.shape)
X2 = X - X.dot(w).reshape(-1,1)*w

plt.scatter(X2[:,0],X2[:,1])
plt.show()

image-20250930163910476

  • 在新的数据上求解第一主成分即 原来数据的第二主成分
image-20250930165042577

第二主成分结果为$[-0.63,0.77]$ ，与第一主成分进行点乘结果 基本为0也验证了第二主成分与第一主成分基本垂直。

  • 封装成求第n个主成分
1
2
3
4
5
6
7
8
9
10
11
12
13
14
def first_n_componet(n, X, eta=0.01, n_iters=1e4, eps=1e-8):

    X_pca = X.copy()
    X_pca = demean(X_pca)
    res = []

    for i in range(n):
        initial_w = np.random.random(X_pca.shape[1])
        w = first_componet(X_pca, initial_w, eta)
        res.append(w)
        
        X_pca = X_pca - X_pca.dot(w).reshape(-1,1) * w

    return res
image-20250930170200477

可以发现结果与我们前面求解的一致。

高维数据映射到低维

上面我们已经求解一个数据集的前n个主成分，这些主成分代表的坐标轴的方向，但数据集本身依然是n维的，并没有进行降维。那么具体如何使用PCA方法降维呢？

我们数据$X$ 是一个$mn$ 的矩阵，假设已经求出前数据集的前k个主成分$W_k\in R^{kn}$ 。主成分分析法本质是从一个坐标系转换到另外一个坐标系，原来的坐标系有n个维度的话，转换后的坐标系也有n个维度，只不过对于转换的坐标系来说我们取出前k个，这k个方向更加的重要，那么如何将样本X从n维转换为k维呢？
$$
X=
\begin{pmatrix}
X^{(1)}{1} & X^{(1)}{2} & … &X^{(1)}{n}\
X^{(2)}{1} & X^{(2)}{2} & … &X^{(2)}{n} \
… & … & …\
X^{(m)}{1} & X^{(m)}{2} & … &X^{(m)}{n}
\end {pmatrix} \quad
W_k=
\begin{pmatrix}
W^{(1)}{1} & W^{(1)}{2} & … &W^{(1)}{n}\
W^{(2)}{1} & W^{(2)}{2} & … &W^{(2)}{n} \
… & … & …\
W^{(k)}{1} & W^{(k)}{2} & … &W^{(k)}{n}
\end {pmatrix}\
X.W_k^T=X_k\in R^{m*k}
$$
前面二维的例子中我们是将一个样本和一个$W$ 进行点乘得到了将这一个样本映射到$W$ 这个轴上得到的模的大小，如果将一个样本和k个$W$ 分别做点乘得到一个样本在这k个方向上相应的每一个方向上的大小，那么这k个元素合到一起就能表示一个样本映射到新的k个轴所在的坐标系上相应的样本的大小。

同时对于PCA来说，一旦我们获得了这个$X_k$ ,那么可以相应反过来恢复这个$X$ :
$$
X_k.W_k=X_m\
mk\quad kn\quad m*n\quad\quad
$$
但注意这个$X_m$ 和原始的$X$ 不一样了，降维的过程丢失了一些信息，恢复也是恢复不回来的。

代码封装成类：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
import numpy as np


class PCA:
    
    def __init__(self, n_components):
        assert n_components>=1,"n_components must be valid"
        self.n_components = n_components
        self.components_ = None

    def fit(self, X, eta=0.01, n_iters=1e4):
        assert self.n_components <= X.shape[1],\
        "n_components must not be greater than the feature number of X"

        def demean(X):
            return X - np.mean(X,axis=0)

        def f(w, X):
            return np.sum((X.dot(w)**2))/len(X)

        def df(w, X):
            return X.T.dot(X.dot(w)) * 2./len(X)

        def direction(w):
            return w/np.linalg.norm(w)

        def first_component(X, initial_w, eta, n_iters=1e4, eps=1e-8):

            w = direction(initial_w)
            cur_iter = 0

            while cur_iter < n_iters:
                gradient = df(w, X)
                last_w = w
                w = w + eta*gradient
                w = direction(w)

                if abs(f(w,X)-f(last_w, X)) <eps:
                    break
                cur_iter +=1
            
            return w
        
        X_pca = demean(X)
        self.components_ = np.empty(shape=(self.n_components, X.shape[1]))

        for i in range(self.n_components):
            initial_w = np.random.random(X_pca.shape[1])
            w = first_component(X_pca, initial_w, eta, n_iters)
            self.components_[i,:] = w

            X_pca = X_pca - X_pca.dot(w).reshape(-1,1) *w
        return self
    
    def transform(self, X):
        assert X.shape[1] == self.components_.shape[1]

        return X.dot(self.components_.T)
        
    def inverse_transform(self, X):
        assert X.shape[1] == self.components_.shape[0]

        return X.dot(self.components_)

    def __repr__(self):
        return "PCA(n_components=%d)" % self.n_components

使用代码示例：

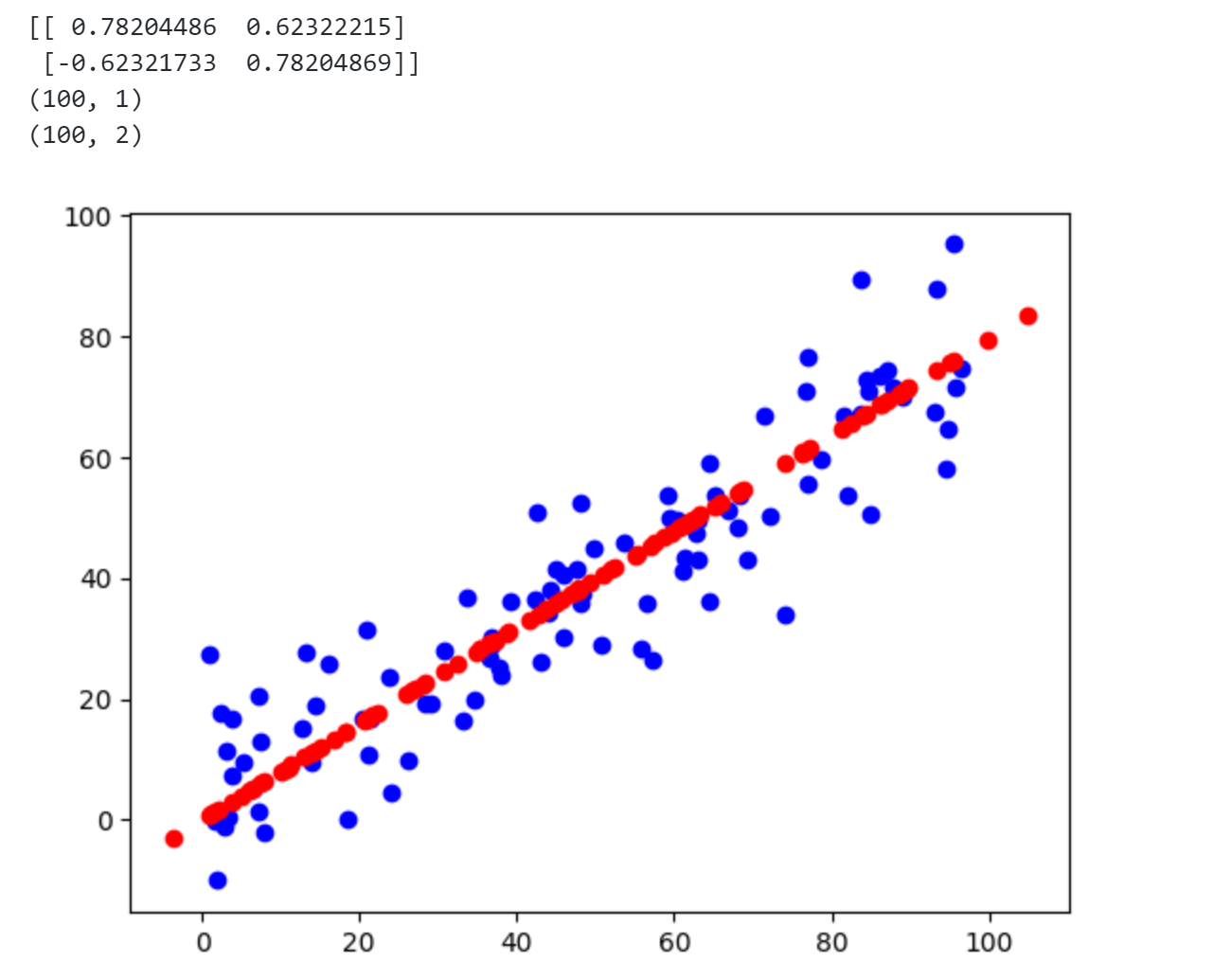
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
import numpy as np
import matplotlib.pyplot as plt
from playml.PCA import PCA

X = np.empty((100,2))
X[:,0] = np.random.uniform(0.,100.,size=100)
X[:,1] = 0.75 * X[:,0] + 3. +np.random.normal(0,10.,size=100) 

pca = PCA(n_components=2)
pca.fit(X)
print(pca.components_)

pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
print(X_reduction.shape)
X_restore = pca.inverse_transform(X_reduction)
print(X_restore.shape)

plt.scatter(X[:,0],X[:,1],c='b')
plt.scatter(X_restore[:,0],X_restore[:,1],c='r')
plt.show()
image-20251005000059266

从上图可发现设定$n_components=2$ 时，两个主成分的结果与前面结果相似。同时设定$n_components=1$ 则数据被降维成1维，同时可以恢复成原来的2维，画到图中如红色的点是恢复的数据，蓝色点是原来的数据，可见这个恢复不能完全恢复。

Scikit-learn中的PCA

代码示例：

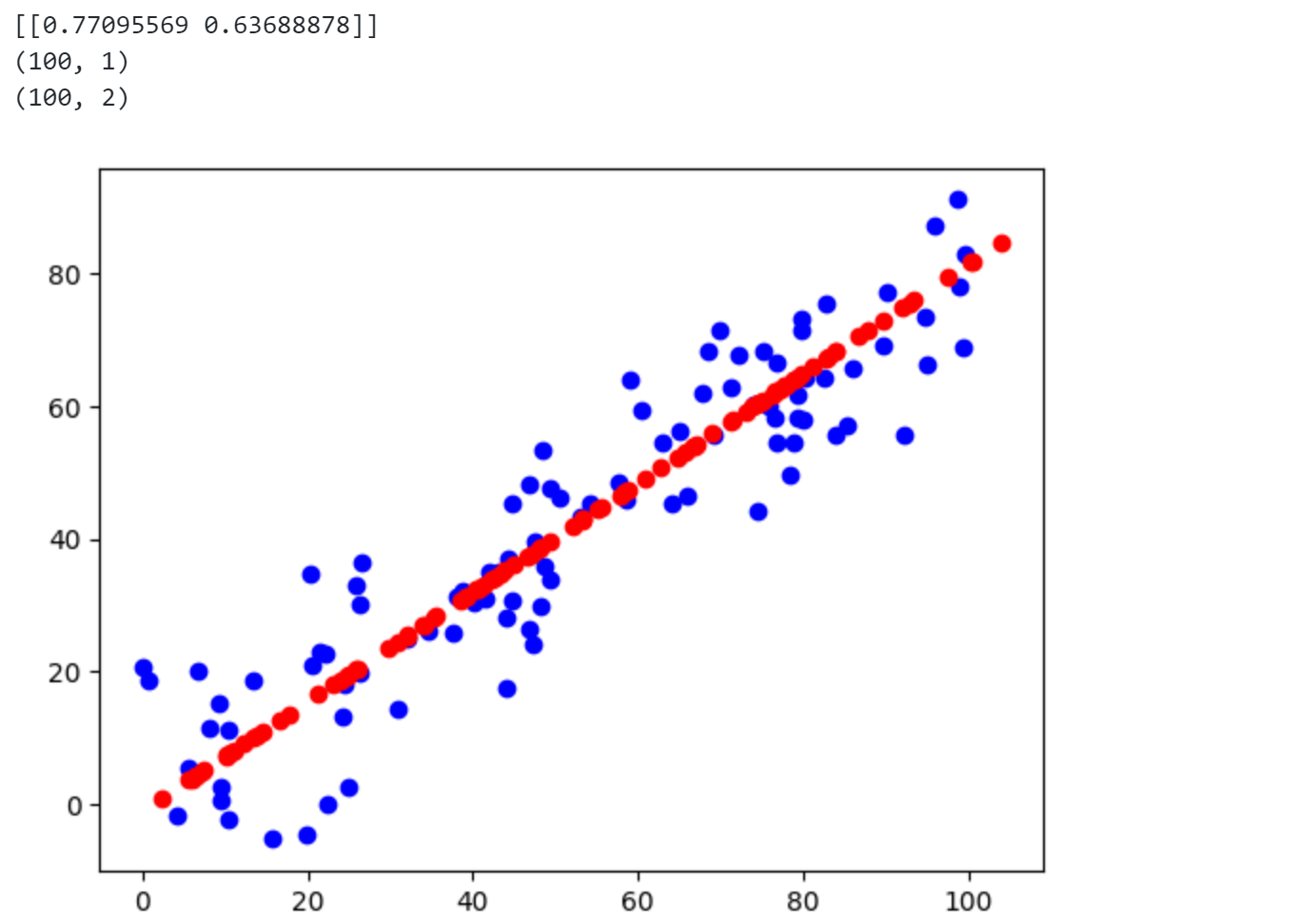
1
2
3
4
5
6
7
8
9
10
11
12
13
14
from sklearn.decomposition import PCA

pca = PCA(n_components=1)
pca.fit(X)

print(pca.components_)
X_reduction = pca.transform(X)
print(X_reduction.shape)
X_restore = pca.inverse_transform(X_reduction)
print(X_restore.shape)

plt.scatter(X[:,0],X[:,1],c='b')
plt.scatter(X_restore[:,0],X_restore[:,1],c='r')
plt.show()
image-20251005181238958

可以发现使用scikit-learn中的pca和之前的结果完全一致。

在真实数据上实验

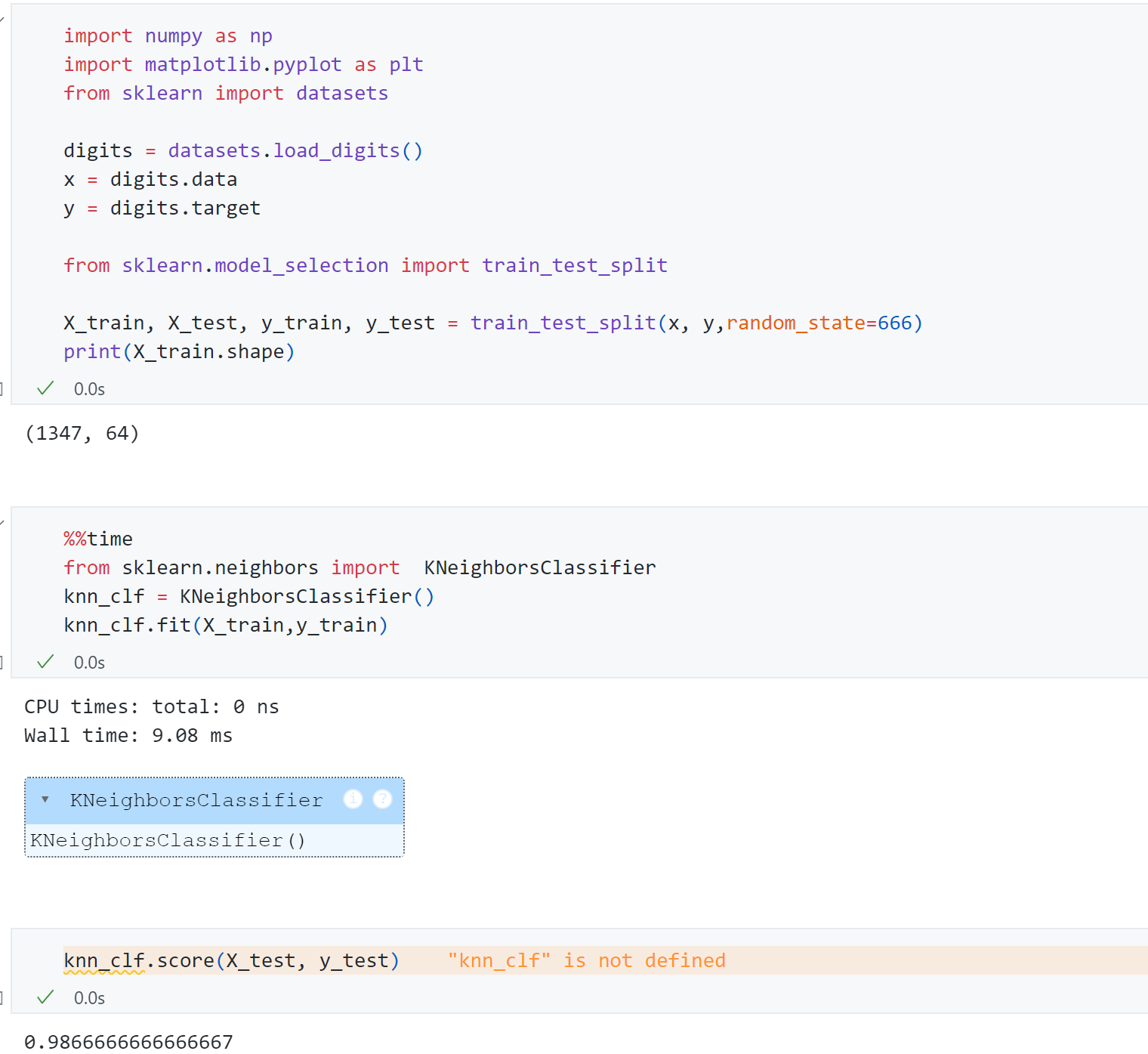
以scikit-learn中的手写数字数据集进行实验：

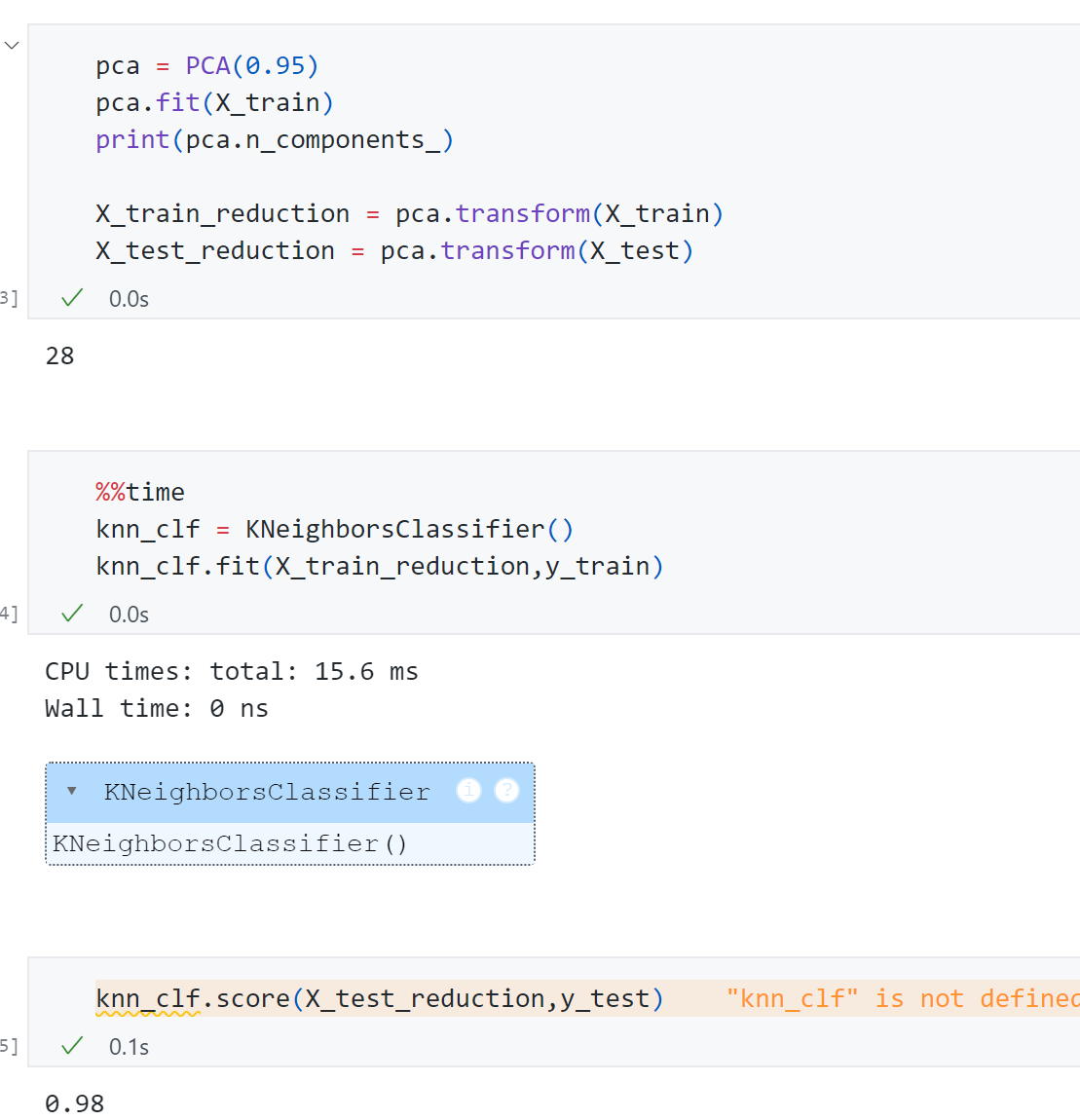
  • 首先使用KNN对原始数据进行分类，可以发现每个数字有64维，训练用时9.08ms,最终测试得分为0.986.
image-20251005185931262
  • 接着使用PCA先对原始数据降维在训练，先测试一下**$n_components=2$**
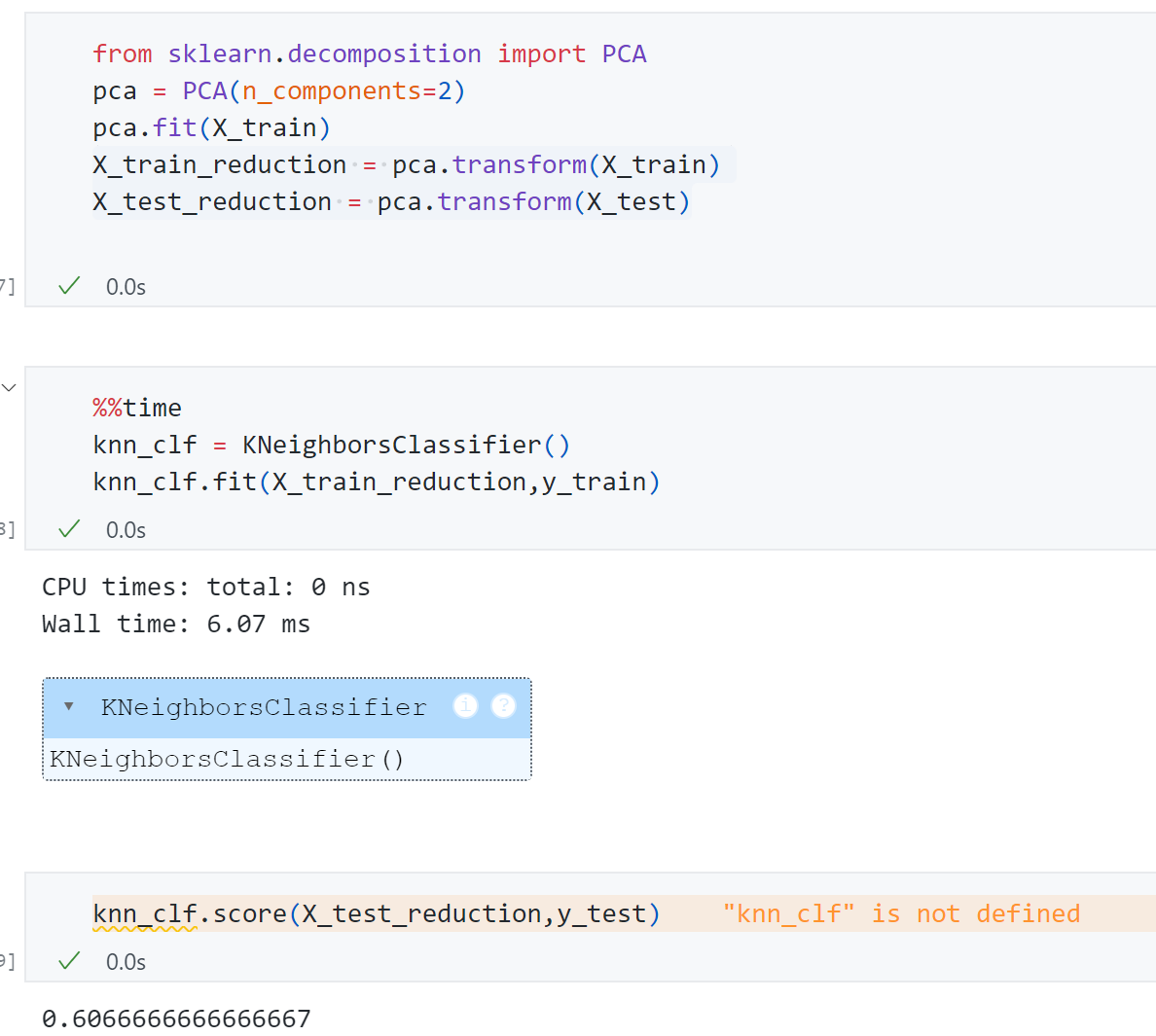
image-20251005190005444

可以发现降维成2维后，精度只有0.60，但是训练时间6.07ms.显然这里降维到10维、20维、30维可能更合适，但具体降到几维呢？一个很容易想到的思路是网格搜索，但是这样也挺麻烦，PCA算法也提供了一个特殊的指标-explained_variance_ratio，用这个指标可以很方便找到对于某个数据集来说多少维合适。

主成分所解释的方差

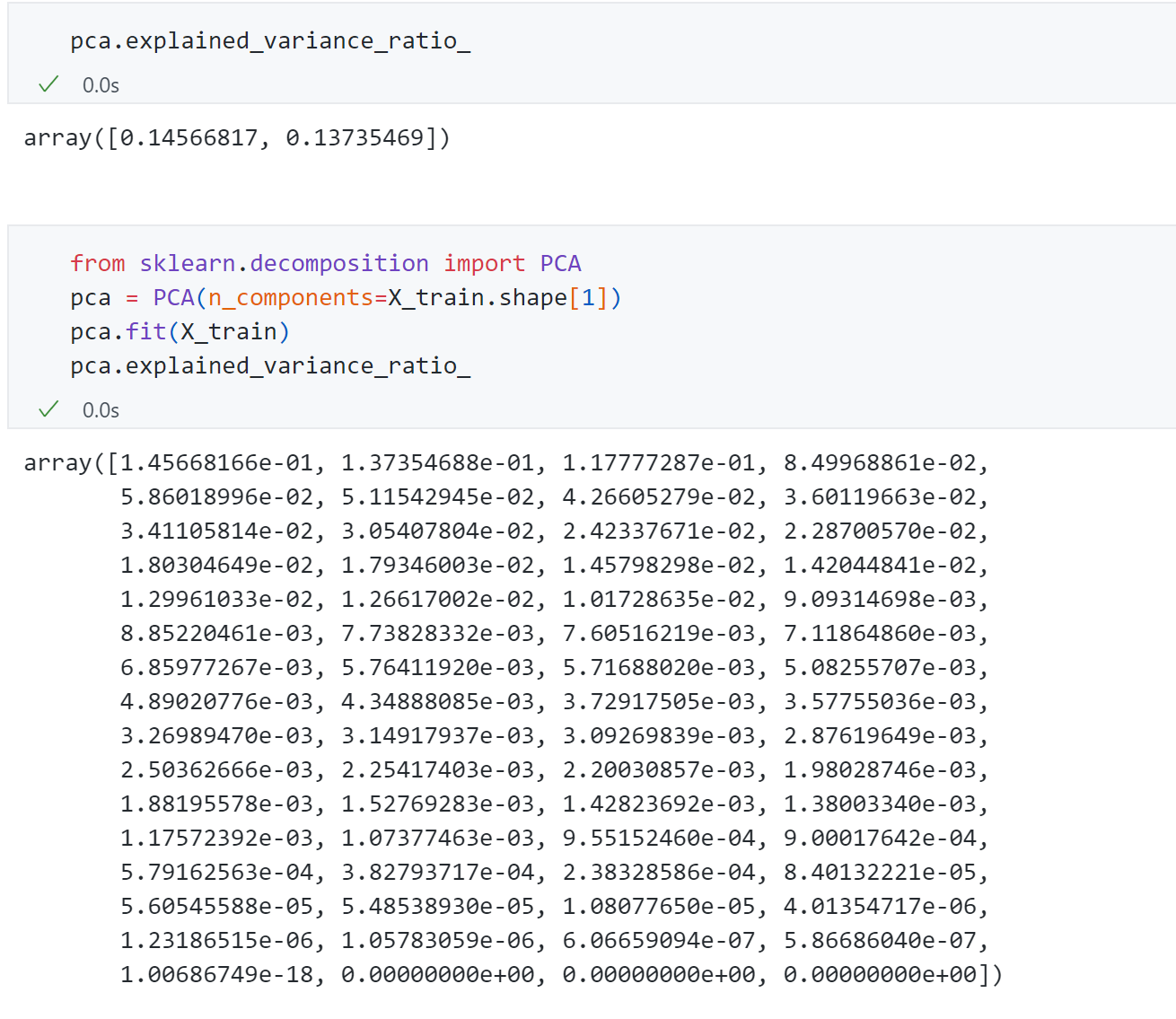
这个explained_variance_ratio指标指的是 解释的方差相应的比例，比如针对上面2维主成分所占比例分别为0.14和0.13，代表这个两个轴分别能解释原数据14%和13%的方差，一共才28%左右，剩下的72%丢失了，丢失的过多，因此我们可以通过这个变量找到我们应该将数据降到多少维。

image-20251005184205198

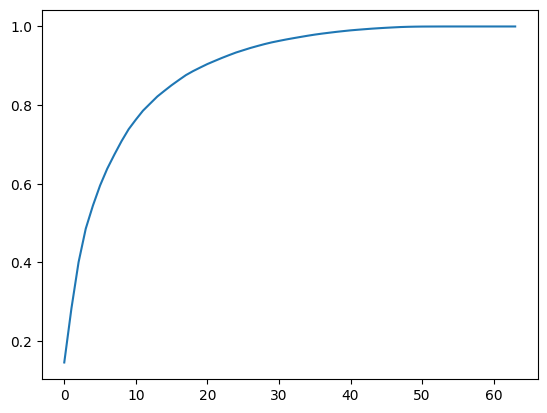
因此将原数据的64维传给PCA重新训练，打印出参数可以发现每个成分所占比例。为了能直观找到多少维度合适，可以将上面的64个主成分所占比例绘制出来：

image-20251005184922785

可以发现取30-40维时方差所占比例一共有80-100之间，因此我们可以通过这个曲线来根据需要来降到多少维度，比如希望保存95%以上信息，可以找95%纵轴对应的横轴是多少维度。同时这个功能也被scikit-learn进行了封装：

image-20251005185807084

可以发现只需要28维就能保存95%以上的信息，同时最终训练精度为0.98，训练时间只需要0ns.

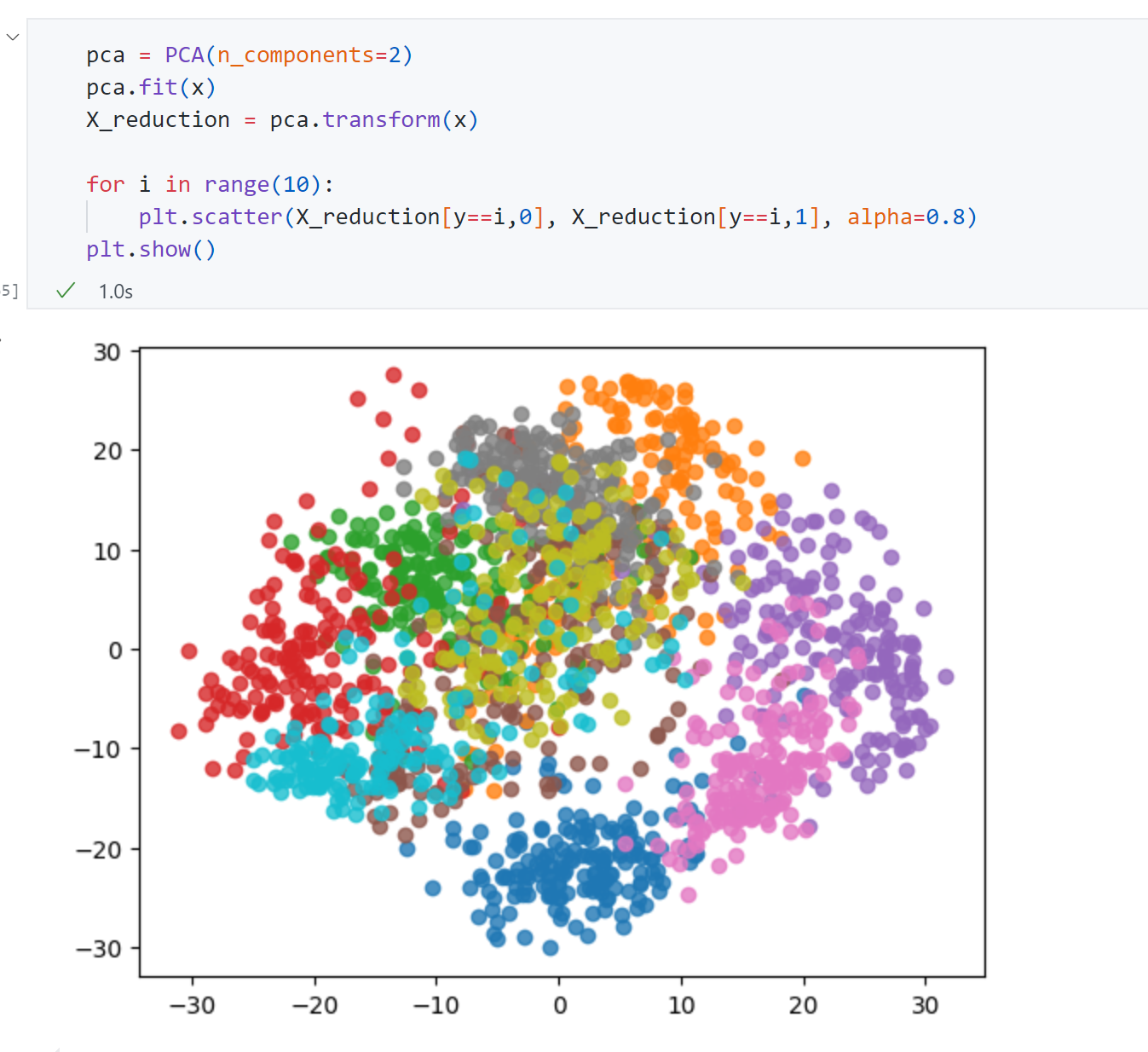
同时数据降到2维也有意义的，那就是可视化：

image-20251005190324594

可以发现2维空间中很多数字的区分度是很明显的，像图中蓝色、粉色、紫色等，如果我只想要区分蓝色数字和紫色数字，显然只需要2维就足够了。

PCA进行降噪

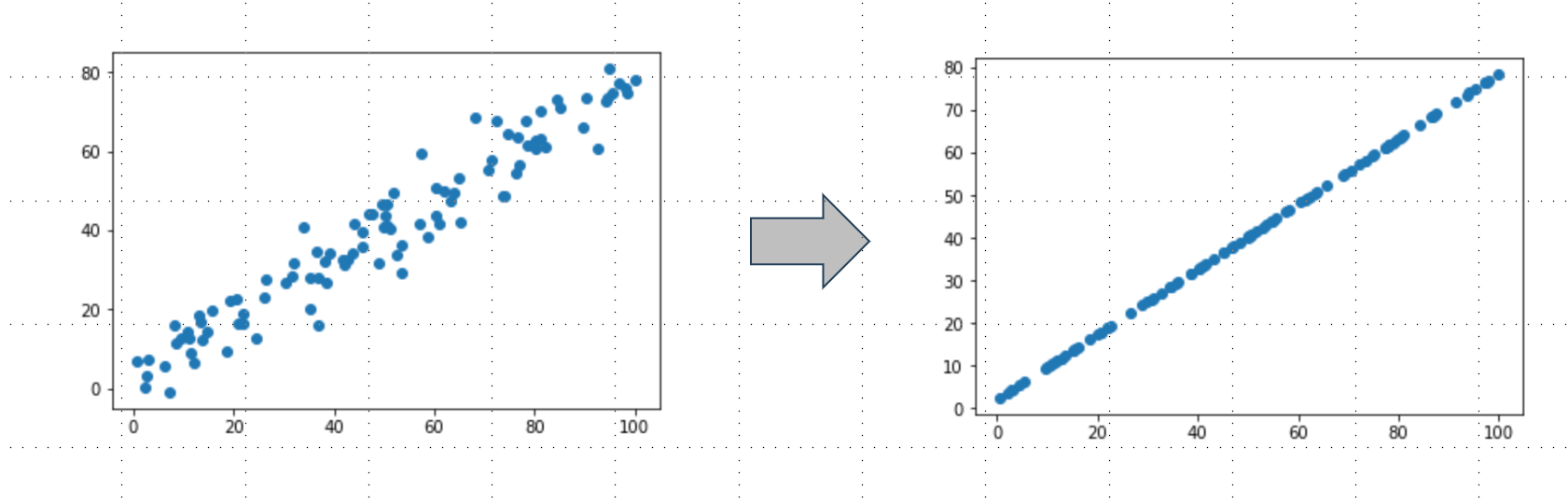
前面对2维数据例子进行了降维如下图，而这个降维的过程可以理解成是去噪。 这个数据集实际情况可能就是右面的直线，这种抖动是噪音，下面数据是我们构造线性关系时时候自己加的噪音，但实际情况我们也不能说明这个抖动全都是噪音，因此也更倾向说从左边数据到右边数据丢失了信息，丢失的信息很有可能一大部分是噪音。

image-20251005200321511

以手写数字为例：

image-20251005200921791

可以发现使用PCA降维后恢复图片明显变了清晰平滑，这里就可以看出PCA的降噪功能。