机器学习(7):多项式回归

Polynomial Regression

什么是多项式回归

前面介绍的线性回归法有一个很大的局限性即要求数据背后是存在线性关系的，但实际中具有很强线性关系假设的数据集很少，更多的数据之间是非线性的关系。而这次要介绍一下使用一种非常简单的手段就可以改进线性回归法使得它可以对非线性的数据进行处理并相应的进行预测，即多项式回归法。同时也引出机器学习一个很重要的概念模型泛化(Model Generalization).

线性回归目的找到一条直线尽可能拟合这些数据，如果数据只有一个特征，那么这个直线可以写成 $y=ax+b$ .而像下图右中的数据虽然可以使用线性回归的方式拟合这种数据，但其具有更加强的非线性关系，因此如果采用一个二次曲线去拟合的话效果会更好。对于二次曲线来说，假设样本只有一个特征，那么相应的方程可以写成 $y=ax^2+bx+c$ 。

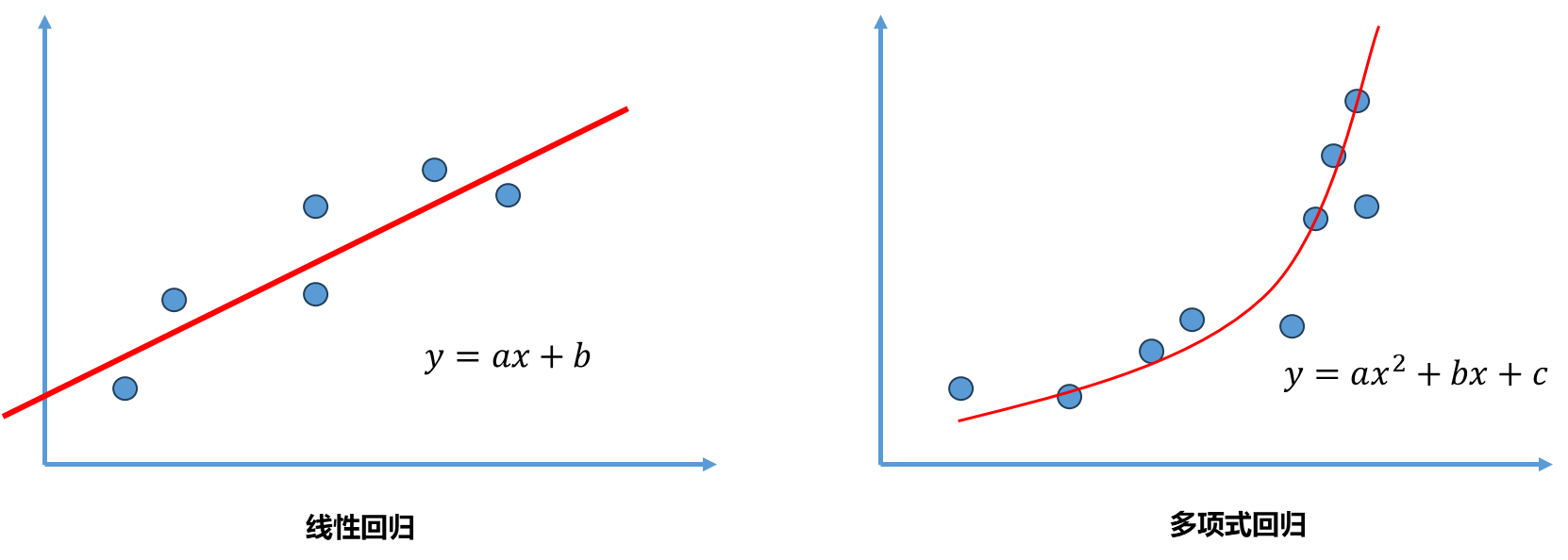
从另外一个角度理解这个二次方程： $x^2$ 看成一个特征， $x$ 理解为另外一个特征。原本数据只有一个特征 $x$ ,现在看成有两个特征的数据集，多了一个特征 $x^2$ ，这样理解的话这个式子依然是一个线性回归的式子，但从x的角度来看还是一个非线性的方程。

简单来说，就是为样本多添加了一些特征，这些特征是原来样本的多项式项，增加了这些特征后我们可以用线性回归更好的拟合这些数据，但本质上是求出了相对于原来特征而言这种非线性的曲线。

编程实现：

先用线性回归拟合

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=(100))

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X, y)
y_pred = lin_reg.predict(X)

plt.scatter(x, y)
plt.plot(x, y_pred,c='r')
plt.show()

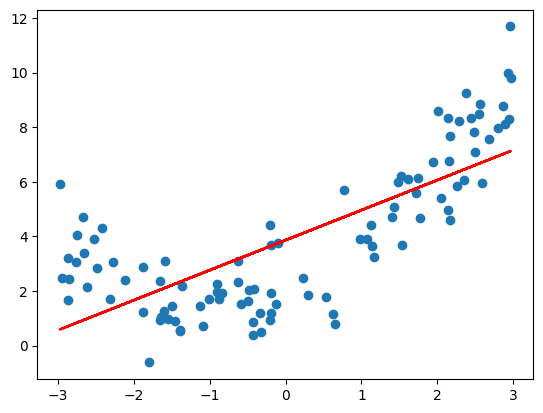
很明显线性回归最终使用一条直线(红线)拟合这样有弧度的曲线，这个拟合效果显然不好。

多项式回归思路：添加一个特征 $x^2$

x2 = np.hstack([X,X**2])

lin_reg2 = LinearRegression()
lin_reg2.fit(x2,y)
y_pred2 = lin_reg2.predict(x2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_pred2[np.argsort(x)],c='r')
plt.show()

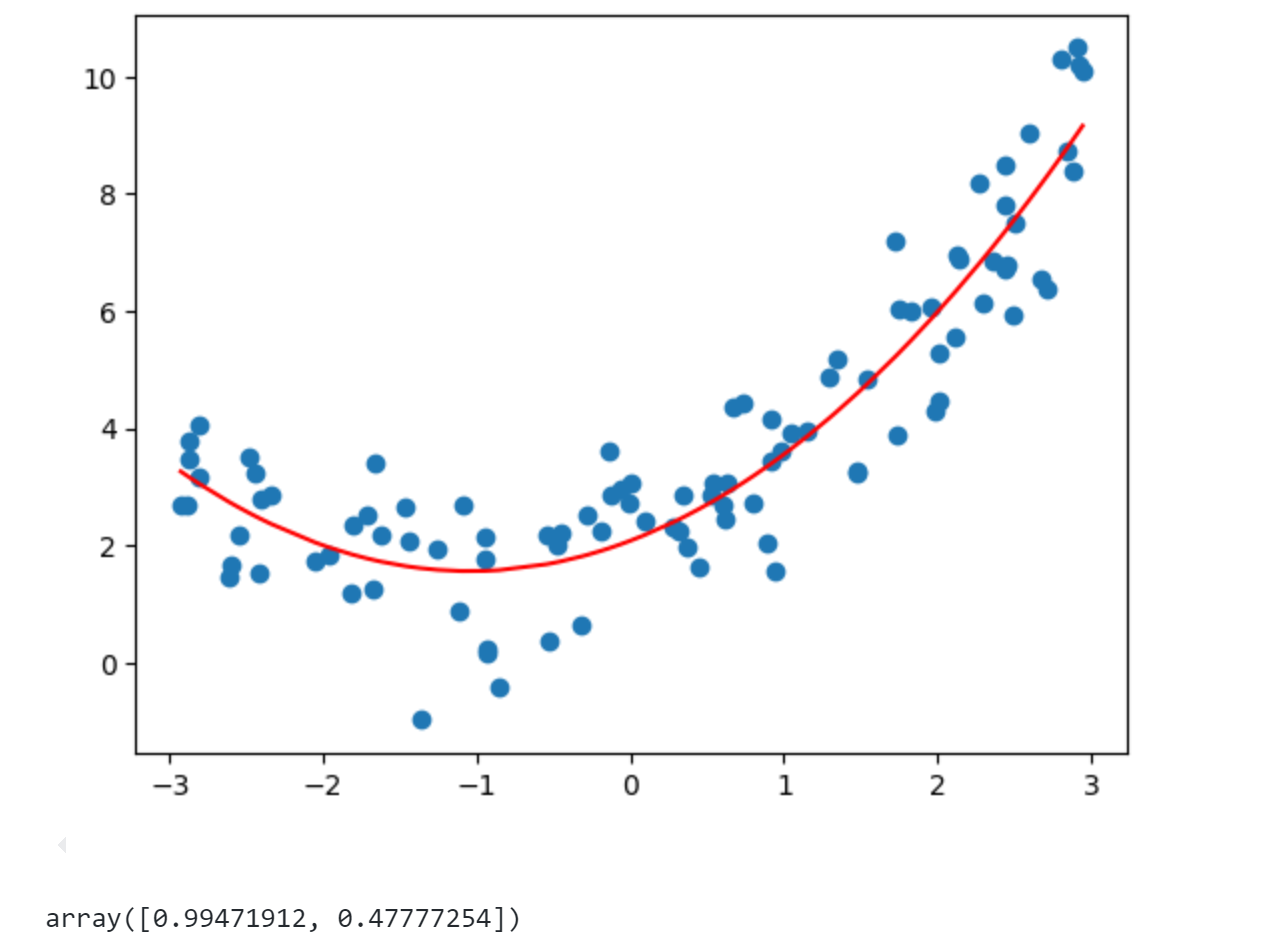
最终得到的系数0.99和0.47与我们构造的1和0.5基本一致。由上面可见多项式回归在机器学习算法上没有新的地方，完全是使用线性回归的思路，它的关键在于为原来的数据样本添加新的特征，而得到新特征方式是原有的特征的多项式组合，采用这种方式就可以解决一些非线性问题。上篇讲的PCA是对数据降维处理，而这里的多项式回归是对数据升维度使得算法可以更好拟合高纬度数据。

scikit-learn中的多项式回归

采用与上面中一样的随机数据

import numpy as np
import matplotlib.pyplot as plt

x = np.random.uniform(-3, 3, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0, 1, 100)

上面使用多项式回归时是相当于对数据 $X$ 添加了特征，因此scikit-learn中多项式回归被封装在了preprocessing这个包中.。

from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree=2)
poly.fit(X)
X2 = poly.transform(X)

$degree=2$ 相当于最多添加了2次幂的特征,观察一下此时 $X_2$ 的形状及具体内容：

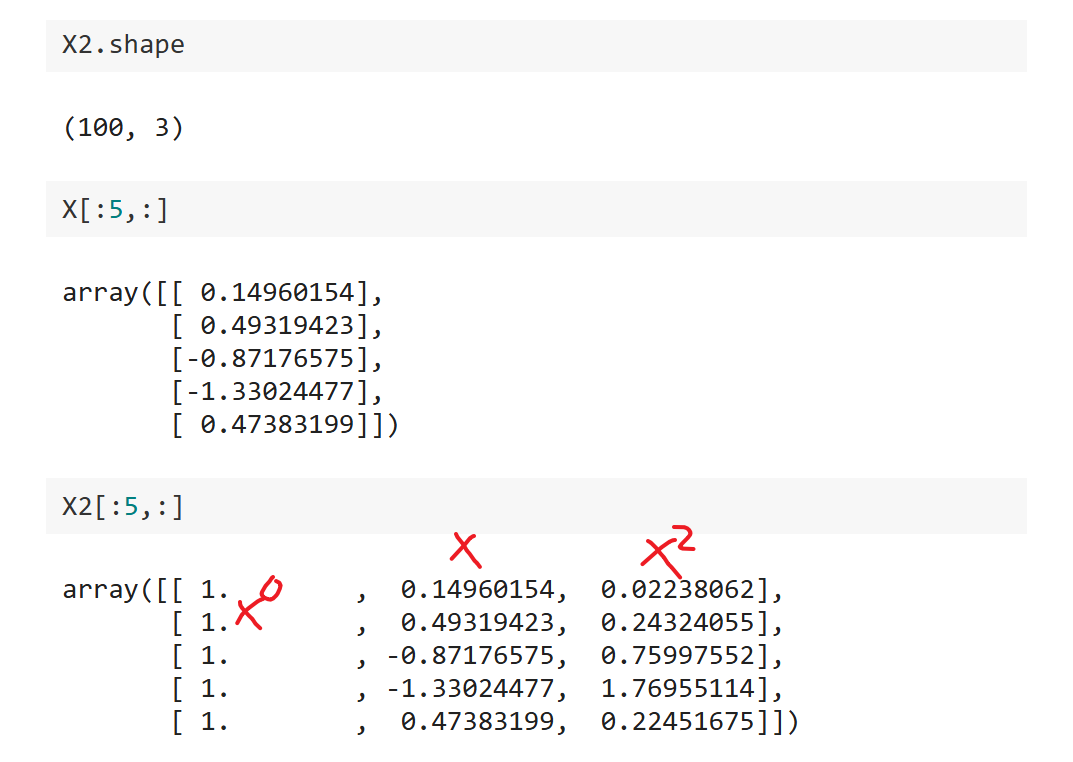
可以发现此时是一个100*3的矩阵，可以发现第一列全是1相当于 $x^0$ ,第二列是 $x$ ，第三列是 $x^2$ .

接着使用线性回归进行预测：

from sklearn.linear_model import LinearRegression

lin_reg = LinearRegression()
lin_reg.fit(X2,y)
y_pred = lin_reg.predict(X2)

plt.scatter(x, y)
plt.plot(np.sort(x), y_pred[np.argsort(x)], color='r')
plt.show()

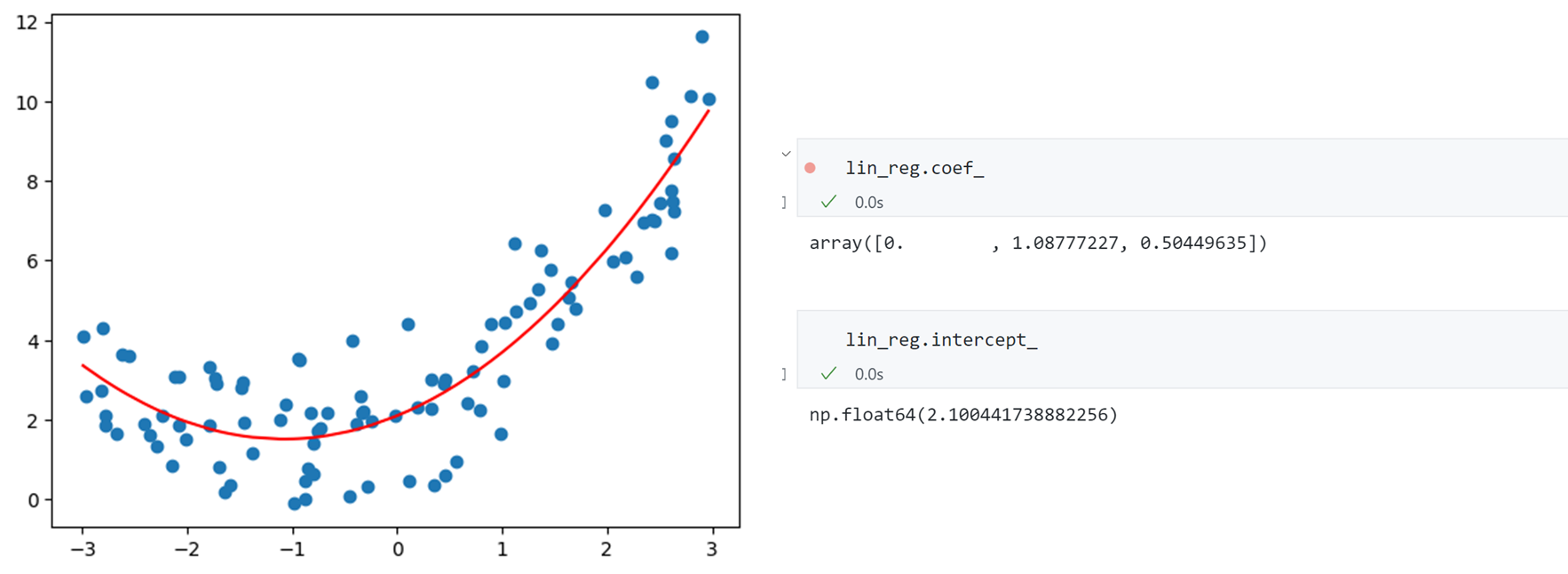
同时观察得到三个特征的系数分别为0,1.08,0.5，截距为2.10，与我们的构造数据的系数基本一致。

前面的数据构造时 $X$ 只有一个特征，我们来看看 $X$ 有两个特征的情况：

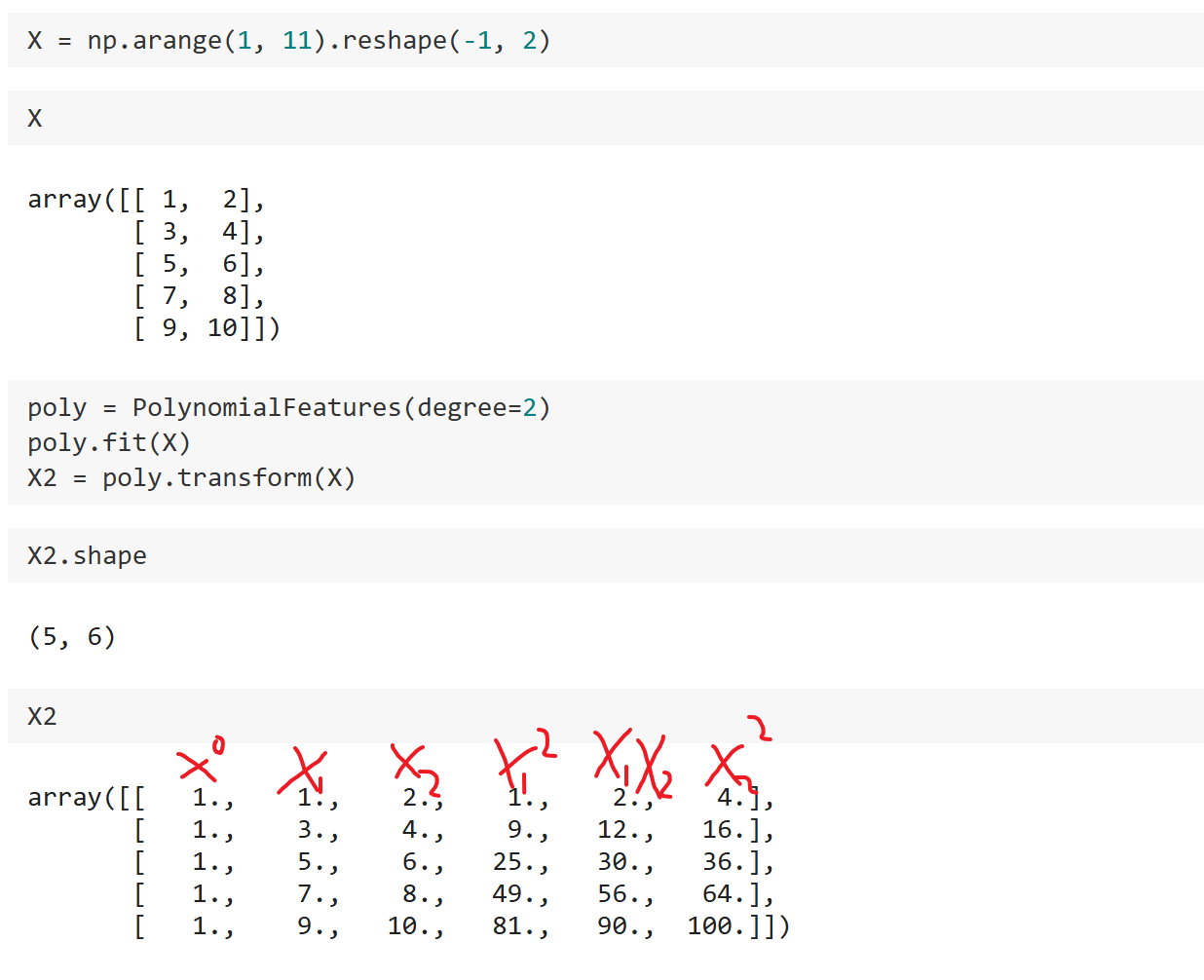
可以发现此时最终的 $x_2$ 有6个特征，分别是0次方，和两个特征的1次方，以及两个特征组合的2次方。

同理如果 $degree=3$ ，则有：

$x_1,x_2-->1,x_1,x_2\\ \quad\quad\quad\quad\quad\quad\quad x_1^2,x_2^2,x_1,x_2\\ \quad\quad\quad\quad\quad\quad\quad\quad\quad x_1^3,x_2^3,x_1^2x_2,x_1x_2^2$

Pipeline

采用pipeline的方式写多项式回归：

x = np.random.uniform(-3,3,size=100)
X = x.reshape(-1,1)
y = 0.5 * x**2 + x + 2 + np.random.normal(0,1,size=100)

from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

poly_reg = Pipeline([
    ("poly",PolynomialFeatures(degree=2)),
    ("std_scaler",StandardScaler()),
    ("lin_reg", LinearRegression())
])

poly_reg.fit(X,y)
y_pred = poly_reg.predict(X)

plt.scatter(x, y)
plt.plot(np.sort(x), y_pred[np.argsort(x)],c='r')
plt.show()

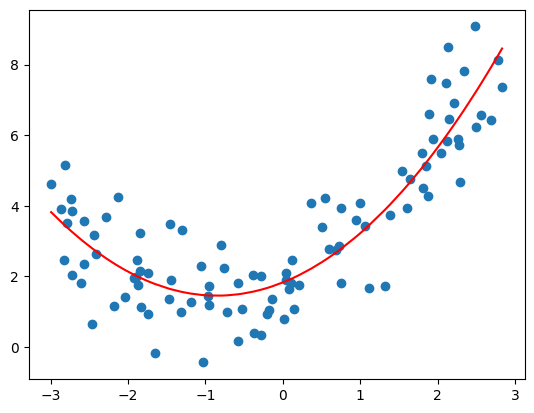
过拟合与欠拟合

通过多项式回归我们可以轻松对非线性的数据进行拟合，进而求解回归问题。但是过渡的使用将会牵扯到机器学习领域一个非常重要的问题----过拟合和欠拟合。

前面已经试用过线性回归方式拟合数据集得到 $r^2$ 只有0.42，这个值相对较低，所以直接使用线性回归的方式不太合适。多项式回归本质上是增加样本数据特征之后依然使用线性回归，我们也可以使用 $r^2$ 这个指标来衡量多项式回归好坏。我们先对比一下使用线性回归(左)和多项式回归( $degree=2$ )（右）两者的结果：

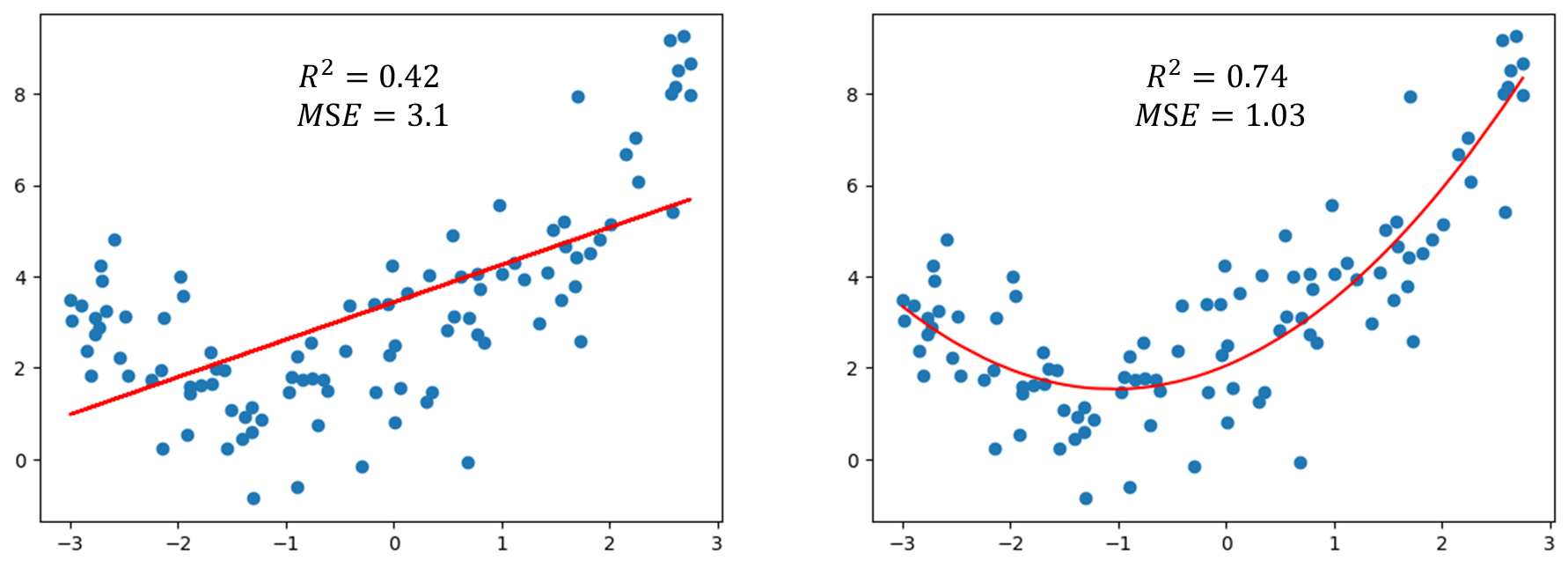
可以发现采用 $degree=2$ 的多项式回归结果 $R^2=0.74,MSE=1.03$ 要比单纯线性回归好很多。

那么如果变大 $degree$ 结果会怎么样呢？

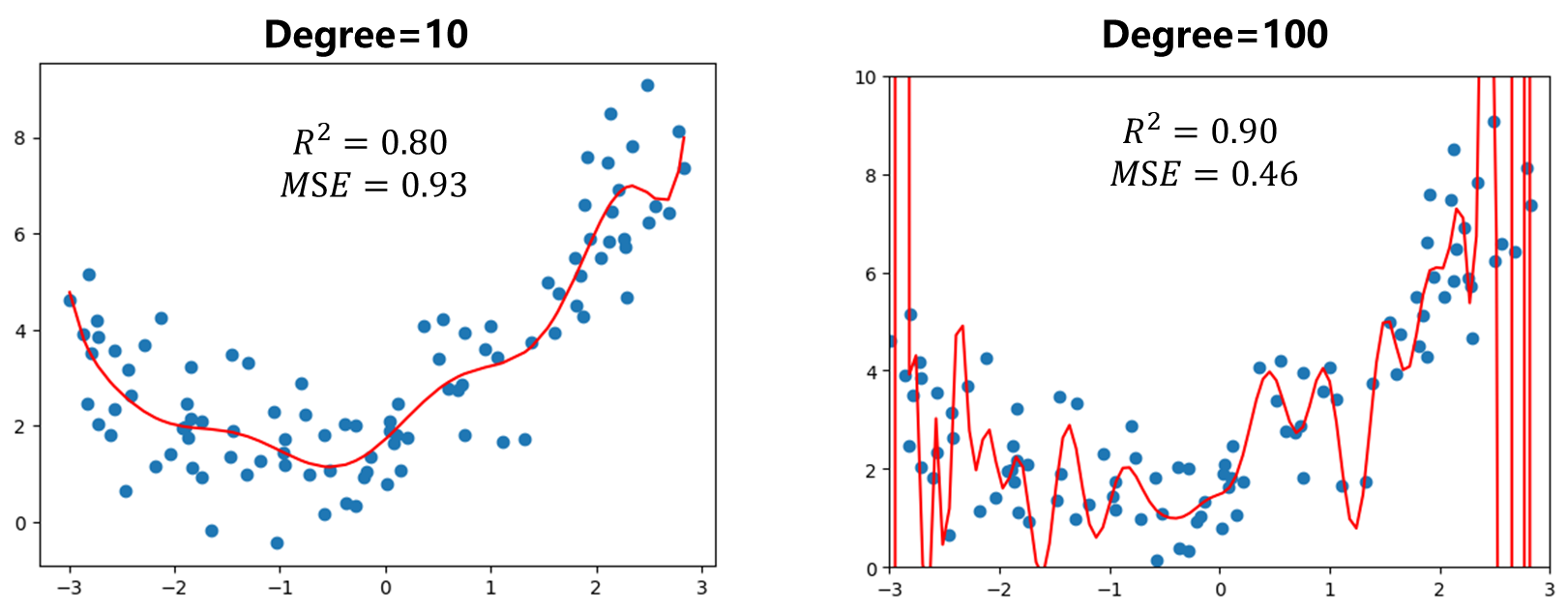
可以发现指标 $R^2,MSE$ 变得更好了，随着 $degree$ 增高，我们一定能找到一根曲线能够使得所有样本点在这根曲线上，最终使得 $MSE=0$ .但是这真的能反映样本数值走势吗？显然不是。就是图 $Degree=100$ 时此时明显过拟合了overfitting.而上面线性回归时我们只是用一根直线拟合我们的数据，这种方式也没有很好反映样本数据的特征，但它的错误时太过简单了，这种情况称为欠拟合即underfitting.

欠拟合指算法所训练的模型不能完整表述数据关系。过拟合指算法所训练模型过多表达了数据间的噪音关系。

从上面的图示例可以发现多项式回归能够很直观的解释过拟合和欠拟合现象。

为什么要有训练数据集与测试数据集

机器学习主要解决的问题是过拟合问题，再来观察一下上面 $degree=10$ 的情况：假如有一个新的样本点如紫色的点，这个预测的结果显然跟原本蓝色的样本点不在一个趋势上，直观上就会感觉这个预测结果是错误的。

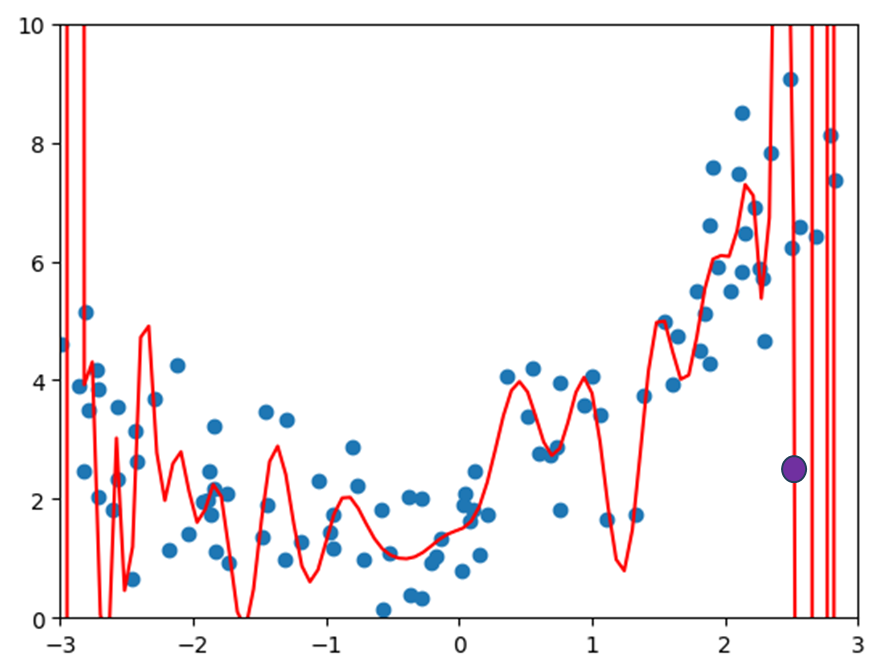
换句话说就是在过拟合这种场景下，虽然曲线将原先的样本点拟合的较好，但是一旦来了新的样本点，它就不能进行很好的预测了，这种情况下称得到的模型泛化能力是非常弱的。我们训练模型为的不是最大程度拟合这些点，而是为了获得一个可以预测的模型，当有新的样本点数据时模型可以给出很好的解答，正因如此，我们去衡量模型对于训练数据的拟合程度有多好是没有意义的，我们真正需要的是模型的泛化能力有多好，因此这种情况下该如何做呢？

很简单就是采用训练测试数据集的分离即–train-test-spilt.如果使用训练数据得到的模型在测试数据上效果也很好的话，那可以说模型泛化能力是很强的。

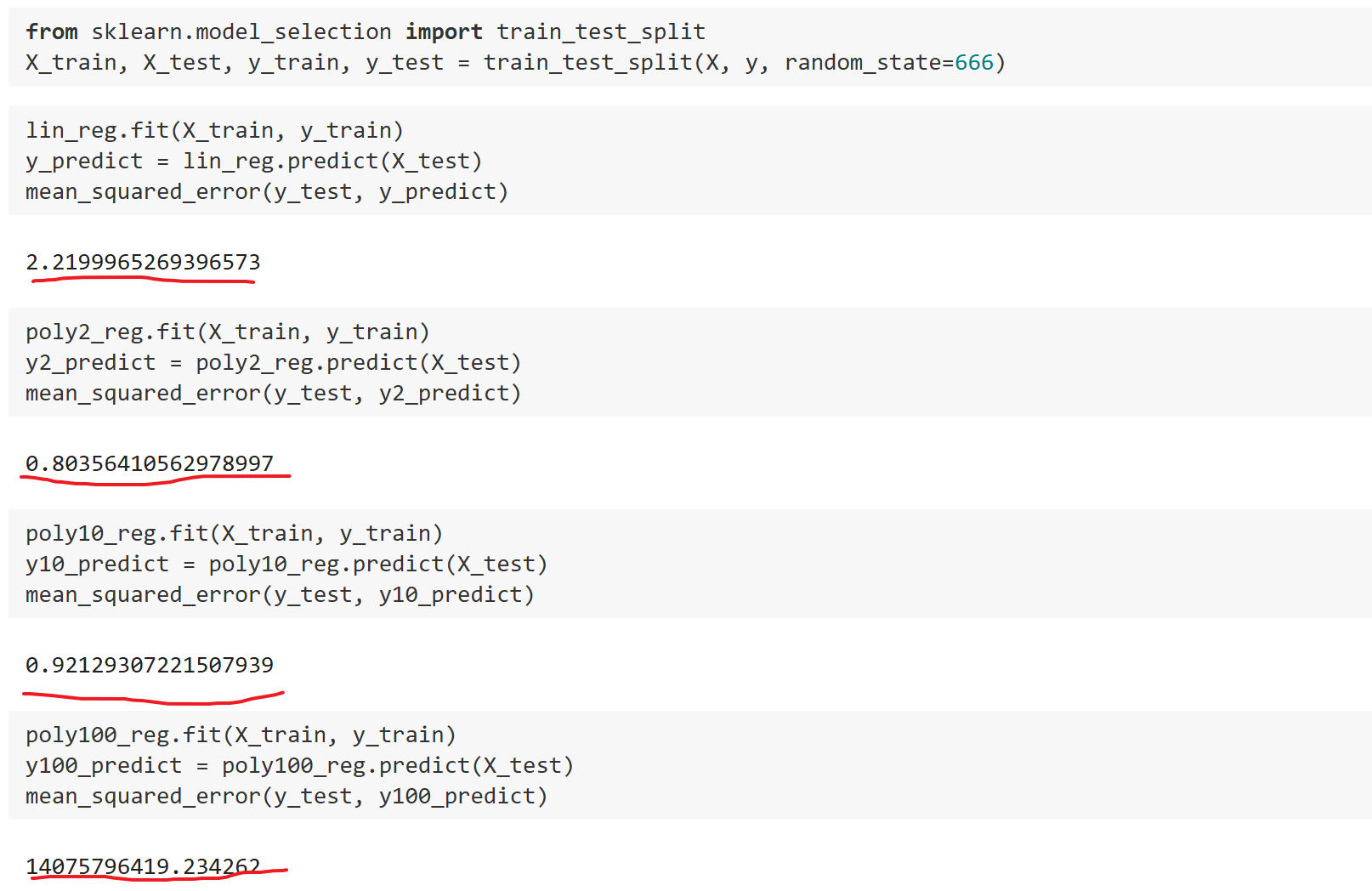
可以发现使用 $degree=2$ 时的模型在测试数据上MSE最小，泛化能力最强，而 $degree=10$ 次之， $degree=100$ 则是尤其大。

学习曲线

随着训练样本的逐渐增多，算法训练出的模型的表现能力。

首先绘制一下线性回归模型的学习曲线：

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=10)

from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error

train_score = []
test_score = []

for i in range(1, 76):
    lin_reg = LinearRegression()
    lin_reg.fit(X_train[:i], y_train[:i])

    y_train_predict = lin_reg.predict(X_train[:i])
    train_score.append(mean_squared_error(y_train[:i], y_train_predict))
    
    y_test_predict = lin_reg.predict(X_test)
    test_score.append(mean_squared_error(y_test, y_test_predict))
    
plt.plot([i for i in range(1, 76)], np.sqrt(train_score), label="train")
plt.plot([i for i in range(1, 76)], np.sqrt(test_score), label="test")
plt.legend()
plt.show()

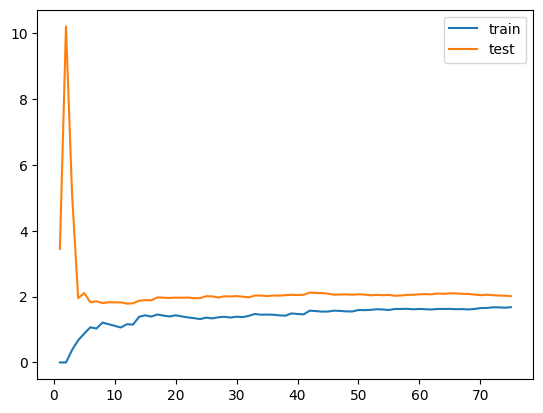
从趋势上看，误差随着训练数据集的增加不断升高，即训练数据越多越难拟合所有的数据。而测试数据是一个下滑的曲线，刚开始样本较少时，误差很大，训练样本多到一定程度时，测试误差减少到一定稳定的情况。最终训练误差和测试误差大体是在一个级别上的，到那时测试误差还是高一些，因为泛化会多一些误差。

同理绘制多项式回归 $degree=2$ 的曲线：

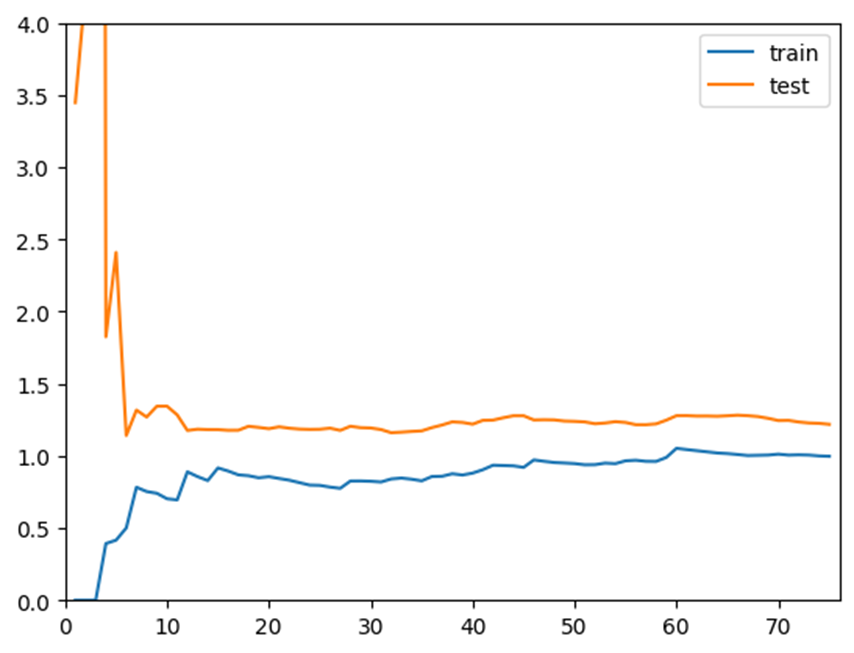
可以发现整体趋势上与线性回归是一致的，训练曲线上升到一定程度稳定，测试曲线下降到一定程度稳定。但是多项式回归最终稳定的误差位置相对比较低，说明二阶多项式回归的结果是比较好的。

同理绘制多项式回归 $degree=20$ 的曲线：

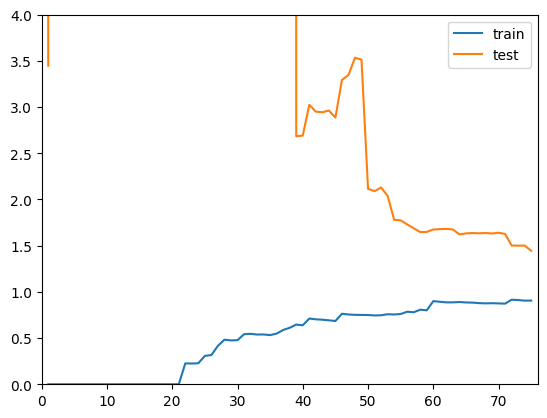
可以发现整体趋势上依然是一致的，训练曲线上升到一定程度稳定，测试曲线下降到一定程度稳定。但是两根曲线在相对稳定的位置间距比较大，说明模型在训练数据上拟合比较好，但是在测试数据上误差依然很大。这种情况通常就是过拟合的情况。

综合比较一下三种曲线：

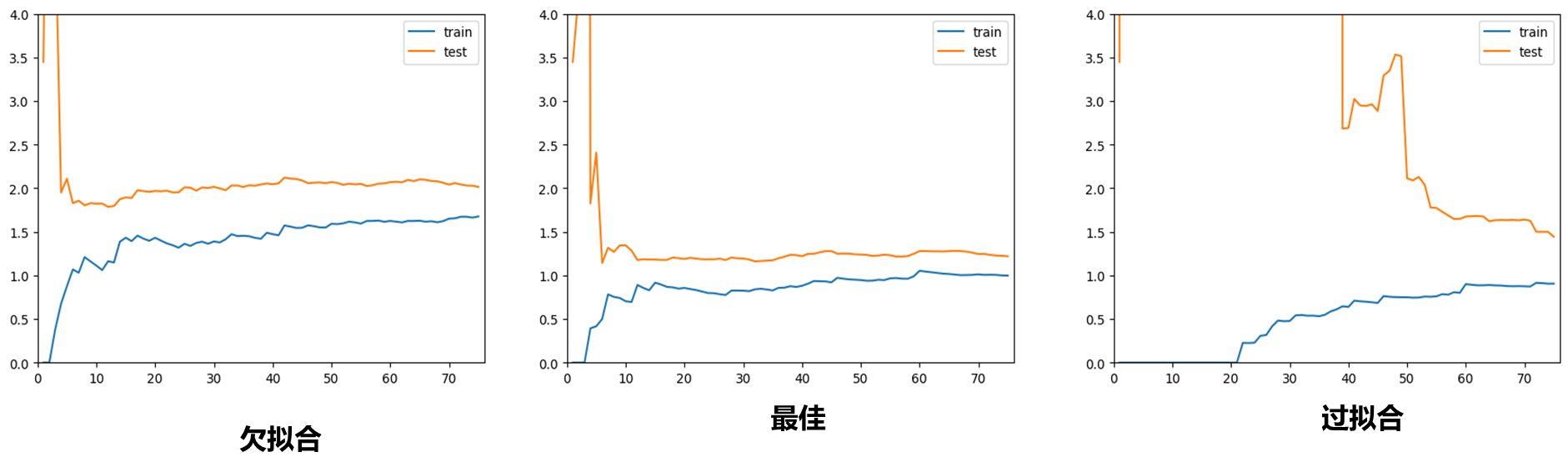
对于欠拟合的情况和最佳的情况相比较，训练和测试趋于稳定的位置比最佳情况趋于稳定的位置要高一些，说明无论对于训练数据集还是测试数据集，相应的误差都比较大，这是因为本身模型不对。而过拟合情况，在训练数据集上相应的误差不大，但是测试数据集误差比较大，说明模型此时泛化能力不够好。

通过上面学习曲线的方式能够进一步深刻理解过拟合、欠拟合。