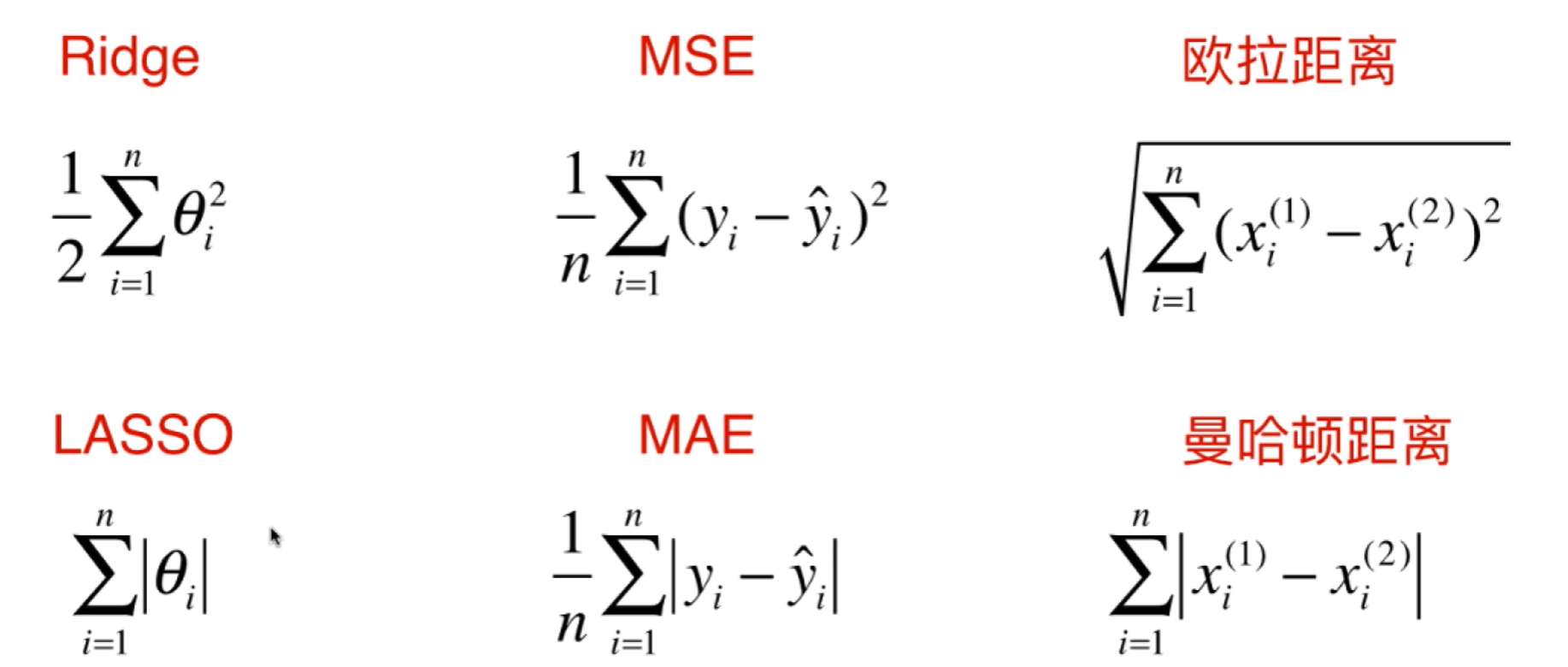Model Generalization

验证数据集与交叉验证

上篇通过过拟合和欠拟合的概念明白了为什么要做train-test-split。但这样其实也有一个问题就是模型会针对特定测试数据集过拟合.我们在想办法找到一组参数，这组参数使得训练数据集得到的模型在测试数据上效果最好，由于测试数据集是已知的，我们相当于针对这组测试数据集调参。

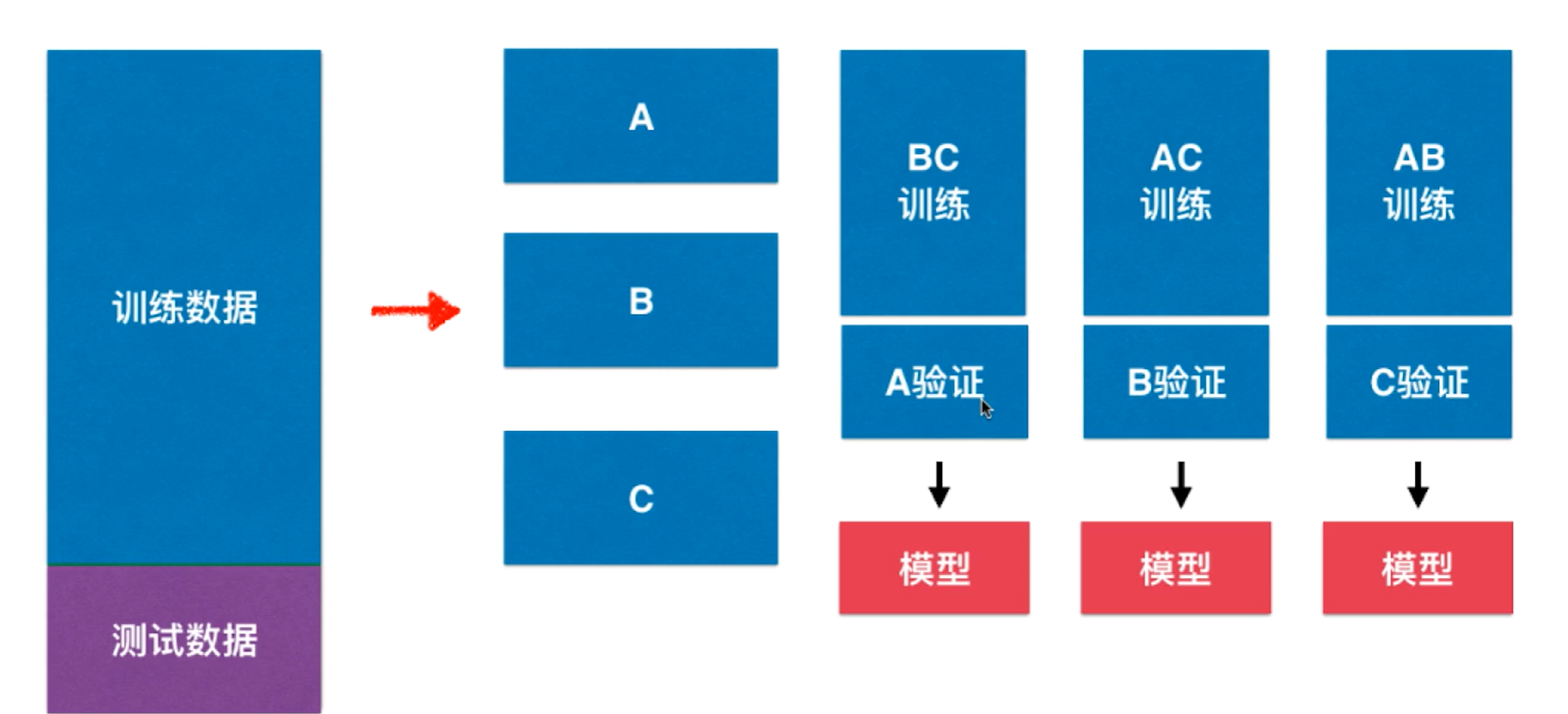
如何解决这个问题呢？将数据进一步分为三部分：训练集、验证集、测试集。训练集依然用来训练模型，而验证数据集是做之前测试数据集做的事情，训练好模型后将验证数据送给模型看看相应效果是怎么样的，直到模型针对验证数据已经达到最优了。最后再把测试数据给这个最优的模型，这样得到模型最终的性能。

其中训练集、验证集参与了模型的创建，而测试集是完全不可知的。测试数据集是作为衡量最终模型性能的数据集，而验证集是调整超参数使用的数据集。

但还是有一个问题就是随机。因为每一次验证的数据集都是随机的从原来的数据切出来的，而训练的模型有可能过拟合验证数据集，但是只有一份验证数据集，一旦验证数据集里有相应比较极端的数据就可能导致模型相应的不准确。为了解决这个问题就有了交叉验证(Cross Validation).

如何理解交叉验证呢？

image-20251012011900955

如上图，对于训练数据通常分成k份，比如上图中分为三份A,B,C.接下来将A,B,C分别作为验证数据集，而剩下的合起来作为训练数据集，这样一来可以得到3个模型，这3个模型每一个在验证数据集都会求处一个性能指标，最终平均作为衡量标准。实际中可以分为k个模型，k个模型的均值作为结果调参，也被称为k-folds cross validation.

编程实现：

  • 首先加载一下digits数据集，然后采用train-test-split方式手动网格寻找knn最优参数
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import numpy as np
from sklearn import datasets
from sklearn.model_selection import train_test_split

digits = datasets.load_digits()
X = digits.data
y = digits.target

X_train, X_test, y_train, y_test = train_test_split(X, y,test_size=0.4, random_state=666)

from sklearn.neighbors import KNeighborsClassifier

best_k, best_p, best_score = 0, 0, 0
for k in range(2,11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        knn_clf.fit(X_train, y_train)
        score = knn_clf.score(X_test, y_test)

        if score > best_score:
            best_k, best_p, best_score = k, p, score

print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

得到结果为：Bestk=3;BestP=2;BestScore=0.986Best\quad k =3;Best\quad P =2;Best\quad Score =0.986

  • 采用交叉验证的方式
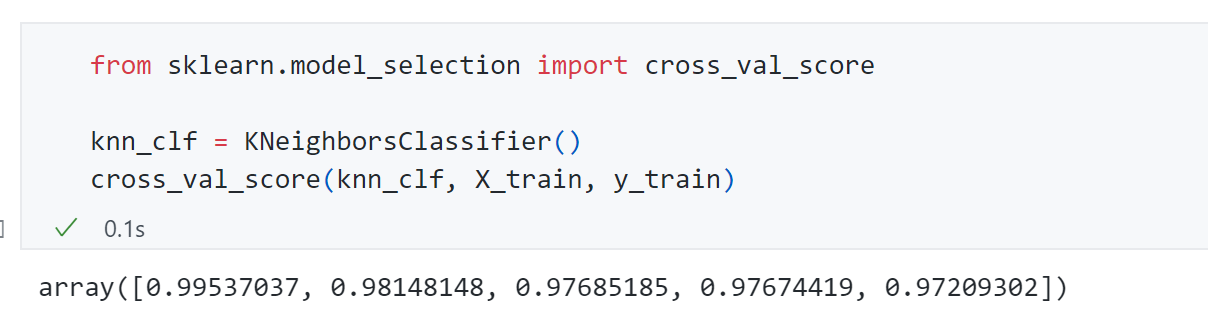
image-20251012144909950

可以发现cross_val_score默认将X_train分成了5份，上面5个数值就是5份交叉验证得到的结果。

1
2
3
4
5
6
7
8
9
10
11
12
best_k, best_p, best_score = 0, 0, 0
for k in range(2, 11):
    for p in range(1, 6):
        knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=k, p=p)
        scores = cross_val_score(knn_clf, X_train, y_train)
        score = np.mean(scores)
        if score > best_score:
            best_k, best_p, best_score = k, p, score
            
print("Best K =", best_k)
print("Best P =", best_p)
print("Best Score =", best_score)

同样接下来采用交叉验证的方式调参得到Bestk=2;BestP=2;BestScore=0.985Best\quad k =2;Best\quad P =2;Best\quad Score =0.985，与前面采用train-test-split方式进行比交，可以发现得到的k不同，但我更倾向交叉验证这种方式的结果，因为前面train-test-split方式和有可能过拟合了分离出来的测试集。其次可以发现交叉验证得到的分数0.985略小于前面train-test-split得到的0.986，因为交叉验证不会过拟合某一组的测试数据，平均下来分数会稍微低一些。

但我们交叉验证是为了拿到最好的kk 和pp ，至于具体模型泛化能力如何我们需要在测试集上测试：

1
2
3
best_knn_clf = KNeighborsClassifier(weights="distance", n_neighbors=2, p=2)
best_knn_clf.fit(X_train, y_train)
best_knn_clf.score(X_test, y_test)

因此最终得到score=0.9805score=0.9805, 此时模型分类准确度是98%.

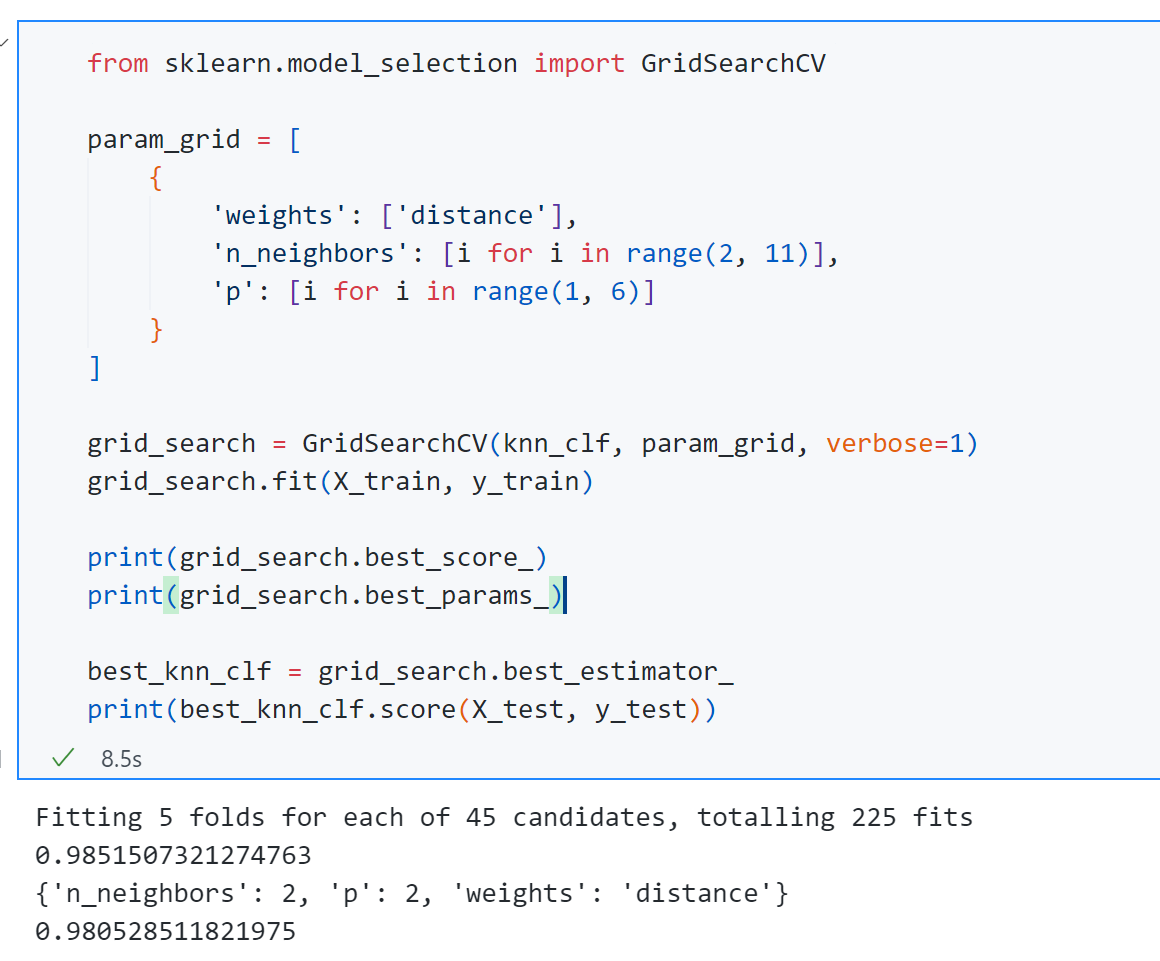
同时这整个过程在前面将KNN算法时已经提到过了网格搜索：

image-20251012150128825

这个GridSearchCV中的“CV"代表的就是Cross Validation交叉验证的意思，可以发现通过网格搜索得到的kk 和pp 和我们前面的一致。这个"Fitting 5 folds for each for 45 candidates" 就是因为每一次使用交叉验证的方式，交叉验证将训练集分为了5份，而参数组合为9∗5=459*5=45 种情况，一共就是225次训练。

既然cross_val_score函数默认将训练集分为5份，如何修改呢？只需要传入一个cv参数，传入想要的值即可。

1
2
cross_val_score(knn_clf, X_train, y_train, cv=5)
grid_search = GridSearchCV(knn_clf, param_grid, verbose=1, cv=5) # 网格搜索也可以传入cv参数

最后谈一下交叉验证的缺点：每次要训练k个模型，相当于整体性能慢了k倍.但这样找到的参数可以更加的信赖。

极端情况下这种k-folds cross validation可以变成一种留一法LOO-CV(Leave -One- Out Cross Validation),即每次把训练数据分成m份，m-1份用于训练，剩下一份用来验证。这样做将完全不受随机的影响最接近模型的性能指标，同样缺点计算量巨大。

首先明白什么是验证数据集，进而引出交叉验证的方法，通过交叉验证的方式来寻找最佳的参数，使用这样的参数进行模型训练通常最大程度遏制训练的模型出现过拟合或者欠拟合。

偏差方差权衡 Bias Variance Trade off

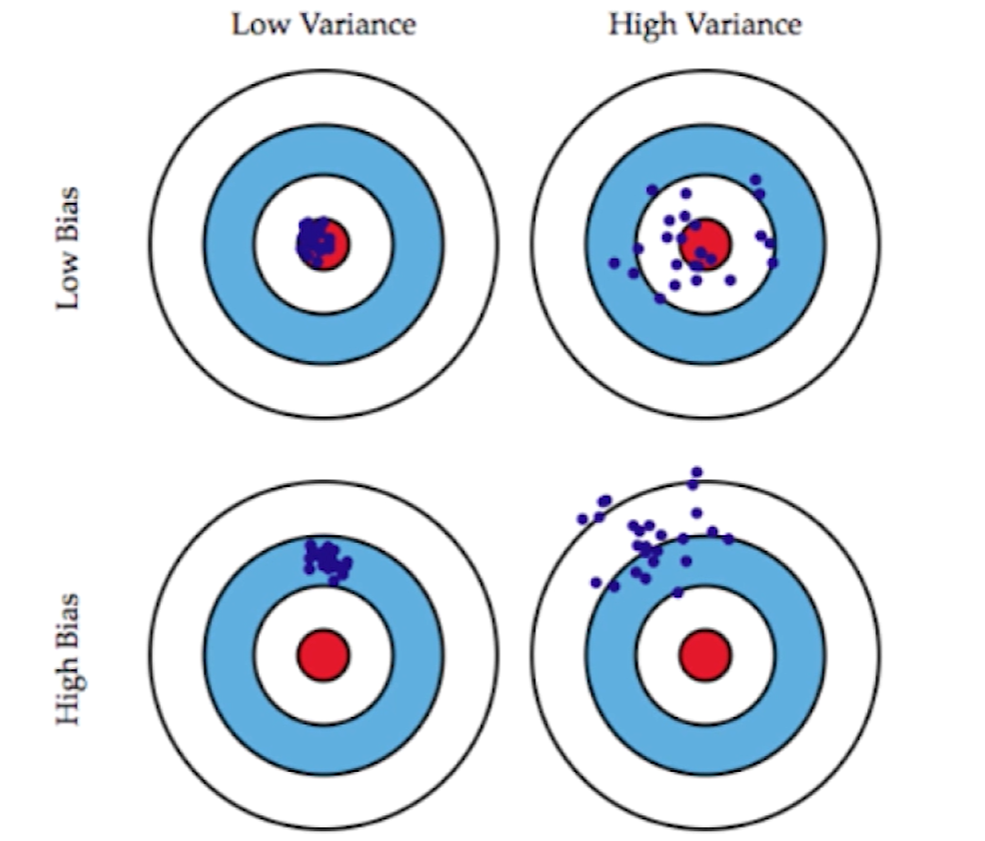
先来看看什么是偏差和方差：

image-20251012172242731

先以左下角的图片为例，我们目标中心是这个红点，但是所有的点(紫色点）都偏离了这个中心的位置，这种情况就叫做偏差。接着观察右上角的图片，紫色点都围绕在红点周围，没有偏差，但是整体太过分散不集中，所有有非常高的方差。

机器学习过程中，我们实际训练的模型都是要预测一个问题，而这个问题本身就可以理解为这个靶子中心，而我们根据数据来拟合这个模型进而预测这个问题就如图中紫色点打出去的枪，而模型就有可能犯偏差和方差两种错误。

所以一般模型的误差来源三方面：

模型误差=偏差（Bias）+方差(Variance)+不可避免的误差模型误差=偏差（Bias）+方差(Variance) +不可避免的误差

而导致偏差的主要原因：对问题本身的假设不正确！比如上篇针对非线性数据使用线性回归方法。欠拟合就是这样一个例子。

而针对方差：数据的一点点扰动都会较大地影响模型，通常原因使用的模型太复杂比如高阶多项式回归。过拟合就是个例子。

同时有些算法天生就是高方差的算法比如KNN,非参数学习通常都是高方差算法，因为不对数据进行任何假设。而有些算法天生就是高偏差算法，比如线性回归。参数学习通常都是高偏差算法，因为对数据具有极强的假设。

大多数算法具有相应的参数可以调整偏差和方差，比如KNN种的K,线性回归中使用多项式回归。

偏差和方差通常是矛盾的：降低偏差会提高方差，降低方差会提高偏差。而机器学习算法主要挑战来自于方差，解决高方差的手段主要如下：

  • 降低模型复杂度
  • 减少数据维度：降噪
  • 增加样本数
  • 使用验证集

模型泛化与岭回归

解决过拟合问题或者解决模型含有较大方差误差的问题，有一种很标准的处理手段-模型正则化(Regularization).

以线性回归问题为例：

目标：使得∑i=1m(y(i)−θ0−θ1X1(i)−θ2X2(i)−...−θnXn(i))尽可能小目标：使J(θ)=MSE(y,y^;θ)尽可能小目标：使得\sum_{i=1}^{m}(y^{(i)}-\theta_0 -\theta_1X_1^{(i)}-\theta_2X_2^{(i)}-...-\theta_nX_n^{(i)})尽可能小\\ 目标：使J(\theta)=MSE(y,\hat{y};\theta)尽可能小

但此时如果过拟合会导致θ\theta 系数特别大，如何限制呢？

加入模型正则化，目标：使J(θ)=MSE(y,y^;θ)+α12∑i=1nθi2尽可能小加入模型正则化，目标：使J(\theta)=MSE(y,\hat{y};\theta)+\alpha\frac{1}{2}\sum_{i=1}^{n}\theta_i^2尽可能小

这种后面加入参数项的正则化方式通常也称为岭回归(Ridge Regression)。

编程实现：

  • 数据准备
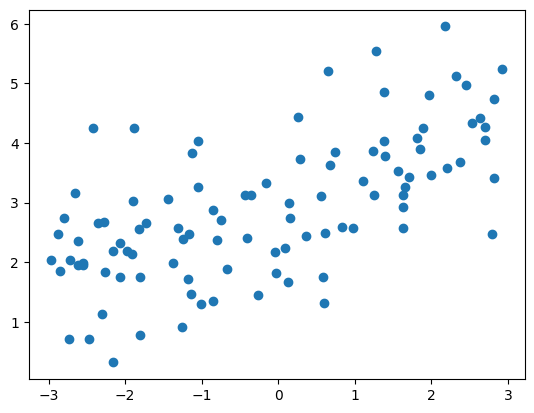
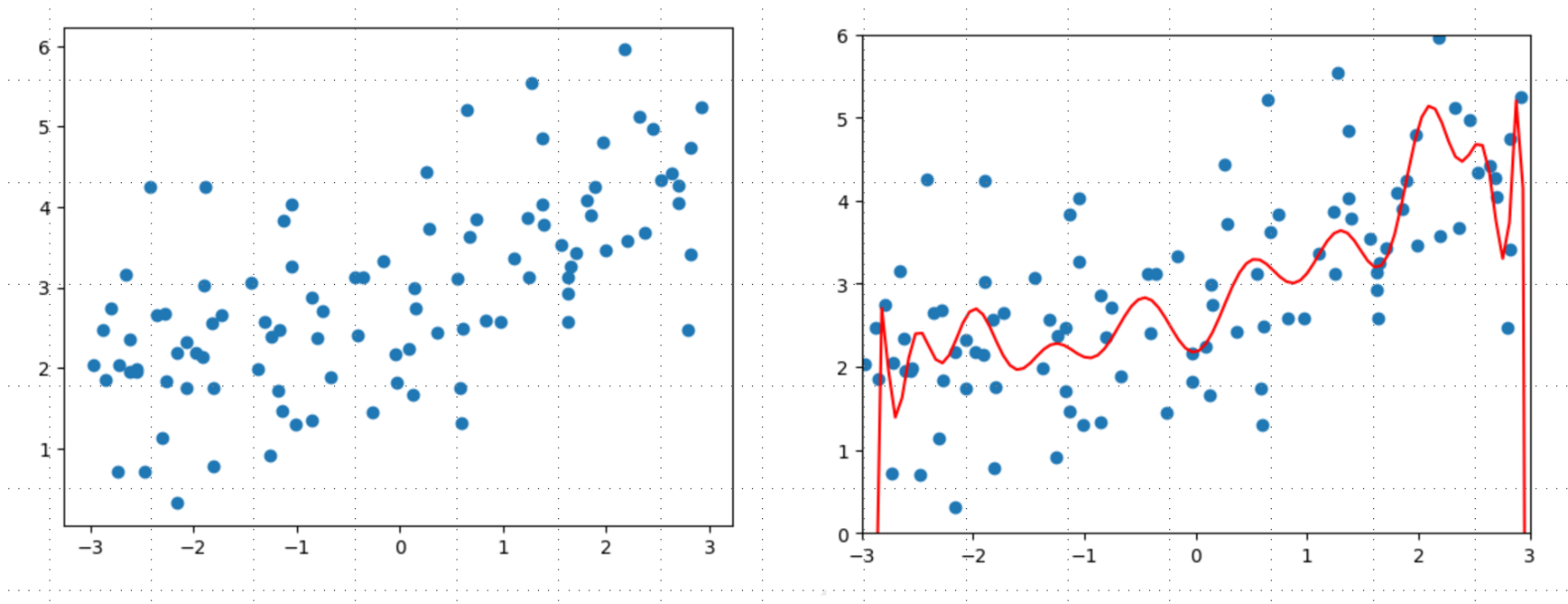
1
2
3
4
5
6
7
8
9
10
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)

plt.scatter(x, y)
plt.show()

image-20251012184605780

  • 采用degree=20的多项式回归
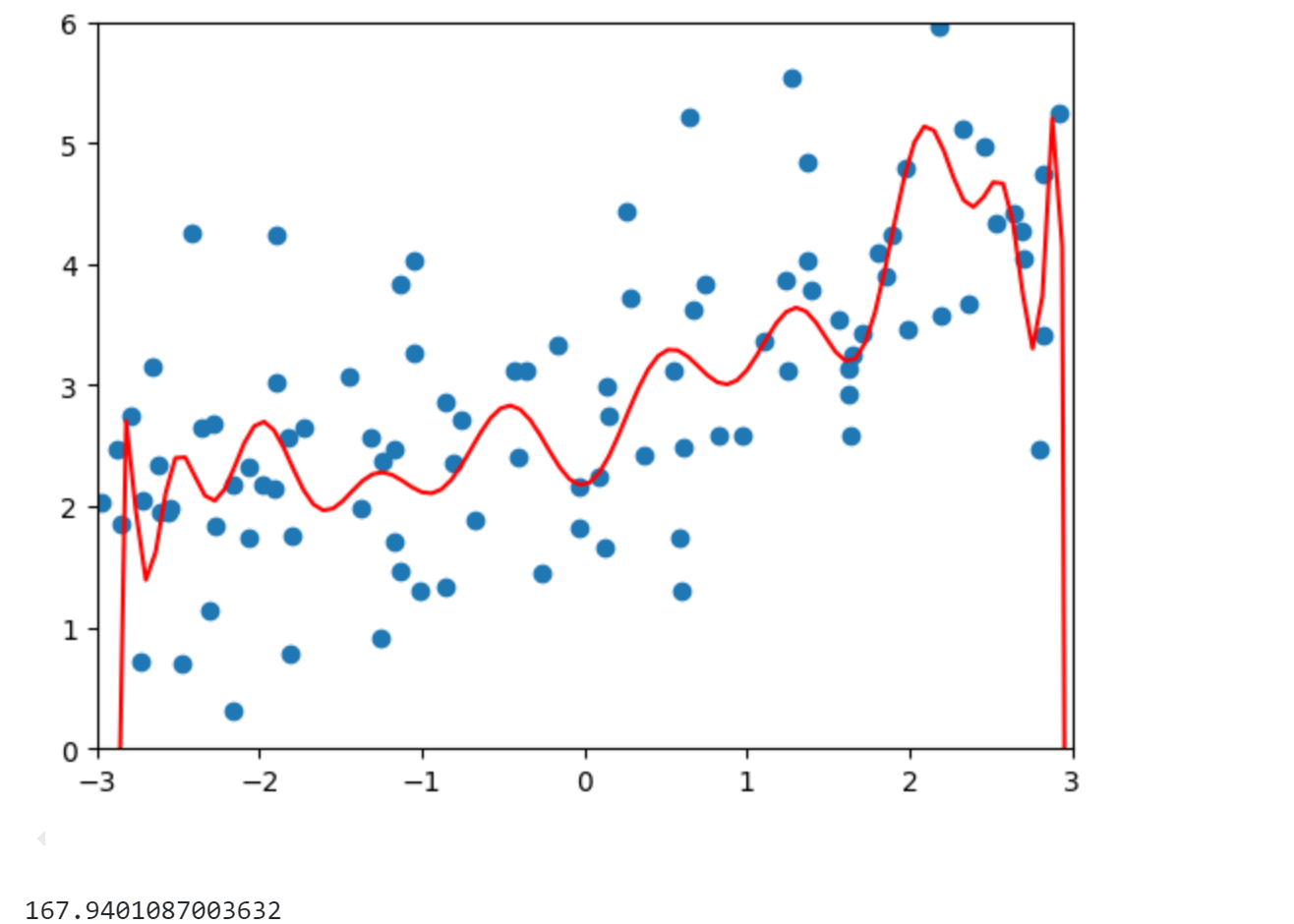
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression

def PolynomialRegression(degree):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lin_reg", LinearRegression())
    ])
    
from sklearn.model_selection import train_test_split

np.random.seed(666)
X_train, X_test, y_train, y_test = train_test_split(X, y)

from sklearn.metrics import mean_squared_error

poly_reg = PolynomialRegression(degree=20)
poly_reg.fit(X_train, y_train)

y_poly_predict = poly_reg.predict(X_test)
print(mean_squared_error(y_test, y_poly_predict))

X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
y_plot = poly_reg.predict(X_plot)

plt.scatter(x, y)
plt.plot(X_plot[:,0], y_plot, color='r')
plt.axis([-3, 3, 0, 6])
plt.show()
image-20251012184916531

可以发现模型MSE为167，明显过拟合了。

  • 采用岭回归
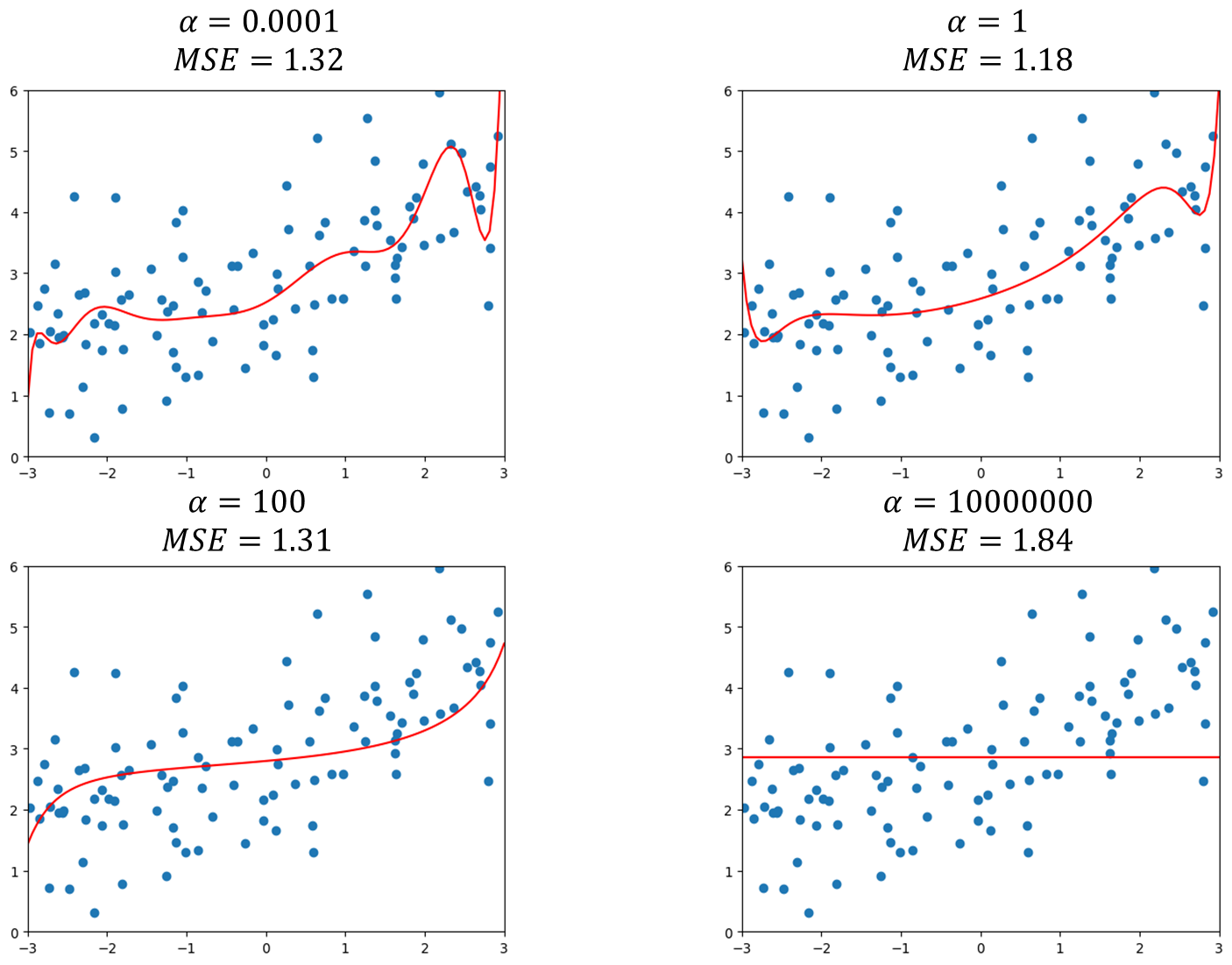
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
from sklearn.linear_model import Ridge

def RidgeRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("ridge_reg", Ridge(alpha=alpha))
    ])
  
def plot_model(model):
    X_plot = np.linspace(-3, 3, 100).reshape(100, 1)
    y_plot = model.predict(X_plot)

    plt.scatter(x, y)
    plt.plot(X_plot[:,0], y_plot, color='r')
    plt.axis([-3, 3, 0, 6])
    plt.show()


ridge1_reg = RidgeRegression(20, 0.0001)
ridge1_reg.fit(X_train, y_train)

y1_predict = ridge1_reg.predict(X_test)
print(mean_squared_error(y_test, y1_predict))

plot_model(ridge1_reg)
image-20251012185951012

可以发现α=0.0001\alpha=0.0001 相比原来直接多项式回归更加平滑，MSE=1.32MSE=1.32 比之前167好很多。同时观察随着α\alpha 增大为1，100，相应的MSEMSE 还在不断减少，同时曲线更加平滑，但到α=100\alpha=100 正则化有些过头了。而当α\alpha 无穷大时，可以发现均方误差变大了，近乎变成了一条直线。

可以发现岭回归引入了α\alpha 这个超参数

LASSO

LASSO全称为Least Absolute Shrinkage and Selection Operator Regression.

岭回归的目标是：

目标：使得J(θ)=MSE(y,y^;θ)+α12∑i=1nθi2尽可能小目标：使得J(\theta)=MSE(y,\hat{y};\theta)+\alpha\frac{1}{2}\sum_{i=1}^{n}\theta_i^2尽可能小

而LASSO Regression和岭回归Ridge Regression的原理是一样的，只不过在怎么表达θ\theta 最小上选用了一个不同的指标：

目标：使得J(θ)=MSE(y,y^;θ)+α∑i=1n∣θi∣尽可能小目标：使得J(\theta)=MSE(y,\hat{y};\theta)+\alpha\sum_{i=1}^{n}|\theta_i|尽可能小

可以发现两者区别主要在正则化项处，数学意义上都是让θi\theta_i 尽可能小，那么LASSO的具体效果如何呢？

编程实现：

  • 数据依然采用跟上面Ridge Regression中一样的种子：
1
2
3
4
5
6
7
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(42)
x = np.random.uniform(-3.0, 3.0, size=100)
X = x.reshape(-1, 1)
y = 0.5 * x + 3 + np.random.normal(0, 1, size=100)
  • 同时还是先采用degree=20的多项式回归，这前两步跟上面Ridge Regression完全一致
image-20251012232829340
  • Lasso回归，α\alpha 分别取0.01，0.1，1
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
from sklearn.linear_model import Lasso

def LassoRegression(degree, alpha):
    return Pipeline([
        ("poly", PolynomialFeatures(degree=degree)),
        ("std_scaler", StandardScaler()),
        ("lasso_reg", Lasso(alpha=alpha))
    ])
    
lasso1_reg = LassoRegression(20, 0.01)
lasso1_reg.fit(X_train, y_train)

y1_predict = lasso1_reg.predict(X_test)
print(mean_squared_error(y_test, y1_predict))

plot_model(lasso1_reg)

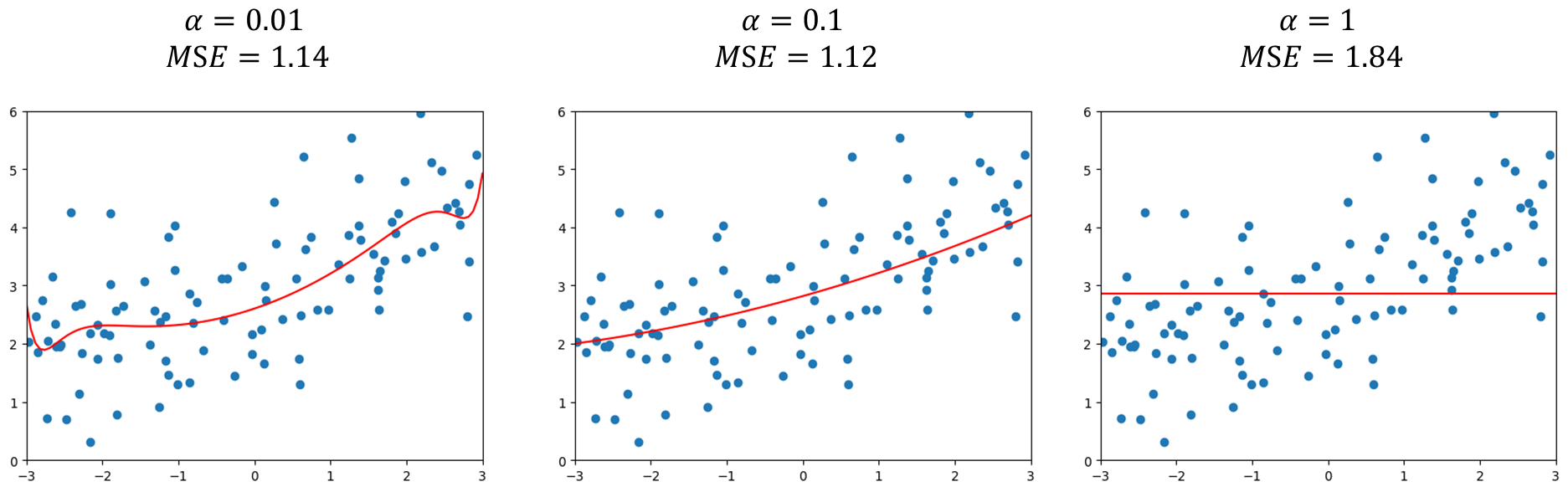
image-20251012233718152

先选取α=0.01\alpha=0.01 比Ridge Regression中大了很多，主要因为LASSO中正则项一次项，而Ridge是平方和需要更小的α\alpha ,当然具体还是需要实验调参。增大α=0.1\alpha=0.1 可以发现此时已经接近一条直线了，而α=1\alpha=1 可以发现基本是一条平行的直线，说明此时正则化程度非常高了。

当然实际中需要在完全不正则化的结果和这样正则化过头的结果之间选择一个程度最好的参数。同时可以发现Ridge中随着α\alpha 增大随然曲线更加平缓，但它始终是一个曲线，而LASSO在α=0.1\alpha=0.1 就已经近乎是一条直线了。LASSO趋向于使得一部分theta值为0，所以可作为特征选择用，也对应其名字中的Selection Operator Regression，但正因为这种特性LASSO可能会将一些原本有用的特征变为0，从计算准确度来将Ridge更准确。

L1,L2正则及弹性网络

无论是本次的Ridge和LASSO，还是回归算法评价标准中的MSE和MAE，以及欧拉距离和曼哈顿距离，它们整体形式基本是一样的。

image-20251013014132044

上面的形式本质上是一个LpLp范数：

∣∣X∣∣p=(∑i=1n∣xi∣p)1p||X||_p=(\sum_{i=1}^n|x_i|^p)^{\frac{1}{p}}

p=1p=1 是L1范数，p=2p=2 是L2范数。因此上面第一行都是L2正则，第二行都是L1正则。

弹性网Elasic Net:

J(θ)=MSE(y,y^;θ)+rα∑i=1n∣θi∣+1−r2α∑i=1nθi2J(\theta)=MSE(y,\hat y;\theta)+r\alpha\sum_{i=1}^n|\theta_i|+\frac{1-r}{2}\alpha\sum_{i=1}^{n}\theta_i^2

弹性网就是结合L1和L2正则的一种方式，只不过又引入一个超参数r，来表示两种正则的比例。

总结

机器学习主要解决的问题是过拟合问题，而我们训练模型不是为了拟合训练数据集，而是为了得到一个可以用到真实环境的泛化的模型。因此引入了Train-Test-Split通过测试集来测试模型泛化能力，但是同样有一个问题就是模型会针对特定测试数据集过拟合，因此我们引入验证数据集，但同样还有一个问题就是随机。因为每一次验证的数据集都是随机的从原来的数据切出来的，而训练的模型有可能过拟合验证数据集。由此我们引入了交叉验证来解决这个问题。接下来偏差和方差一个更高的角度来认识模型的误差，为了解决过拟合问题或者解决模型含有较大方差误差的问题，引入了正则化的概念，针对回归问题L1正则为LASSO回归，L2正则为Ridge Regression即岭回归。

这些概念方法自始至终围绕着模型泛化这个问题，即为了得到一个能应用到真实场景的模型，当然模型正则化手段远不止这些，道阻且长，一起学习进步哈哈~。