机器学习(9):逻辑回归

Logistic Regression

kaggle在2017年发布了一篇名为”The State of Data Science and Machine Learning “的报告，报告里面有这样一个问题：

What data science methods are used at work?

Logistic regression is the most commonly reported data science method used at work for all
industries except Military and Security where Neural Networks are used slightly more frequently.

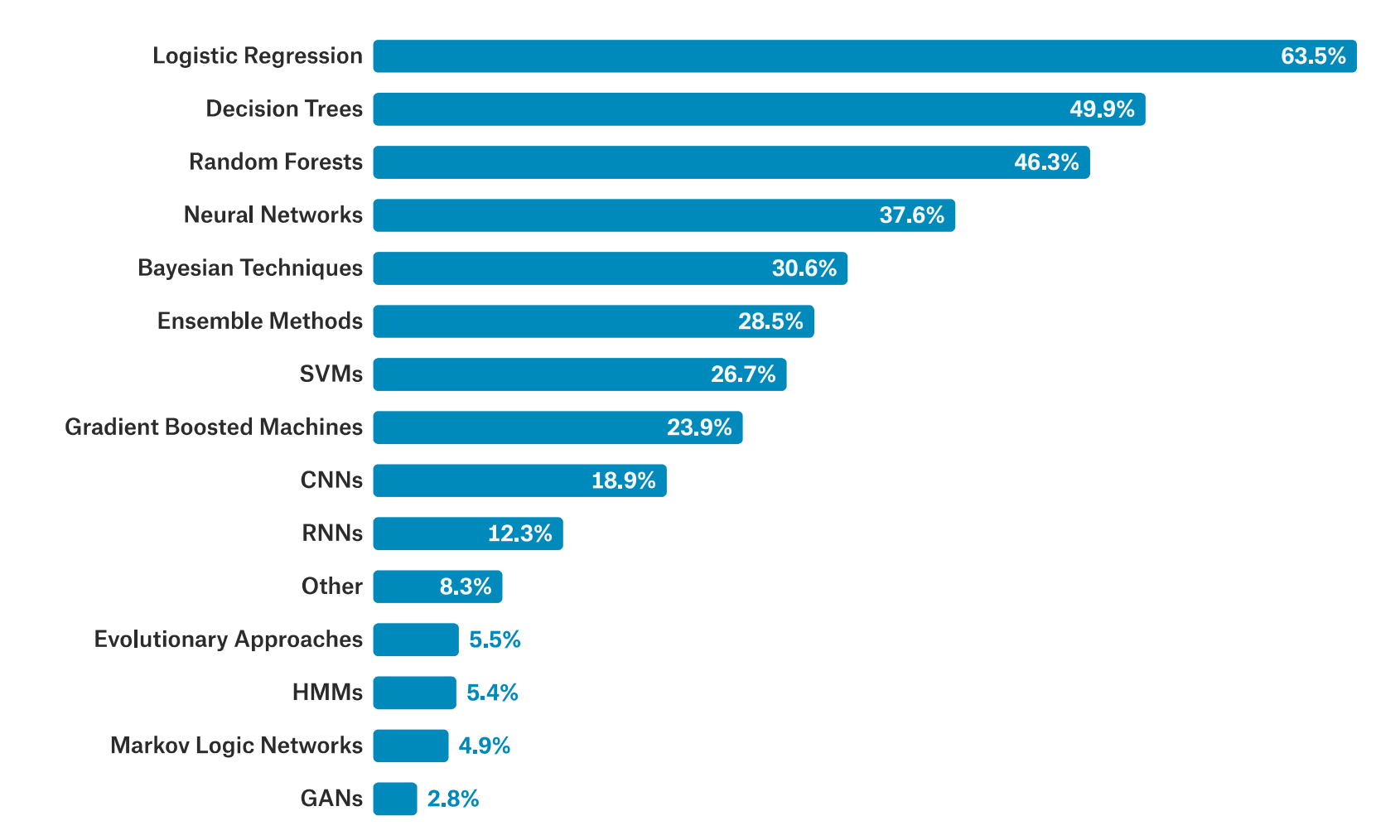
大意就是逻辑回归是各行业中工作中最常使用的数据科学方法，除了在军事和安全领域中，因为军事安全领域神经网络的使用频率略高一些。同时里面有这样一张图：

可以发现2017年之前逻辑回归、决策树、随机森林是当时使用率的前三名，相比而言CNN、RNN等深度学习方法排名相对靠后。逻辑回归算法思路比较简单，使用率排名第一，可见其非常有用。

什么是逻辑回归？

逻辑回归(Logistic Regression)从名字上看是一个回归算法，但其主要用来解决分类问题的。那么回归算法怎么解决分类问题呢？逻辑回归主要原理是将样本特征和样本发生的概率联系起来，即预测样本发生的概率是多少，概率是一个数，所以可以当作一个回归问题。

机器学习算法本质是求出一个函数$f$，传入一个样本$x$，然后得到预测值$\hat{y}$：
$$
\hat{y}=f(x)
$$
对于之前的线性回归、多线性回归等这个$\hat{y}$ 的值就是本身关心的指标比如预测房价、学生成绩等。但逻辑回归中我们得到的本质上是一个概率值：
$$
\hat{p}=f(x)\
\hat{y} =
\begin{cases}
1, & \hat{p} \ge 0.5 \
0, & \hat{p} < 0.5
\end{cases}
$$
根据概率值的大小我们进而可以进行分类，比如上面$\hat{p} \ge0.5$ 为1，$\hat{p} <0.5$ 为0。

逻辑回归既可以看做是回归算法，也可以看做是分类算法。通常作为分类算法用，只可以解决二分类问题。而KNN算法天生可以解决多分类问题，逻辑回归需要一些其他技巧改进才可以解决多分类问题。

那么逻辑回归通过什么样的方式来得到一个事件的概率值？线性回归中：
$$
\hat{y}=\theta^T.x_b \quad 值域(-inf,+inf)\
概率的值域[0,1]
$$
如果直接用$\hat {y}$ 的值表示事件概率，从应用角度可以这样做，但因为概率有值域的限制，这样结果可信度很差。因此解决方案很简单，将回归结果在送给一个$\sigma$ 函数:
$$
\hat{p}=\sigma(\theta^T.x_b)
$$
此时值域就变为了[0,1]之间，但这个$\sigma$ 函数是什么？

$\sigma$ 也叫做Sigmoid函数，表达式：
$$
\sigma(t)=\frac{1}{1+e^{-t}}
$$

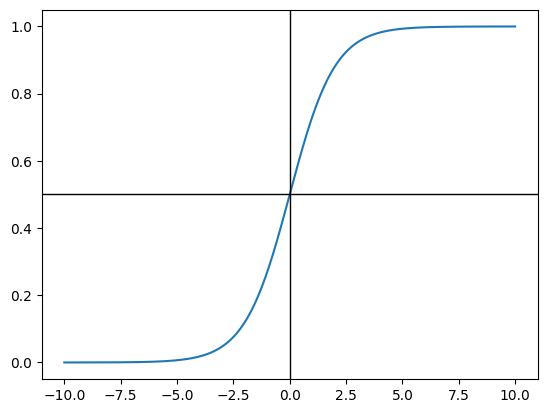
import numpy as np
import matplotlib.pyplot as plt

def sigmoid(t):
    return 1 / (1 + np.exp(-t))
 
x = np.linspace(-10, 10, 500)
y = sigmoid(x)

plt.plot(x, y)
plt.axhline(0.5, color='black', linewidth=1) 
plt.axvline(0, color='black', linewidth=1)  
plt.show()

可以发现Sigmoid函数值域就在[0,1]之间，当$t>0$时$p>0.5$ ,当$t<0$时$p<0.5$ ,当$t=0$时$p=0.5$

所以整体上逻辑回归的表达式：
$$
\hat{p}=\sigma(\theta^T.x_b)=\frac{1}{1+e^{-\theta^T.x_b}}\
\hat{y}=
\begin{cases}
1, & \hat{p} \ge 0.5\
0, & \hat{p} \le 0.5
\end{cases}
$$
那么剩下的问题就是：对于给定的样本数据集X,y,我们如何找到参数theta,使得用这样的方式可以最大程度获得样本X对应的分类输出y?

逻辑回归的损失函数

回想线性回归中是通过$y-\hat{y}$ 的差来度量模型估计的好坏，在进行变形以MSE作为损失函数，然后找到让损失函数最小的$\theta$ 值就好了. 同理逻辑回归也应该这样做，只不过问题在于损失函数该如何定义？

首先逻辑回归跟前面线性回归最大的一个区别是逻辑回归解决的是分类问题，我们要根据估计出来的$\hat{p}$ 来决定最后的$\hat{y}$ 是1还是0，因此损失函数也可以分为两类:
$$
cost=
\begin{cases}
如果y=1,p越小,cost越大\
如果y=0,p越大,cost越大\
\end{cases}\
\downarrow\
cost=
\begin{cases}
-log(\hat{p})\quad if \quad y=1 \
-log(1-\hat{p})\quad if \quad y=0\
\end{cases}\
$$
如何理解呢？这里的$y$ 是真值，比如$y=1$ ，如果此时估计的$p$ 越小，那么我们越倾向将$\hat{y}$ 估计为0，即估计错误，这种情况损失应该越大；同理$y=0$ ，如果此时估计的$p$ 越大，那么我们越倾向将$\hat{y}$ 估计为1，即估计错误，这种情况损失也应该越大。

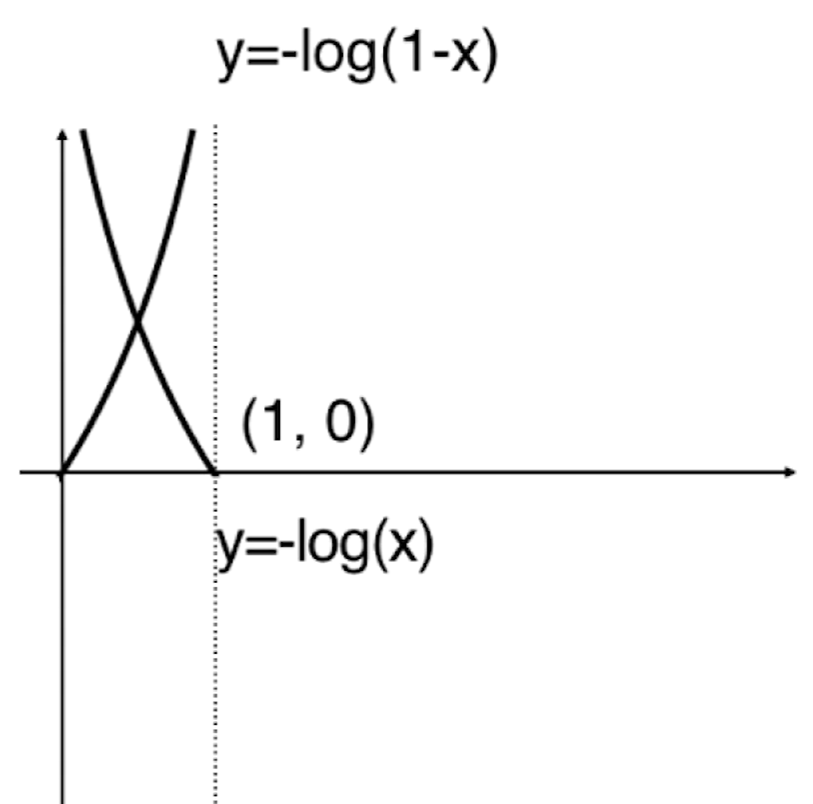
绘制出两个函数图像：

此时无论$y=1$ 还是$y=0$ ，都满足上面说的情况，比如看$y=-log(x)$ ，$x$ 越小，相应损失就越大。对于$y=-log(1-x)$ 反之。

但此时的惩罚函数整体是一个分类函数，需要依据$y$ 的取值0，1来选择不同的函数，显然很不方便，因此可以通过一个很简单的手段进行合成：
$$
cost=-ylog(\hat{p})-(1-y)log(1-\hat{p})
$$
显然当$y=1$时$cost=-ylog(\hat p)$ ,$y=0$ 时$cost=-(1-y)log(1-\hat{p})$ .

上面是一个样本的情况，对于m个样本就是：
$$
J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log(\hat{p}^{(i)})+(1-y^{(i)})log(1-\hat{p}^{(i)})\
\hat{p}^{(i)}=\sigma(X^{(i)}_b\theta)=\frac{1}{1+e^{-X_b^{(i)}\theta}}
$$
到此，我们的目标就是找到一组$\theta$ 使得$J(\theta)$ 最小。同时对于这个$J(\theta)$ 式子不能像线性回归损失函数一样推导出一个正规方程解，这个式子没有数学解析解的，所以只能使用梯度下降法求解。

逻辑回归损失函数梯度推导

观察到$J(\theta)$ 种含有$\sigma$ 函数，因此先尝试对$\sigma$ 求导:
$$
\sigma(t)=\frac{1}{1+e^{-t}}=(1+e^{-t})^{-1}\
\sigma(t)^{,}=-(1+e^{-t})^{-2}.(-e^{-t})=(1+e^{-t})^{-2}.e^{-t}
$$
在此基础上对$log\sigma(t)$ 求导:
$$
(log\sigma(t))^,=\frac{\sigma(t)^,}{\sigma(t)}=\frac{1}{\sigma(t)}.(1+e^{-t})^{-2}.e^{-t}\
=\frac{1}{(1+e^{-t})^{-1}}.(1+e^{-t})^{-2}.e^{-t}\
=(1+e^{-t})^{-1}.e^{-t}\
=\frac{e^{-t}}{1+e^{-t}}=1-\frac{1}{1+e^{-t}}\
=1-\sigma(t)
$$
同理看一下$log(1-\sigma(t))$ 的导数：
$$
(log(1-\sigma(t)))^,=\frac{-\sigma(t)^,}{1-\sigma(t)}=\frac{-(1+e^{-t})^{-2}.e^{-t}}{1-\sigma(t)}\
=\frac{-(1+e^{-t})^{-2}.e^{-t}}{1-(1+e^{-t})^{-1}}\
=\frac{-(1+e^{-t})^{-1}.e^{-t}}{1+e^{-t}-1}\
=-(1+e^{-t})^{-1}\
=-\sigma(t)
$$
因此可得到$J(\theta)$ 对一个$\theta_j$ 的导数：
$$
J(\theta)=-\frac{1}{m}\sum_{i=1}^{m}y^{(i)}log(\hat{p}^{(i)})+(1-y^{(i)})log(1-\hat{p}^{(i)})\
\frac{d(y^{(i)}log(\sigma(X_b^{(i)}\theta)))}{d\theta_j}=y^{(i)}(1-\sigma(X_b^{(i)}\theta)).X_j^{(i)}\
\frac{d((1-y^{(i)})log(1-\sigma(X_b^{(i)}\theta)))}{d\theta_j}=(1-y^{(i)})(-\sigma(X_b^{(i)}\theta)).X_j^{(i)}\
\frac{J(\theta)}{\theta_j}=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}(1-\sigma(X_b^{(i)}\theta)).X_j^{(i)}+(1-y^{(i)})(-\sigma(X_b^{(i)}\theta)).X_j^{(i)})\=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}.X_j^{(i)}-y^{(i)}\sigma(X_b^{(i)}\theta).X_j^{(i)}-\sigma(X_b^{(i)}\theta).X_j^{(i)}+y^{(i)}\sigma(X_b^{(i)}\theta).X_j^{(i)})\
=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}.X_j^{(i)}-\sigma(X_b^{(i)}\theta).X_j^{(i)})\
=-\frac{1}{m}\sum_{i=1}^{m}(y^{(i)}-\sigma(X_b^{(i)}\theta)).X_j^{(i)}\
=\frac{1}{m}\sum_{i=1}^{m}(\sigma(X_b^{(i)}\theta)-y^{(i)}).X_j^{(i)}\
=\frac{1}{m}\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_j^{(i)}
$$
进而逻辑回归损失函数梯度表达式：
$$
\triangledown J(\theta)=\begin{pmatrix}
\frac{\partial J}{\partial w_0} \
\frac{\partial J}{\partial w_1} \
…\
\frac{\partial J}{\partial w_n}
\end{pmatrix}
= \frac{1}{m}
\begin{pmatrix}
\sum_{i=1}^{m}(\sigma(X_b^{(i)}\theta)-y^{(i)}).1 \
\sum_{i=1}^{m}(\sigma(X_b^{(i)}\theta)-y^{(i)}).X_1^{(i)} \
…\
\sum_{i=1}^{m}(\sigma(X_b^{(i)}\theta)-y^{(i)}).X_n^{(i)}
\end {pmatrix}\
= \frac{1}{m}
\begin{pmatrix}
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).1 \
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_1^{(i)} \
…\
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_n^{(i)}
\end {pmatrix}\
$$
在这里顺便回想一下线性回归的梯度表达式：

可以发现两者区别在于线性回归是$X_b^{(i)}\theta$ , 而逻辑回归是$\sigma(X_b^{i}\theta)$ ,但里面都是$\hat{y}^{(i)}-y^{(i)}$。

向量化

对上面推导出的逻辑回归梯度表达式进行向量化：
$$
\triangledown J(\theta)=
= \frac{1}{m}
\begin{pmatrix}
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).1 \
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_1^{(i)} \
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_2^{(i)} \
…\
\sum_{i=1}^{m}(\hat{y}^{(i)}-y^{(i)}).X_n^{(i)}
\end {pmatrix}
=\frac{1}{m}.X_b^T.(\sigma(X_b\theta)-y)
$$

逻辑回归实现

根据上面的思路编写LogisticRegression类:

import numpy as np
from .metrics import accuracy_score


class LogisticRegression:

    def __init__(self):
        self.coef_ = None
        self.interception_ = None
        self._theta = None
    
    def _sigmoid(self, t):
        return 1. / (1. + np.exp(-t))
    
    def fit(self, X_train, y_train, eta=0.01, n_iters=1e4):
        assert X_train.shape[0] == y_train.shape[0],\
        "the size of X_train must be equal to the size of y_train"

        def J(theta, X_b, y):
            y_hat = self._sigmoid(X_b.dot(theta))
            try:
                return np.sum(y*np.log(y_hat) + (1-y)*np.log(1-y_hat))/len(X_b)
            except:
                return float('inf')
            
        def dJ(theta, X_b, y):

            return X_b.T.dot(self._sigmoid(X_b.dot(theta))-y)/len(y)
            
        def gradient_descent(X_b, y , initial_theta, eta, n_iters=1e4, eps=1e-8):

            theta = initial_theta
            i_iter = 0
            while i_iter < n_iters:
                gradient = dJ(theta, X_b, y)
                last_theta = theta
                theta = theta - eta*gradient

                if abs(J(theta, X_b, y)-J(last_theta,X_b,y)) <eps:
                    break
                i_iter +=1
            return theta

        X_b = np.hstack([np.ones((len(X_train),1)),X_train])
        initial_theta = np.zeros(X_b.shape[1])

        self._theta = gradient_descent(X_b, y_train , initial_theta, eta, n_iters=1e4)
        self.interception_ = self._theta[0]
        self.coef_ = self._theta[1:]

        return self

    def predict(self, X_predict):
        assert self.coef_ is not None and self.interception_ is not None,\
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_),\
            "the feature number of X_predict must be equal to X_train"
        proba = self.predict_proba(X_predict)

        return np.array(proba >= 0.5, dtype='int')

    def predict_proba(self, X_predict):
        assert self.coef_ is not None and self.interception_ is not None,\
            "must fit before predict!"
        assert X_predict.shape[1] == len(self.coef_),\
            "the feature number of X_predict must be equal to X_train"
        X_b = np.hstack([np.ones((len(X_predict),1)),X_predict])

        return self._sigmoid(X_b.dot(self._theta))  
     
    def score(self, X_test,y_test):
        y_predcit = self.predict(X_test)
        return accuracy_score(y_test, y_predcit)
    
    def __repr__(self):
        return "LogisticRegression()"

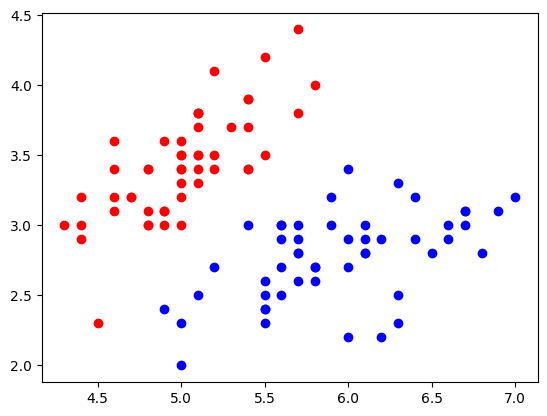
接下来在scikit-learn中的鸢尾花iris数据上试用，考虑到iris数据集一共有四类，而LogisticRegerssion只能解决二分类问题，这里对iris数据集进行一个简单的处理，只保留前两类,同时为例方便可视化只取前两列特征：

import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data
y = iris.target

X = X[y<2, :2]
y = y[y<2]

plt.scatter(X[y==0, 0], X[y==0, 1], c='r')
plt.scatter(X[y==1, 0], X[y==1, 1], c='b')
plt.show()

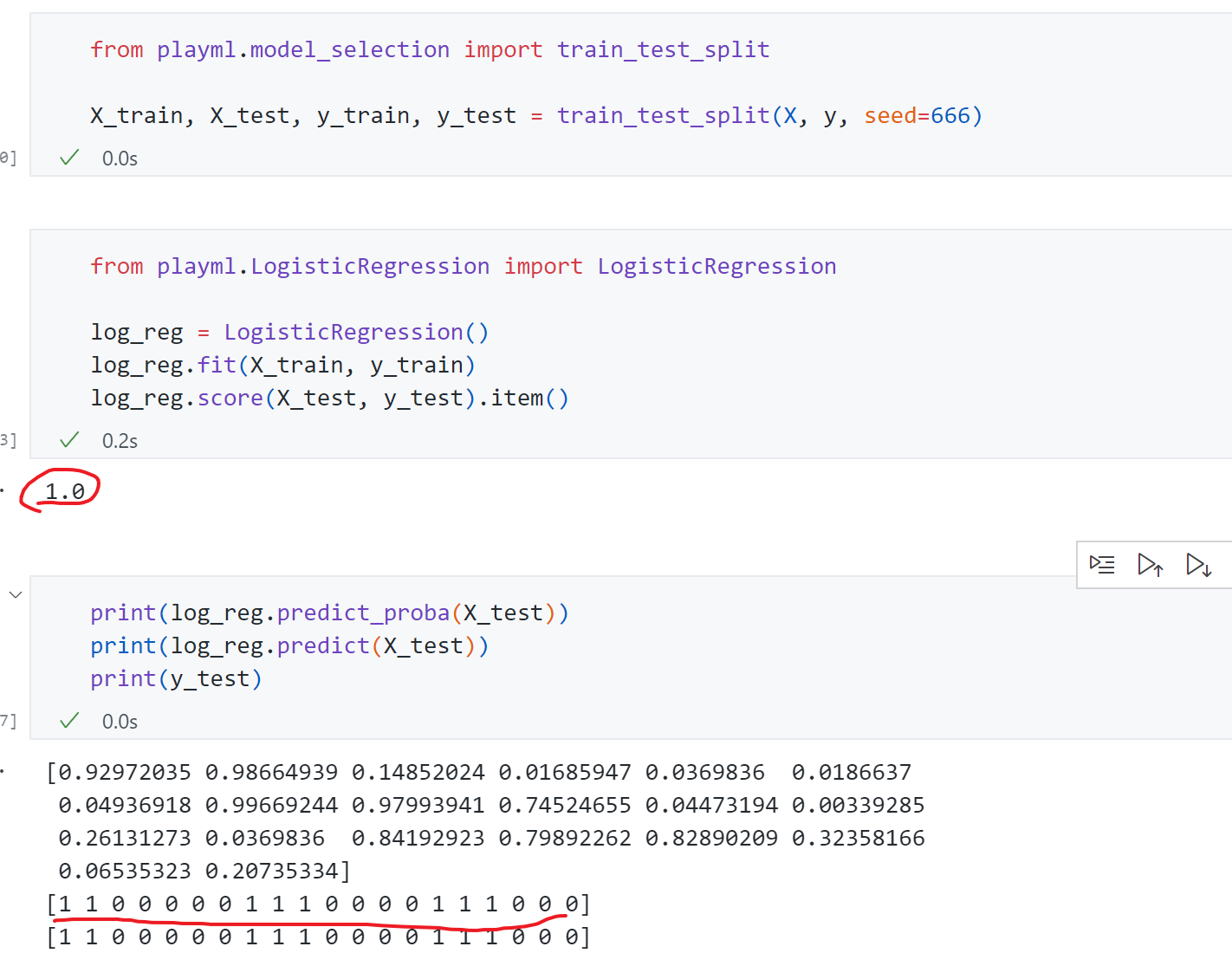
然后训练测试：

测试准确为100%，打印出来可以发先概率以及对应预测的标签，真实标签越接近1的概率越大，真实标签越接近0的概率越小。准确率能100%主要因为iris数据过于简单，同时我们只取了两个特征比较好分类。

决策边界

逻辑回归同样也能求出coef和intercept,那它的几何意义是什么，如何看待这些参数值呢？这就涉及到分类问题一个很重要的概念-决策边界。

回顾逻辑回归的表达式：
$$
\hat{p}=\sigma(\theta^T.x_b)=\frac{1}{1+e^{-\theta^T.x_b}}\
\hat{y}=
\begin{cases}
1, & \hat{p} \ge 0.5 & \theta^T.x_ \ge0\
0, & \hat{p} \le 0.5 & \theta^T.x_ <0
\end{cases}
$$
决策边界为$\theta^T.x_b=0$.

如果X有两个特征，则$\theta_0+\theta_1x_1+\theta_2x_2=0$,此时其代表一条直线：
$$
x_2=\frac{-\theta_0-\theta_1x_1}{\theta_2}
$$
因此绘制一下这个决策边界：

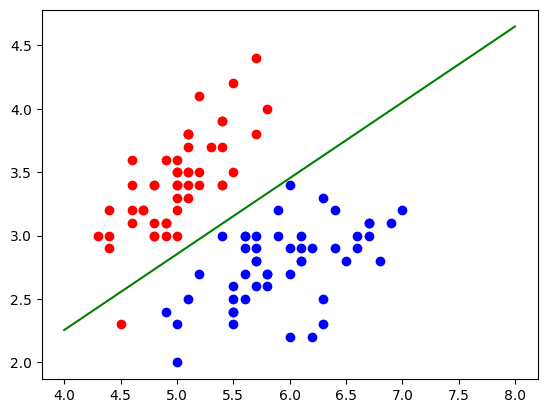
def x2(x1):
    return (-log_reg.coef_[0]*x1 - log_reg.interception_ )  / log_reg.coef_[1]

x1_plot = np.linspace(4, 8, 1000)
x2_plot = x2(x1_plot)

plt.scatter(X[y==0,0], X[y==0,1], color="red")
plt.scatter(X[y==1,0], X[y==1,1], color="blue")
plt.plot(x1_plot, x2_plot, c='g')
plt.show()

绿线即为决策边界，>0则分类为1即下方的点，<0上方的点分类为0.同时可以发现有个红色点分类错误，但是前面测试集准确率100%，说明这个点在训练集中。

通过上图可以发现，对于逻辑回归算法来说其决策边界是一条直线，但其实不论对于KNN，还是逻辑回归，可以加上多项式项使得决策边界不再是一条直线，此时需要一种不规则决策边界的绘制方法。

可以把特征平面看成无数的点，对每一个点都用模型来将其分类，这个过程以此类推对足够密的点继续分类并将颜色绘制出来，就得到了不规则的决策边界。

示例：

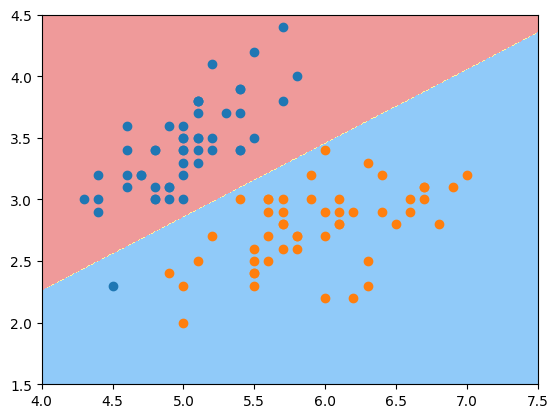
def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
    
plot_decision_boundary(log_reg, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

同理看一下KNN算法的决策边界，虽然KNN不像逻辑回归有决策边界的表达式，但依然可以通过上面提到的方式绘制出来：

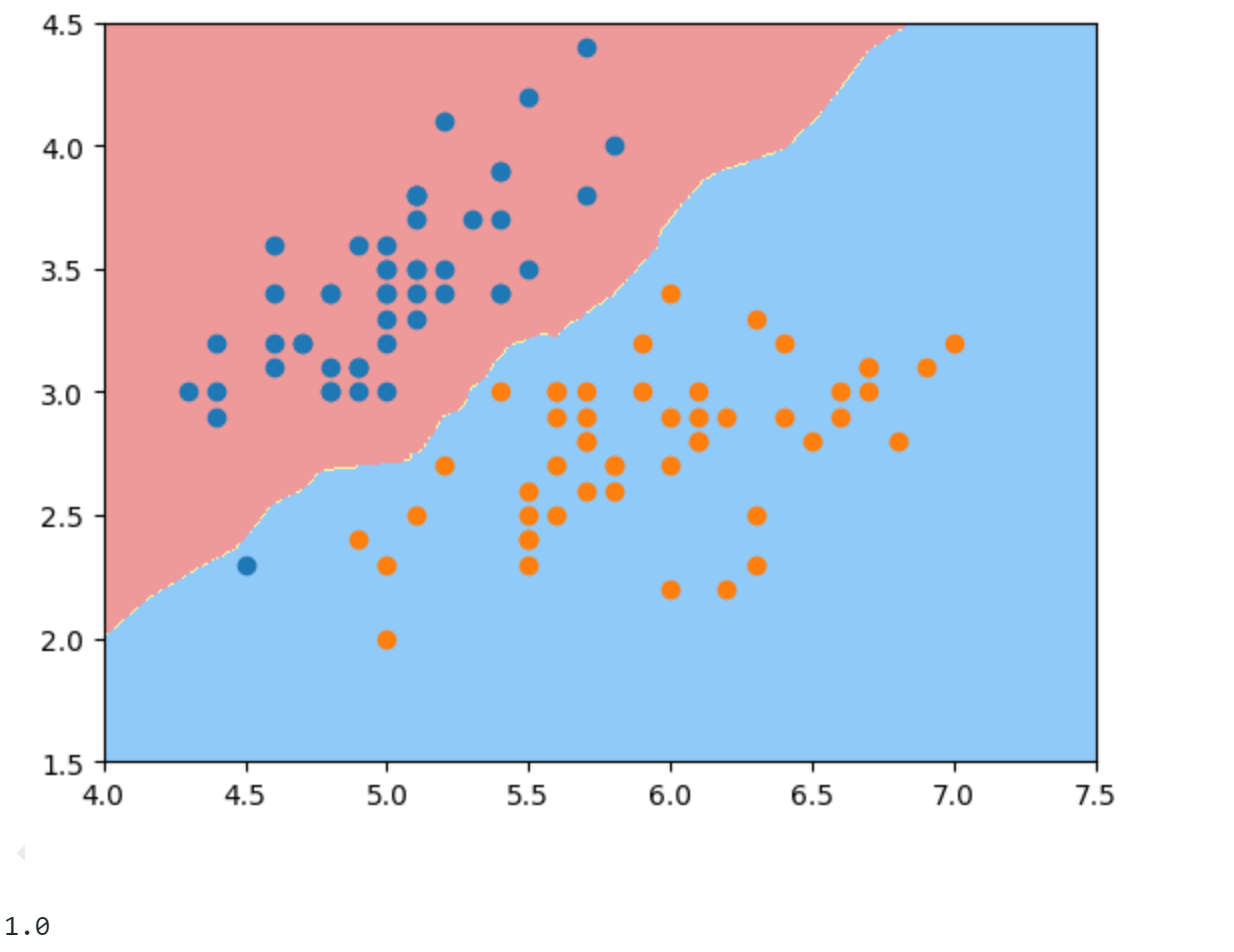
from sklearn.neighbors import KNeighborsClassifier

knn_clf  = KNeighborsClassifier()
knn_clf.fit(X_train, y_train)
print(knn_clf.score(X_test, y_test))

plot_decision_boundary(knn_clf, axis=[4, 7.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

可以发现KNN分类准确率也为100%，边界画出来是一条弯曲的曲线。

因为KNN可以解决多分类问题，所以尝试对iris三个类别进行分类可视化：

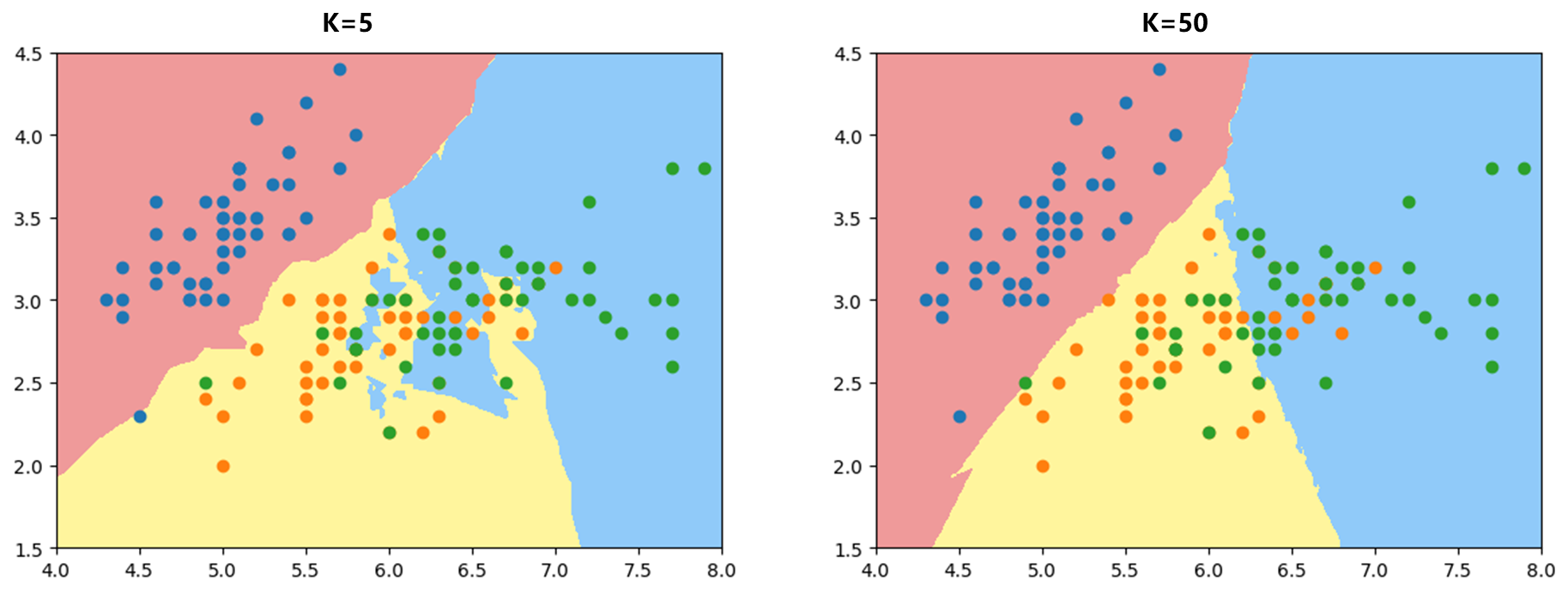
knn_clf_all = KNeighborsClassifier()
knn_clf_all.fit(iris.data[:,:2], iris.target)

plot_decision_boundary(knn_clf_all, axis=[4, 8, 1.5, 4.5])
plt.scatter(iris.data[iris.target==0,0], iris.data[iris.target==0,1])
plt.scatter(iris.data[iris.target==1,0], iris.data[iris.target==1,1])
plt.scatter(iris.data[iris.target==2,0], iris.data[iris.target==2,1])

可以发现$k=5$ 是决策边界不规则，明显过拟合，说明KNN算法k越小模型越复杂，而$k=50$是明显决策边界规整了很多，模型更简单。

多项式特征的逻辑回归

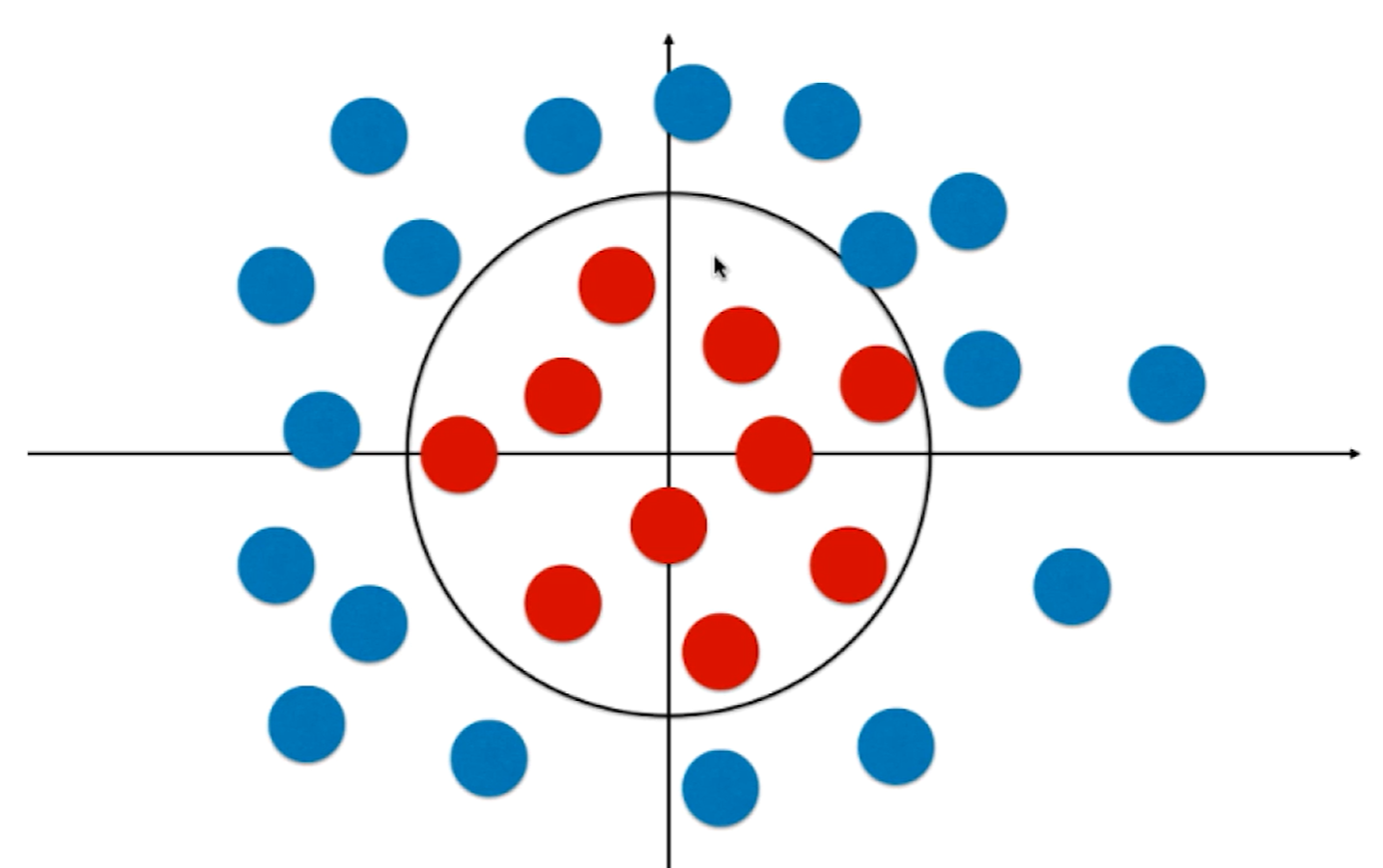
逻辑回归本质上在特征平面中找到一条直线分割样本两个分类，因此只可以解决二分类问题。但是实际问题中决策边界是大概率不规则的比如下面的圆形：

此时要找的边界应满足圆的方程： $x_1^2+x_2^2=r^2$ ，那么如何让逻辑回归学习到这样的决策边界？其实就是前面提到的多项式回归思路，引入多项式项即可。

通过多项式的组合构建几乎可以得到任意形状的决策边界。

编程示例：

随机生成样本数据

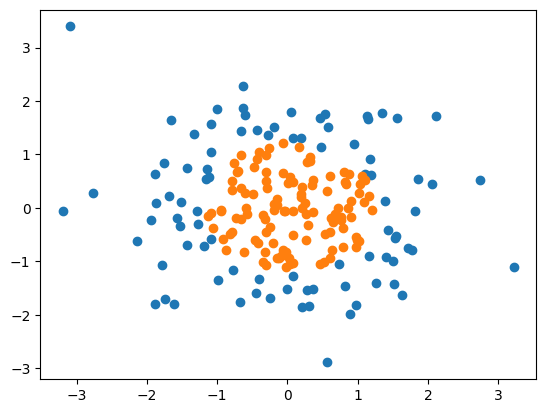
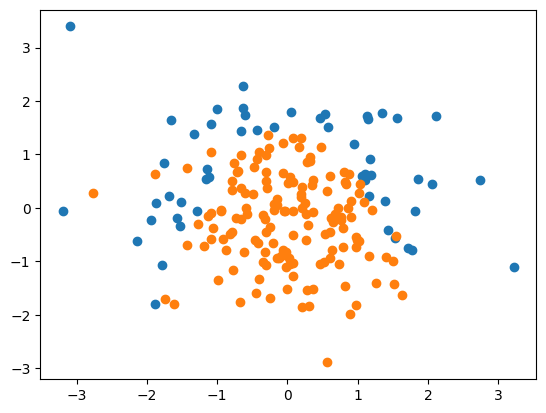
import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
X = np.random.normal(0, 1, size=(200,2))
y = np.array(X[:,0]**2 + X[:,1]**2 <1.5,dtype='int')

plt.scatter(X[y==0,0],X[y==0,1])
plt.scatter(X[y==1,0],X[y==1,1])
plt.show()

首先使用不加多项式特征的逻辑回归（代码同上面，只是数据改下）

准确率只有60.5%，可以发现决策边界是一条直线，有许多错误分类。

添加多项式特征

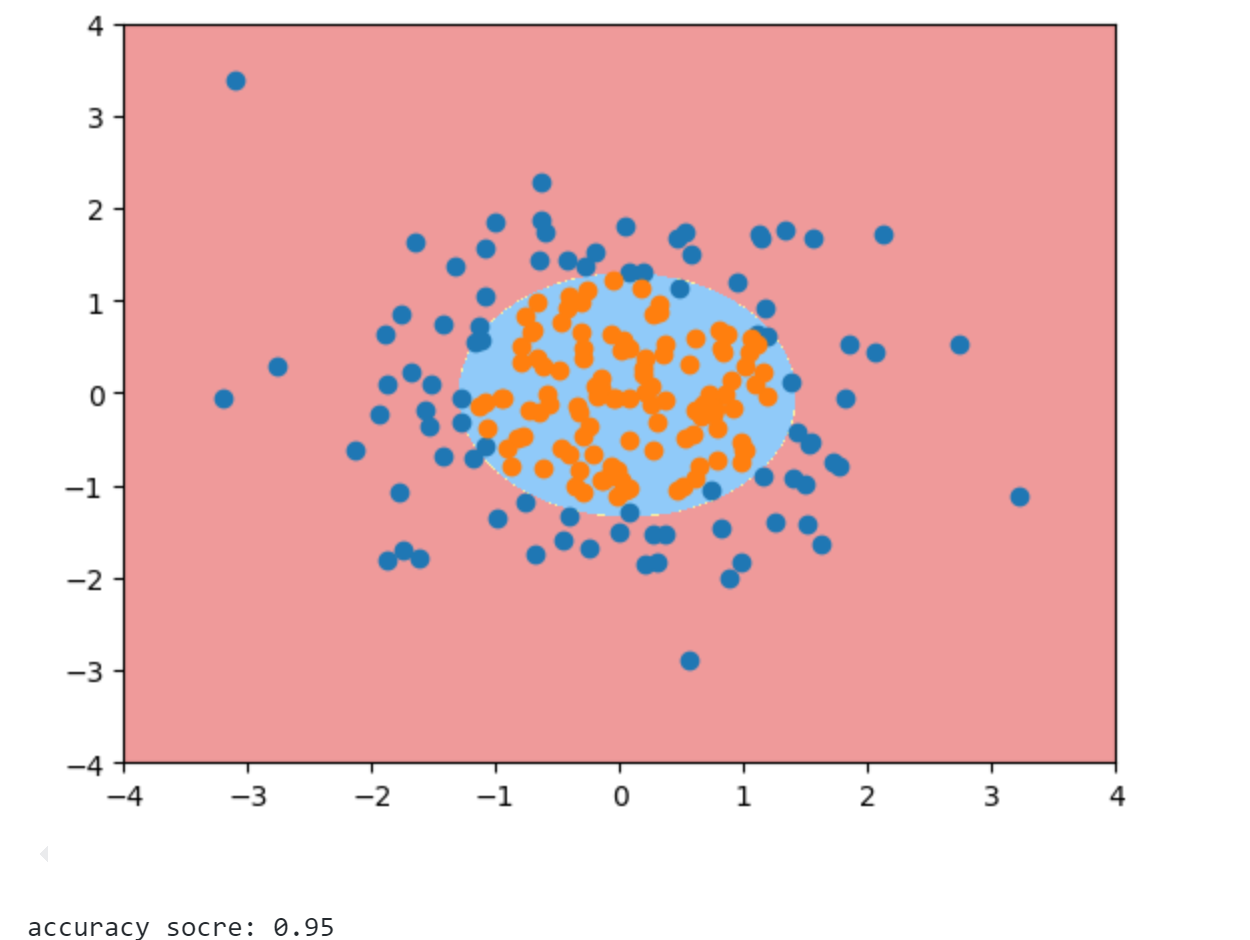
from sklearn.preprocessing import PolynomialFeatures
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler

def PolynomialLogisticRegression(degree):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression())
    ])
poly_log_reg = PolynomialLogisticRegression(degree=2)
poly_log_reg.fit(X, y)

print("accuracy socre:",poly_log_reg.score(X, y))
plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

此时准确率有95%，可以发现决策边界是一个圆形，对两类数据进行了很好的划分。

同时注意这里传入的LogisticRegression() 是前面自己定义的类，而不是skleran实现的，但仍能传进去，说明只要遵循sklearn的标注，有fit,predict，score等可以进行无缝衔接。

正则化

逻辑回归既然也可以添加多项式项来生成不规则的决策边界进而对非线性数据进行分类，但引入多项式项模型相应就会变的非常复杂造成过拟合，因此为了解决这个问题同样也要正则化。

前面将多项式回归的正则化方式是给损失函数添加一个L1或L2正则项：
$$
J(\theta)+\alpha L_1\
J(\theta)+\alpha L_2\
$$
Scikit-learn中的正则化方式：
$$
C.J(\theta)+L_1\
C.J(\theta)+L_2
$$
超参数C放在了损失函数面前，使用这种方式就不得不正则化，因为L1和L2前面系数至少是1.

scikit-learn中的逻辑回归自动封装了模型正则化项，只需要调整超参数C和正则化方式即可。

因此接下来看下Scikit-learn中的逻辑回归：

随机生成样本数据

import numpy as np
import matplotlib.pyplot as plt

np.random.seed(666)
X = np.random.normal(0, 1, size=(200, 2))
y = np.array((X[:,0]**2+X[:,1])<1.5, dtype='int')
for _ in range(20):
    y[np.random.randint(200)] = 1
    
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()

要注意一下这里构造y时使用的是抛物线($x_0^2+x_1$)的形式：

1
2
3

y = np.array((X[:,0]**2+X[:,1])<1.5, dtype='int')
for _ in range(20):
    y[np.random.randint(200)] = 1

因为牵扯到正则化，所以上面代码里随机选取了20个点强制其标签为1来添加噪声。

使用scikit-learn的逻辑回归

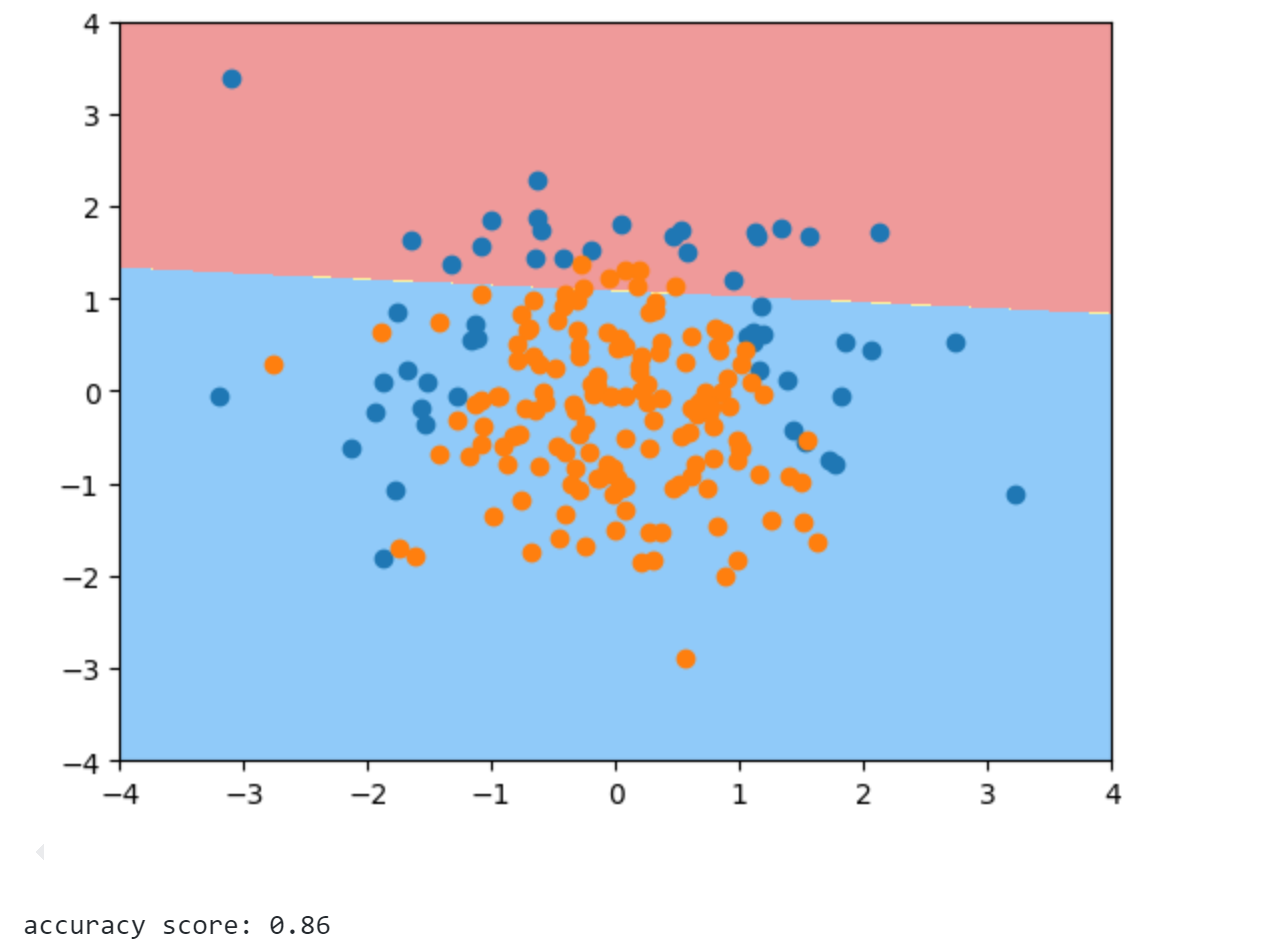
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.show()
print("accuracy score:",log_reg.score(X_test, y_test))

测试集准确率为86%，同时可以发现决策边界是一条直线。

加入多项式特征的逻辑回归

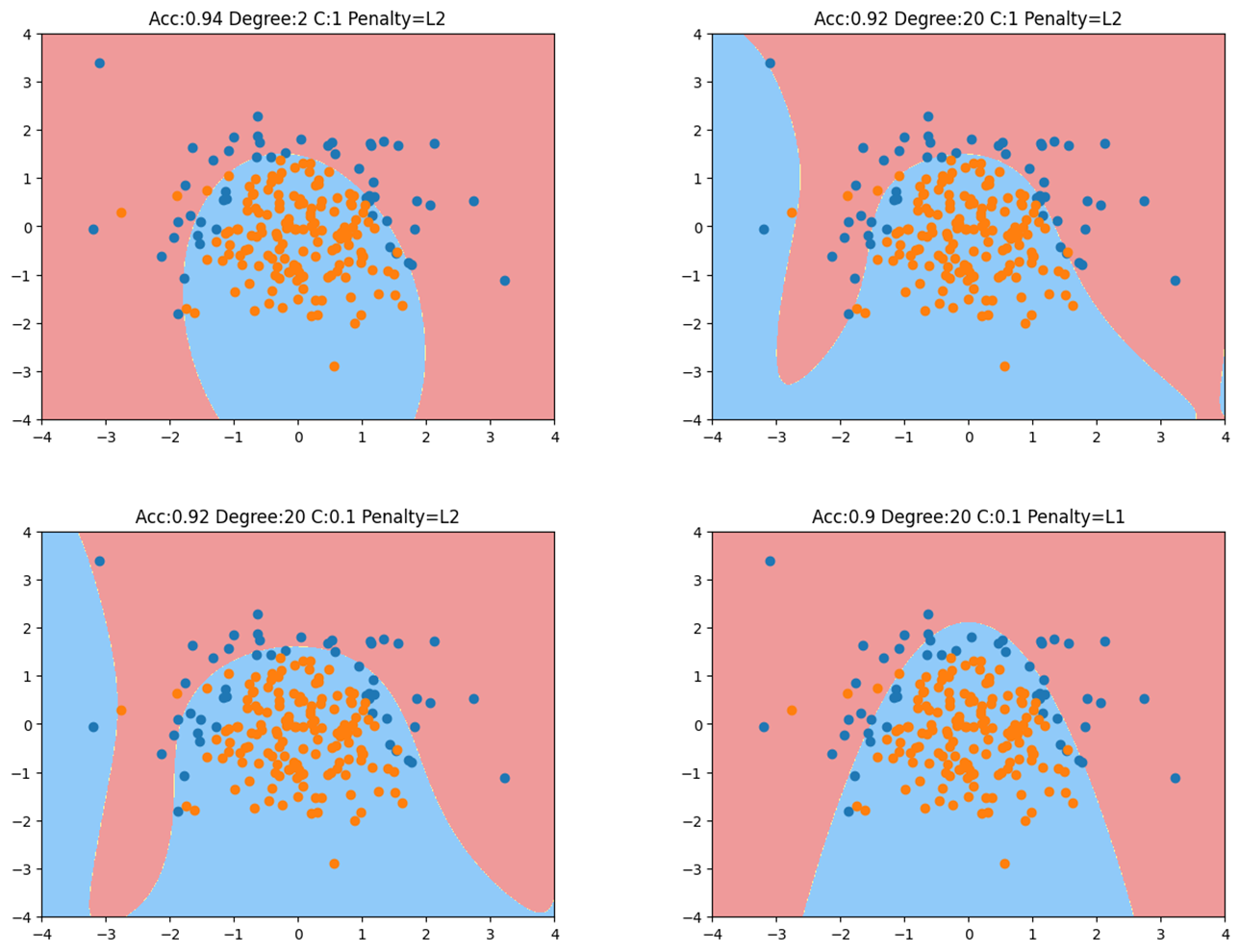
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import PolynomialFeatures
from sklearn.preprocessing import StandardScaler

def PolynomialLogisticRegression(degree, C, penalty='l2'):
    return Pipeline([
        ('poly', PolynomialFeatures(degree=degree)),
        ('std_scaler', StandardScaler()),
        ('log_reg', LogisticRegression(C=C, penalty=penalty,solver='liblinear'))
    ])

poly_log_reg = PolynomialLogisticRegression(degree=20, C=0.1, penalty='l2')
poly_log_reg.fit(X_train, y_train)


plot_decision_boundary(poly_log_reg, axis=[-4, 4, -4, 4])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.title(f"Acc:{poly_log_reg.score(X_test, y_test)} Degree:20 C:0.1 Penalty=L1")
plt.show()

$degree=2,C=1$ 时模型预测准确率为94%，并且决策边界是一个二次曲线。

$degree=20,C=1$ 时模型预测准确率为92%，决策边界明显不规则，说明此时可能过拟合。

$degree=20,C=0.1$ 时模型预测准确率为92%，此时C变小正则化项应该起更大作用，可以发现测试决策边界变好了一些。

$degree=20,C=0.1，L1正则$ 时模型预测准确率为90%，此时L1正则，决策边界已经非常接近我们生成数据时的形状了，说明L1正则能够使得$degree=20$中非常多的多项式项系数为0，使得决策边界不会像L2那样弯曲。

OvR与OvO

逻辑回归只能解决二分类问题，如何改造才能解决多分类问题呢？一般改造方式有两种OvR和OvO,这两种改造方式对几乎所有二分类算法都适用。

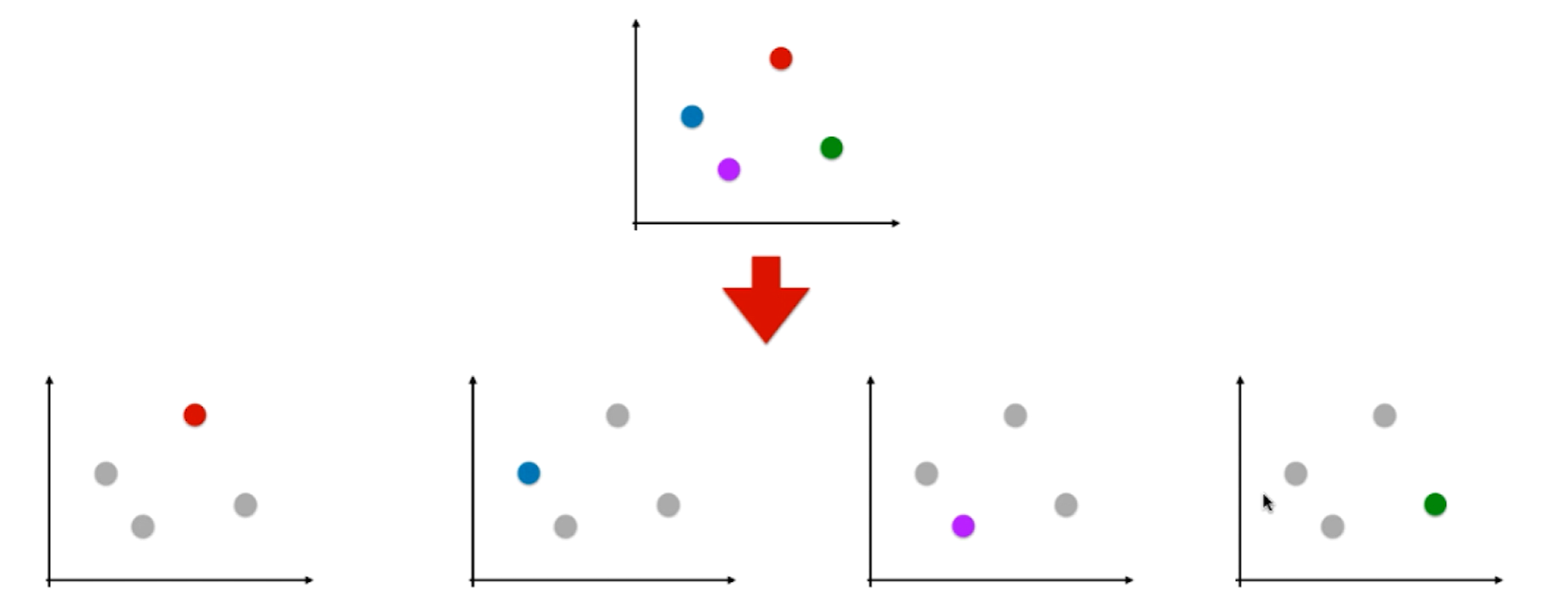
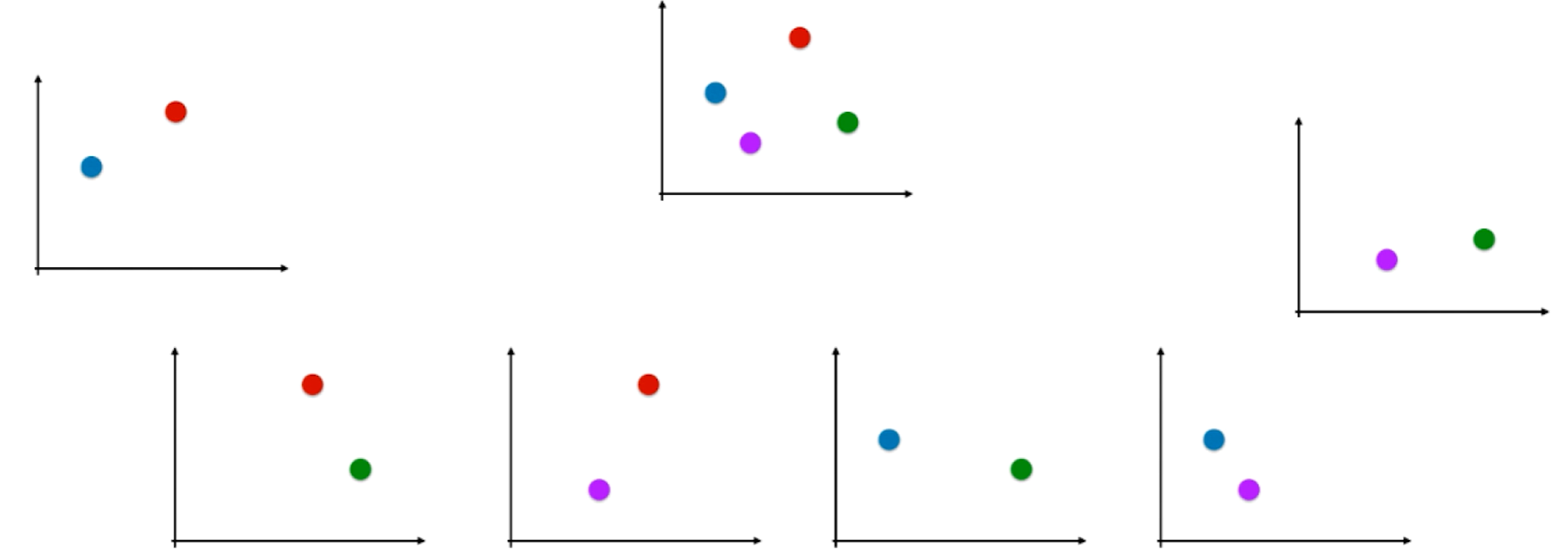
OvR即One vs Rest:

如上图假设有四个类别，我们将红色类别看为一类，剩下的蓝紫绿看为其他类别，此时四分类问题就转变为了二分类问题，此时就可以使用逻辑回归算法。同理就可以一共形成四个分类问题，每一个都是一种颜色和其余颜色的和进行分类。如果有n个类别就进行n次分类，选择分类得分最高的。缺点就是时间复杂度变高了。

OvR即One vs One:

如上图每次只针对两个类别进行分类，一共有$C_4^2=6$ 对，形成了6个二分类问题。针对每个二分类问题，都可以预测一下样本点处于当前二分类问题的哪个类别，然后对分类结果进行投票，看在哪个类别数量最大。因此如果有n各类别，就进行$C_n^2$ 次分类，选择赢数最高的分类。

显然OVO的方式的时间复杂度是$n^2$ 级别的，而OvR是n级别的。但是OVO这种方式分类结果更加准确，因为每次只用真实的两个类别比较而没有混淆其它的类别信息，所以更倾向得到新来样本真实的属于哪一个类别。

以iris鸢尾花数据集进行示例：

OvR方式和OvO方式（为了便于可视化先只用到数据的前2个特征）

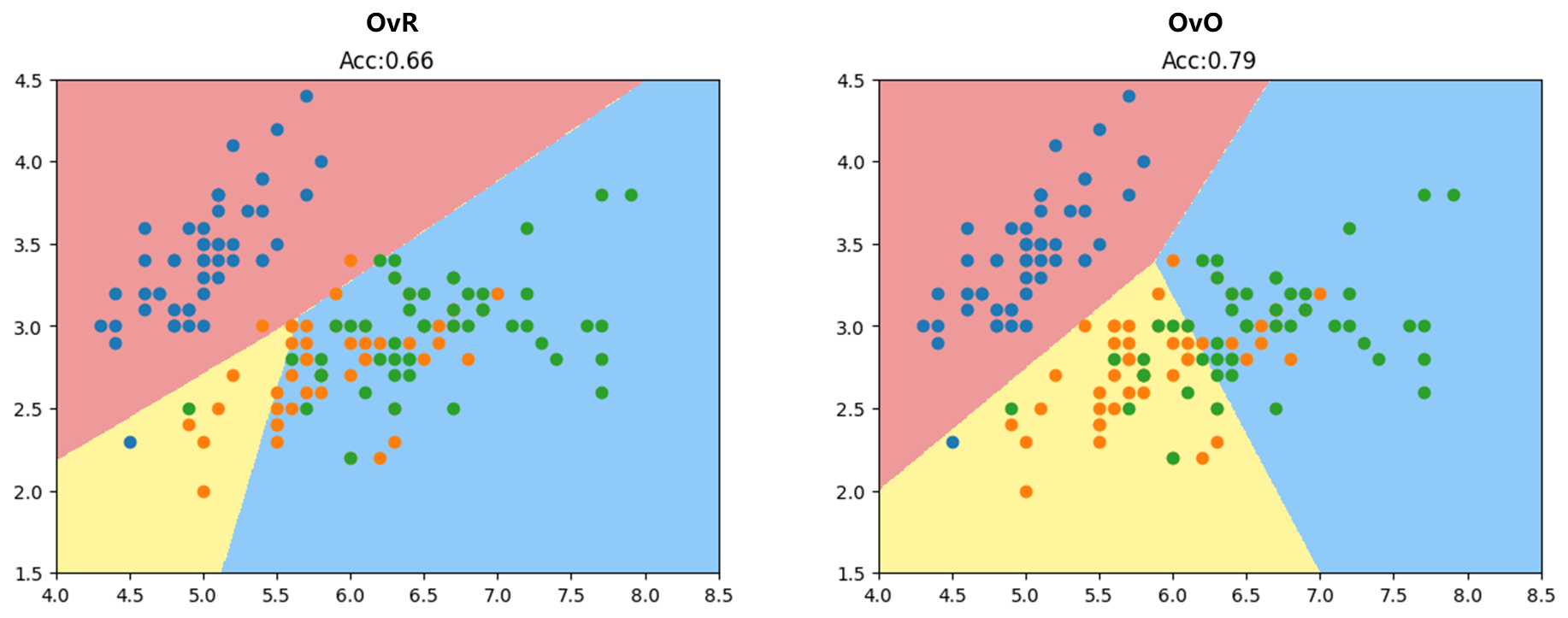
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

iris = datasets.load_iris()
X = iris.data[:,:2]
y = iris.target

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression(multi_class="ovr")
log_reg.fit(X_train, y_train)

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)

plot_decision_boundary(log_reg, axis=[4, 8.5, 1.5, 4.5])
plt.scatter(X[y==0,0], X[y==0,1])
plt.scatter(X[y==1,0], X[y==1,1])
plt.scatter(X[y==2,0], X[y==2,1])
plt.title(f"Acc:{log_reg.score(X_test, y_test):.2f}")
plt.show()

可以见OvO方式分类结果更加准确。

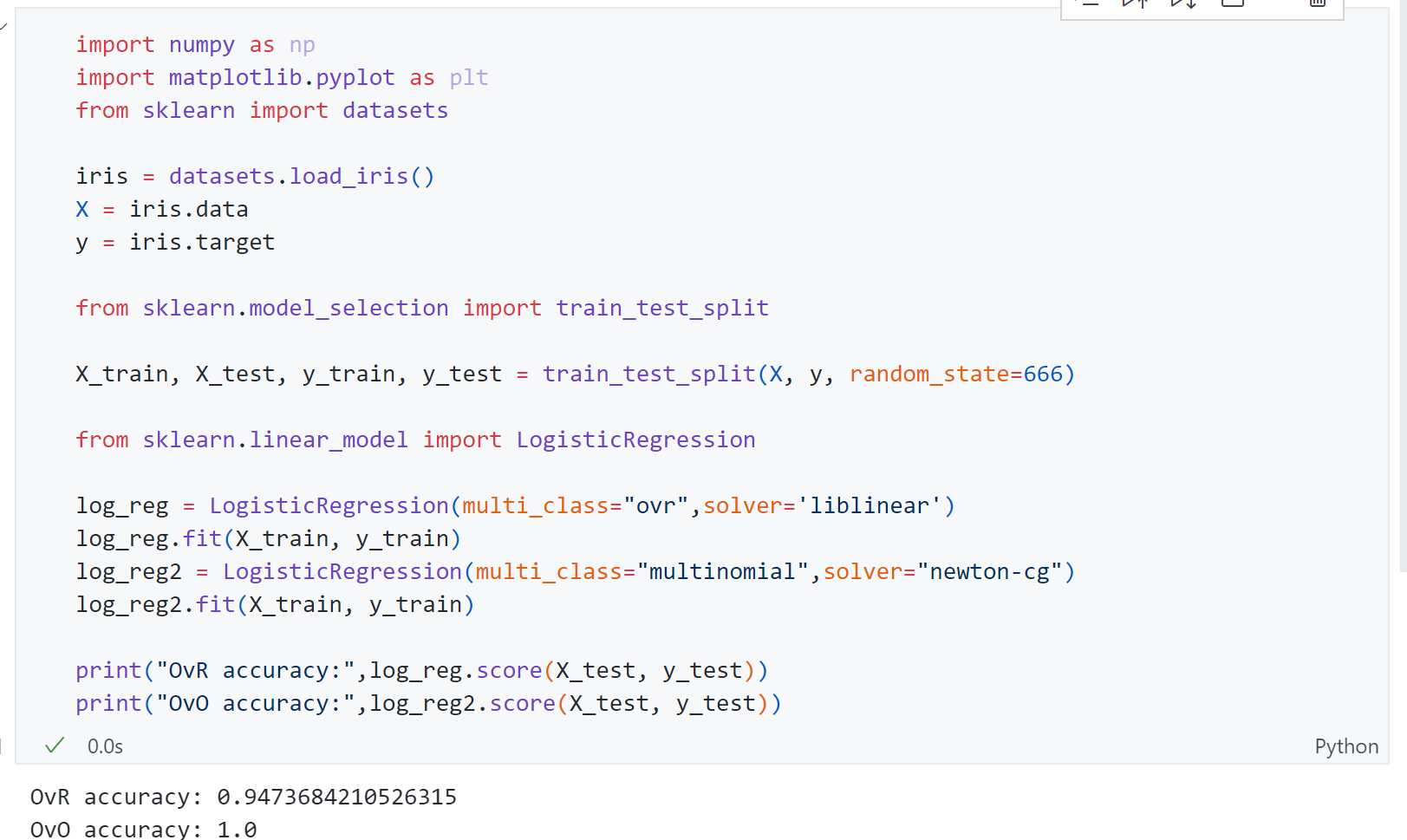
上面是为了可视化方便了只用到了iris的前两个特征，接下来看一下使用所有的特征时模型分类准确度：

可见使用上所有特征后OvR准确率为94%，而OvO为100%。

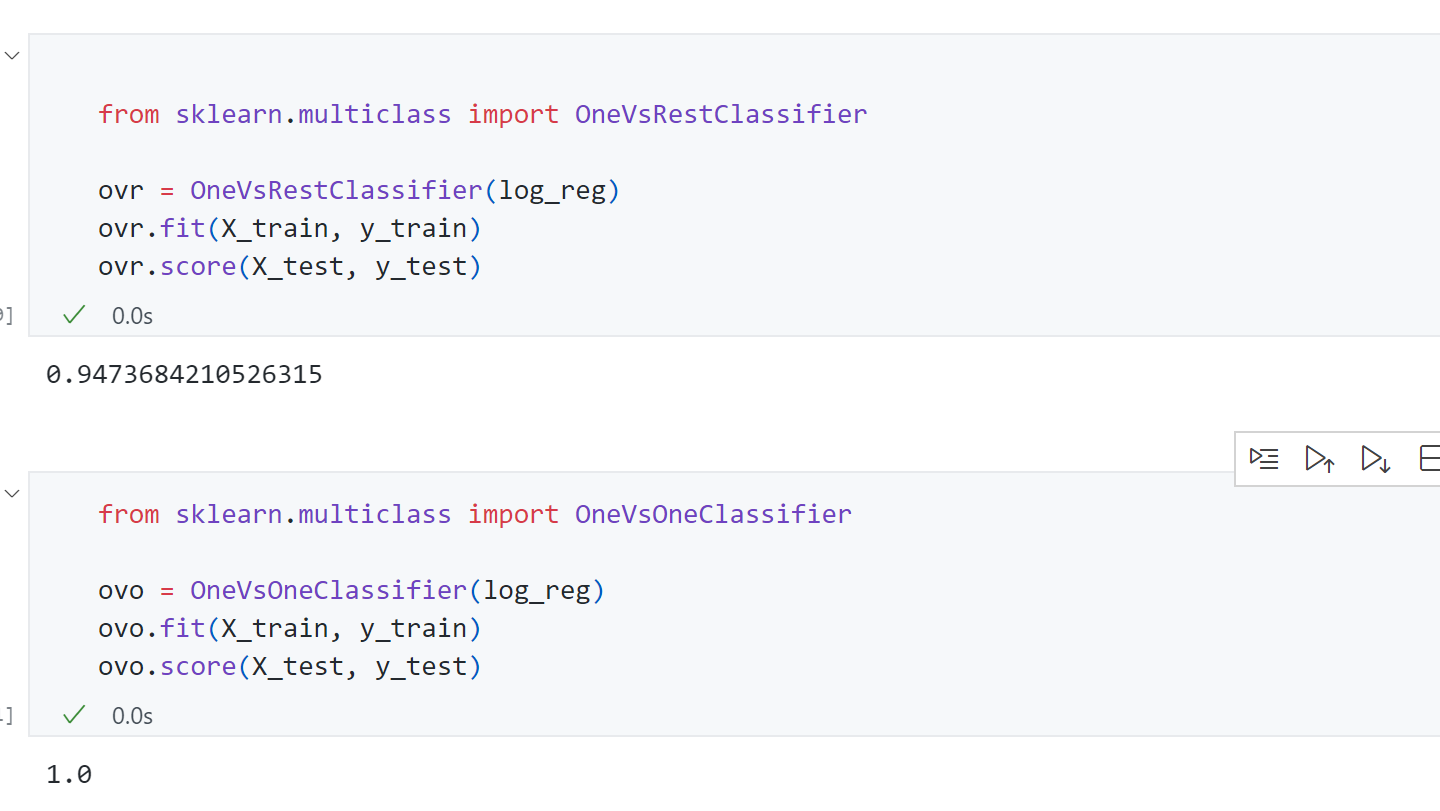
同时Scikit-learn还封装了两个类来支持OvR和OvO功能：

传入参数是一个二分类器比如LogisticRegression.