分类算法评价

分类准确度的问题

回想一下如何评价机器学习算法的好坏？对于回归问题前面介绍过MSE、MAE、RMSE、R_squared等指标，而对于分类问题上篇介绍分类算法逻辑回归以及最早介绍的KNN算法时只用到了分类准确度一个指标，那么对于分类问题这个指标足够好吗？其实这个指标存在一定的问题：

  • 假如有一个癌症预测系统，输入体检信息，可以判断是否有癌症。我们训练的模型预测准确度达到了99.9%,这样的系统是一个好的系统还是一个坏系统呢？

从准确度上看这似乎是一个很好的系统，但实际不然。为什么这样说呢？如果实际情况下癌症产生的概率只有0.1%，那么意味着不需要任何机器学习算法，对于任何体检信息，我们的系统预测所有人都是健康，即可达99.9%的准确率。极端一点，如果癌症产生的概率只有0.01%，此时我们的系统预测所有人都是健康，即可达99.99%的准确率.如果此时用机器学算法训练预测准确度是99.9%,这意味着机器学习系统是失败的，因为其比纯粹的预测99.99%的准确度还要更低。

显然上面这个例子就是分类准确度的问题所。换句话说，对于极度偏斜(Skewed Data)的数据(癌症患者相比健康人的数量极少)，只使用分类准确度是远远不够的。

因此我们要引入其它的指标来判断分类算法到底是好是坏，我们需要其它的指标来在这种极度偏斜的情况下也可以容易评价分类算法的好坏。

混淆矩阵

由上面的问题先引入混淆矩阵(Confusion Matrix)，混淆矩阵能够直观展示模型的预测结果与真实标签之间的对比关系。

先来看看对于二分类问题的混淆矩阵：

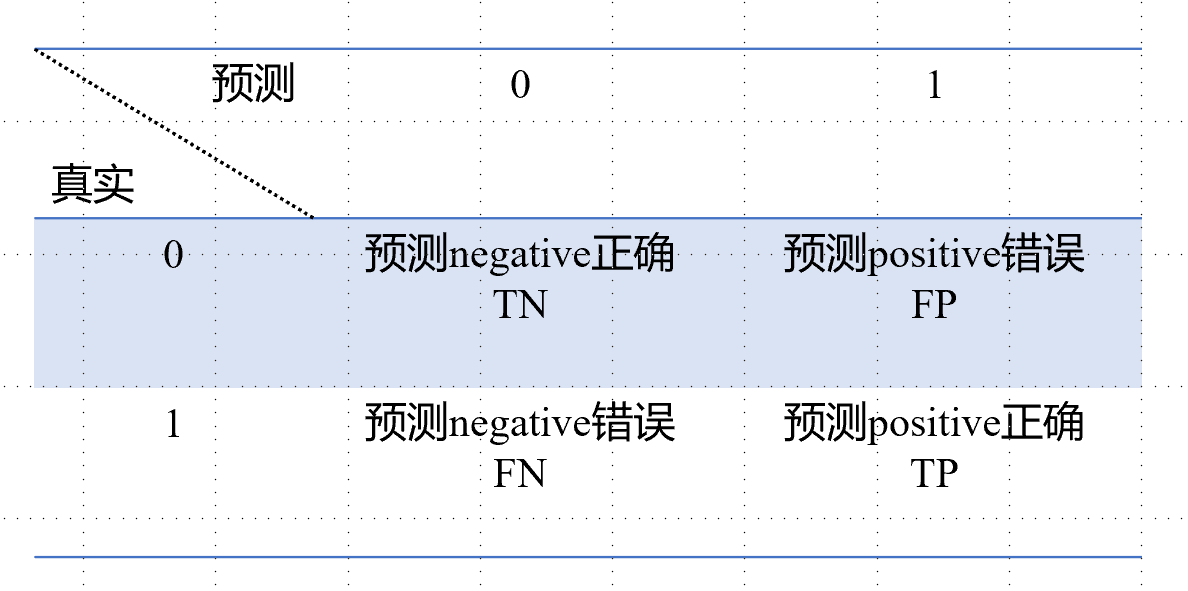
image-20251017220409709

二分类问题混淆矩阵是一个2*2的矩阵，行代表真实值，列代表预测值，通常将0称为Negative,1称为Positive.

  • TN、TP分别代表预测negative、positive正确，简单来说就是原本是0类，预测也是0类；原本是1类预测也是1类。、
  • FP代表预测positive错误，即原本是0类预测成了1类；而FN代表预测negative错误，即原本是1类预测成了0类.

举个例子：假设有10000个人，还是癌症的场景，其中0代表Negative即”不患病“，1代表Positive即”患病“.

有如下混淆矩阵：

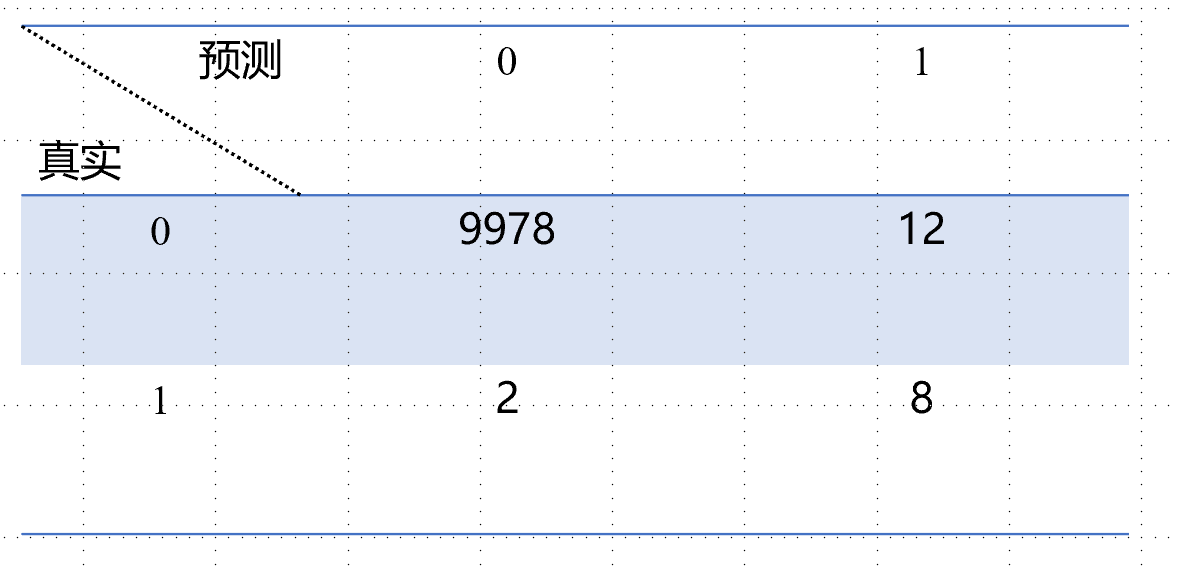
image-20251017221124232
  • 有9978个人本身negative即”不患病“，同时算法预测也”不患病“，即TN
  • 有12个人本身negative即”不患病“，但算法犯错误，预测为”患病“，即FP
  • 有2个人本身Positive即”患病“，但算法犯错误，预测为”不患病“，即FN
  • 有8个人本身Positive即”患病“，算法也准确识别为”患病“，即TP

通过上面例子基本可以理解混淆矩阵的含义了，那么通过混淆矩阵可以创建什么指标来帮助我们更好的评价分类算法呢？

精准率和召回率

精准率（Precision） 和 召回率（Recall） 是分类模型中最核心的两个指标之一，它们都源自混淆矩阵。

精准率表达式：

precision=TPTP+FPprecision=\frac{TP}{TP+FP}

其含义为在模型预测为“正”的样本中，有多少是真的“正”。对上面的例子使用这个公式可以得到precision=8/(8+12)=0.4precision=8/(8+12)=0.4 ,意味着模型预测为“患病”的人里，有40%是真的。

召回率表达式：

Recall=TPTP+FNRecall=\frac{TP}{TP+FN}

其含义为所有真实为“正”的样本中，有多少被模型找出来了。对上面的例子使召回率个公式可以得到recall=8/(8+2)=0.8recall=8/(8+2)=0.8 ,意味着 模型成功检测出了80%的病人。

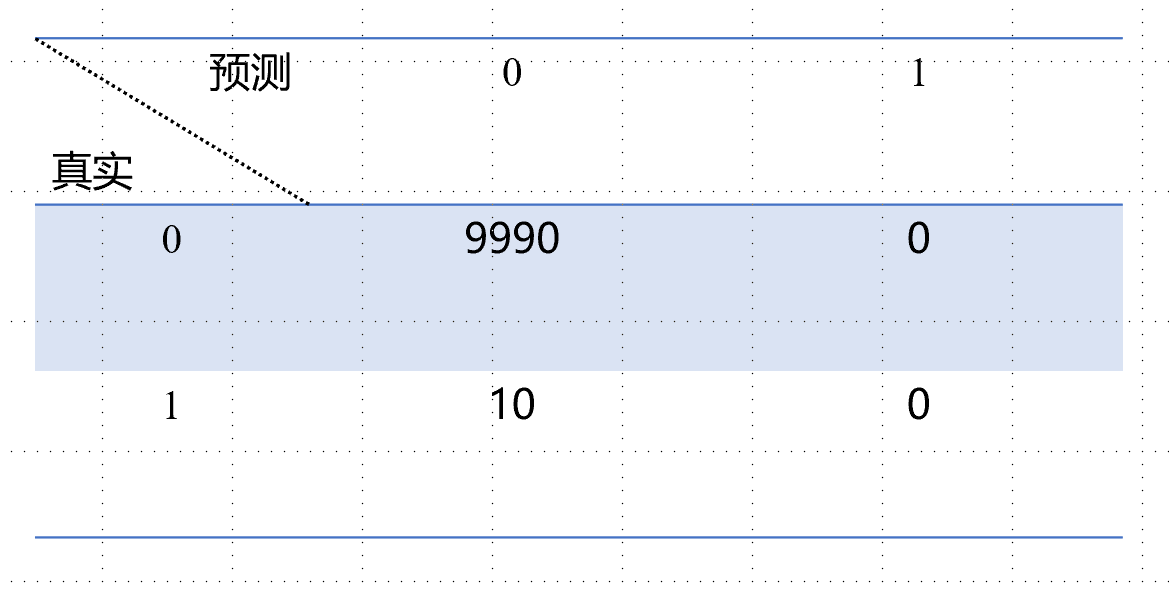
还是假设有10000个人，我们预测所有的人都是健康的，此时有99.99%的准确率，此时精准率0/(0+0)0/(0+0) 无意义，而召回率0/(10+0)0/(10+0) 也为0，显然这个预测算法毫无意义没有用，这就是精准率和召回率的意义，在极度偏斜的数据中更好的评价模型的好坏。

image-20251017232203572

编程实现：

  • 加载sklearn中的手写数字数据集，为了使数据产生偏斜，将所有非9的数字全部归为0类，所有为9的数字归为1类
1
2
3
4
5
6
7
8
9
10
11
12
13
import numpy as np
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

显然此时成了一个二分类问题。

  • 使用逻辑回归进行训练测试
1
2
3
4
5
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)

最终分类准确率为97.5%. 但因为我们处理的数据此时是极端偏斜的，即使猜测所有测试样本都不是9，也有90%的准确率，因此需要考察其它的性能指标即精准率和召回率。

  • 精准率和召回率及混淆矩阵实现：
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
y_log_predict = log_reg.predict(X_test)
def TN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 0))

def FP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 0) & (y_predict == 1))
    
def FN(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 0))
    
def TP(y_true, y_predict):
    assert len(y_true) == len(y_predict)
    return np.sum((y_true == 1) & (y_predict == 1))

print("TP:", TP(y_test, y_log_predict))
print("FN:", FN(y_test, y_log_predict))
print("FP:", FP(y_test, y_log_predict))
print("TN:", TN(y_test, y_log_predict))

结果TP:36,FN:9,FP:2,TN:403TP:36,FN:9,FP:2,TN:403, 接下来可以求出混淆矩阵、精准率和召回率：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
def confusion_matrix(y_true, y_predict):
    return np.array([
        [TN(y_true, y_predict), FP(y_true, y_predict)],
        [FN(y_true, y_predict), TP(y_true, y_predict)]
    ])

def precision_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fp = FP(y_true, y_predict)
    try:
        return tp / (tp + fp)
    except:
        return 0.0
        
def recall_score(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)
    try:
        return tp / (tp + fn)
    except:
        return 0.0
    
print(confusion_matrix(y_test, y_log_predict)) 
print(recall_score(y_test, y_log_predict))
print(precision_score(y_test, y_log_predict))

结果为：

ConfusionMatrix=(4032936)recallsocre=0.8precisionsocre=0.95Confusion\quad Matrix =\begin{pmatrix} 403 & 2\\ 9 & 36 \end{pmatrix}\\ recall \quad socre=0.8\\ precision \quad socre=0.95

Scikit-learn中的混淆矩阵、精准率和召回率：

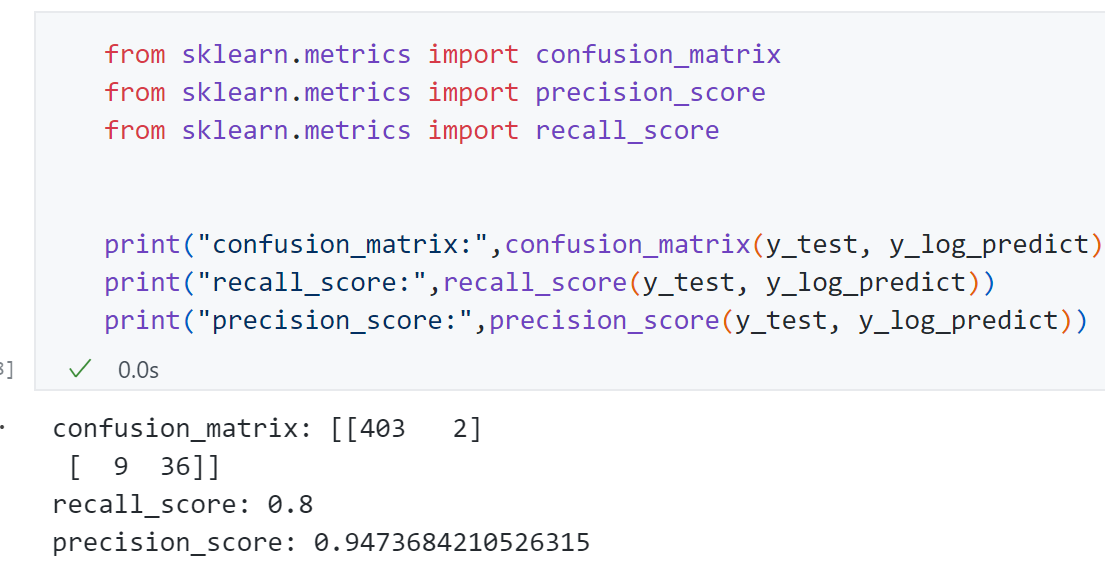
image-20251018131602670

可见Scikit-learn的结果与我们实现的结果一致。

接下来思考一下如果具体训练一个分类算法，对这两个指标如何解读呢？ 或者对于同一个算法的两组超参数，这两个指标出现了差异，比如一组精准率高召回率低，另一组精准率低召回率高，那么此时两种算法如何取舍呢？

F1 Score

对于二分类问题，如果数据是极度偏斜的，使用精准率和召回率这两个指标比使用准确率指标要好。但是这是两个指标，两个指标之间可能会产生差异，有些算法精准率低召回率高，有些精准率高召回率低，那么具体如何解读这两个指标？主要根据使用场景来定。

  • 精准率比召回率更重要的场景：比如股票预测场景，还是一个二分类问题，1代表股票升，0代表股票降。我们会更注重精准率TP/(TP+FP)TP/(TP+FP)，这个比率越高越好，因为精准率代表我们预测会升的股票中有多少升了，核心是因为我们会购买我们预测升的股票，所以这些里面越多升越好,而FP是我们预测会升的股票它反而降了，会导致亏钱。但对于召回率TP/(TP+FN)TP/(TP+FN)，其代表升的股票中有多少我们预测对了，对于FN是指本身会上升的股票我们预测它不会升，给落掉了，但并不会因此亏钱，因为我们不会投钱进去。

  • 召回率比精准率更重要的场景：比如病人诊断场景，对于召回率TP/(TP+FN)TP/(TP+FN)，其中FN代表本来得病的人但我们没预测出来，这样会导致病人结果恶化下去，因此关注召回率即不想漏掉真正患病的人。但精准率TP/(TP+FP)TP/(TP+FP)低一些没有关系，因为 FP代表本来没病的人但我们预测有病，但这些人群做进一步检查确诊就好了，FP的错误只是让这些人多做了一些检查而已。

因此不同应用场景我们会偏好不同的指标，不过还有很多情况不像上面的例子那么极端，我们可能更希望获得两个指标的一个平衡，即希望同时关注精准率和召回率，这就引入了新的指标F1 Score.

F1 Score要兼顾精准率和召回率两个指标：

F1=2.precision.recallprecision+recall[0,1]调和平均值:1F1=12(1precision+1recall)F_1=\frac{2.precision.recall}{precision+recall}\quad[0,1]\\ 调和平均值:\frac{1}{F_1}=\frac{1}{2}(\frac{1}{precision}+\frac{1}{recall})

上面这个式子代表F1 Score是recall和precision的调和平均值。同时很显然F1 Score 取值范围为[0,1].

为什么取调和平均值而不是算数平均值？

调和平均值的特点是如果两个指标极度不平衡，比如一个值特别高一个值特别低，最终得到的F1 Score也将特别低，只有两者都非常高最终得到的F1 Score才会高，而算数平均值相反。

编程实现：

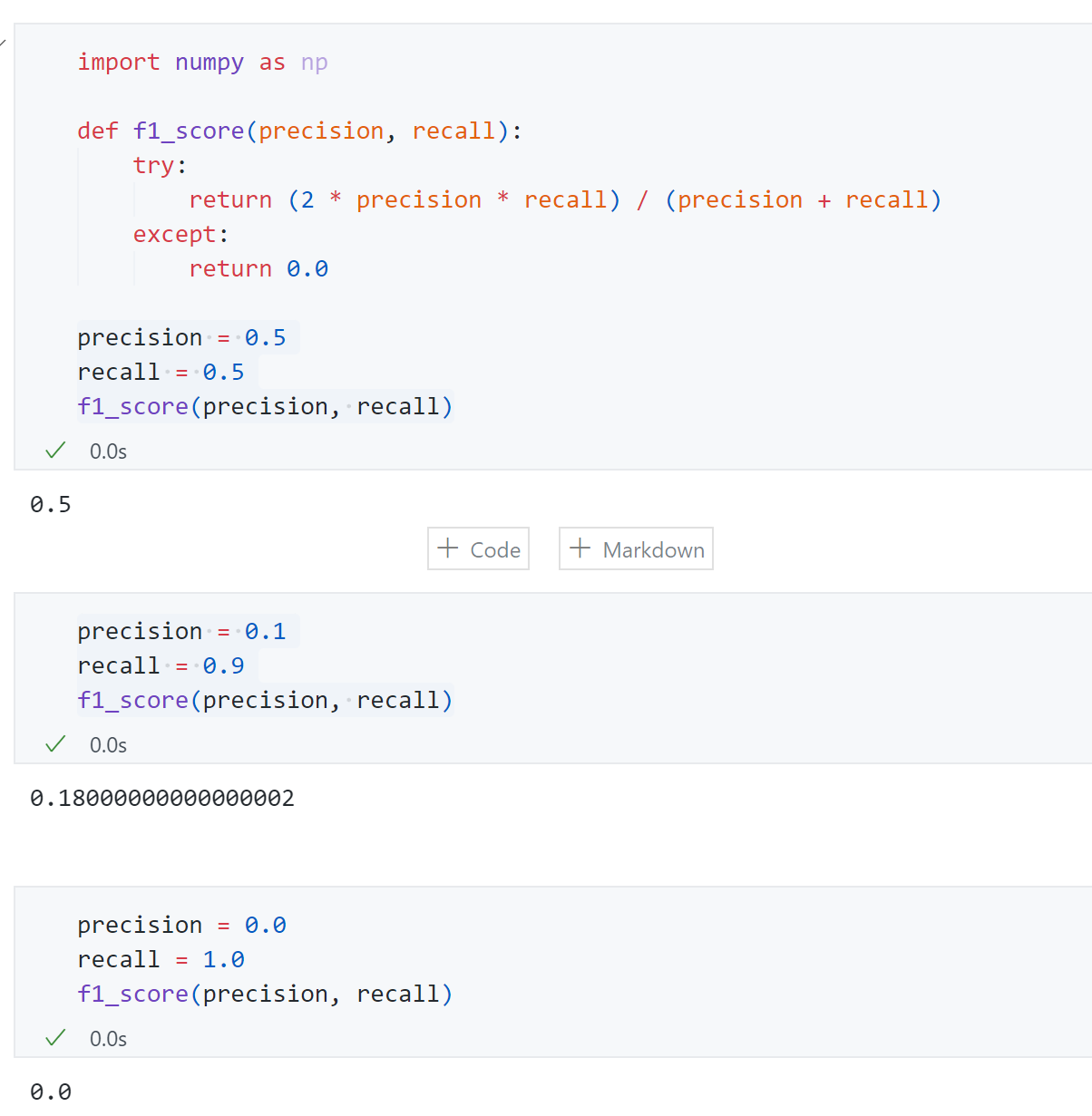
image-20251018135744208

可以发现:

  • recall=precision=0.5recall=precision=0.5 时f1_score=0.5f1\_score=0.5 ,因为代入式子可得此时F1=precision=recallF_1=precision=recall
  • recall=0.9,precision=0.1recall=0.9,precision=0.1 时f1_score=0.18f1\_score=0.18 ,如果用算数平均值此时F1=0.5F_1=0.5,但用调和平均值F1=0.18F_1=0.18远远小于0.5，这就是调和平均值的优势，两者有一个小都会拉低F1F_1 的结果
  • .recall=1.0,precision=0.0recall=1.0,precision=0.0 时f1_score=0.0f1\_score=0.0 更说明如此

应用到上面的极度偏斜手写数字数据中：

ConfusionMatrix=(4032936)recallsocre=0.8precisionsocre=0.95f1score=(0.8∗0.95)/(0.8+0.95)=0.868Confusion\quad Matrix =\begin{pmatrix} 403 & 2\\ 9 & 36 \end{pmatrix}\\ recall \quad socre=0.8\\ precision \quad socre=0.95\\ f1\quad score = (0.8*0.95)/(0.8+0.95)=0.868

精准率和召回率平衡

一些场景使用分类算法可能更注重精准率，而另外一些场景可能更加注重召回率，还有一些场景使用F1scoreF1 score 综合两个指标，希望两者越大越好。但其实对于一个分类系统，使两个指标同时都大这一目标可能实现不了，两者是相互矛盾的，如果使精准率提高召回率就不可避免的下降，如果使召回率提高精准率就不可避免下降。我们要做的是找到两个指标的一个平衡。

为什么精准率和召回率两者相互矛盾？

上篇讲到逻辑回归的决策边界为：

θT.xb=0\theta^T.x_b=0

接下令这个决策边界等于一个阈值：

θT.xb=threshold\theta^T.x_b=threshold

将这个阈值threshhold作为决策边界相当于平移决策边界对应的那根直线从而影响分类结果。

接下来看下这个threshold取不同的值是如何影响分类结果：

三角代表1，圆代表0

image-20251018163336804

  • 如果以图中黑线(threshold=0)作为分类阈值(图中黑线)的话，此时precision=4/5=0.8,recall=4/6=0.67precision=4/5=0.8,recall=4/6=0.67

  • 如果以图中红线(threshold>0,分类阈值变大)作为分类阈值的话，此时precision=2/2=1.0,recall=2/6=0.33precision=2/2=1.0,recall=2/6=0.33

  • 如果以图中绿线(threshold<0,分类阈值变小)作为分类阈值的话，此时precision=6/8=0.75,recall=6/6=1.0precision=6/8=0.75,recall=6/6=1.0

总体来看上面的图，沿着score方向即随着score增大，precision逐渐增高，recall逐渐降低，互相矛盾。如果想要提高precision,那么相应对特别有把握的数据分类为1，这种情况就会导致很多真实为1的样本被排除在外，如图中红线情况，因此召回率降低。反之如果要升高召回率，那么相应降低判断的概率，比如癌症预测系统中患者有10%患癌可能性都判定为一个癌症患者相应做进一步确诊，此时召回率确实得到了提高但精准率相应下降。

总的来说，精准率和召回率是一对互相制约、相互平衡的指标。

那么具体做分类问题这个threshold如何选取呢？

PR曲线

尝试用可视化的方式绘制精准率和召回率随着阈值threshold改变的曲线：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target.copy()

y[digits.target==9] = 1
y[digits.target!=9] = 0

from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)

from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
decision_scores = log_reg.decision_function(X_test)

from sklearn.metrics import precision_score
from sklearn.metrics import recall_score

precisions = []
recalls = []
thresholds = np.arange(np.min(decision_scores), np.max(decision_scores), 0.1)
for threshold in thresholds:
    y_predict = np.array(decision_scores >= threshold, dtype='int')
    precisions.append(precision_score(y_test, y_predict))
    recalls.append(recall_score(y_test, y_predict))
 
plt.plot(thresholds, precisions)
plt.plot(thresholds, recalls)
plt.show()

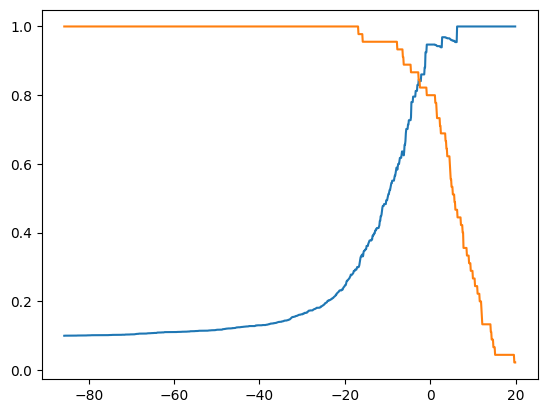
image-20251018180830097

其中横轴代阈值threshold，纵轴代表precision和recall的取值[0,1].

可以发现蓝色曲线precision随着threshold增大不断增大，橙色曲线recall随着threshold增大不断减小，跟上一张图所讲的一致。有了这个曲线我们就可以根据我们希望的目标比如希望精确率95%来找到对应的threshold.

1
decision_scores = log_reg.decision_function(X_test)

值得一提上面代码中decision_scores即逻辑回归σ(θT.xb)\sigma(\theta^T.x_b) 中θT.xb\theta^T.x_b 的值，此时还未经过sigmoid输出概率。

然后是Precision-Recall即PR曲线：

1
2
plt.plot(precisions, recalls)
plt.show()
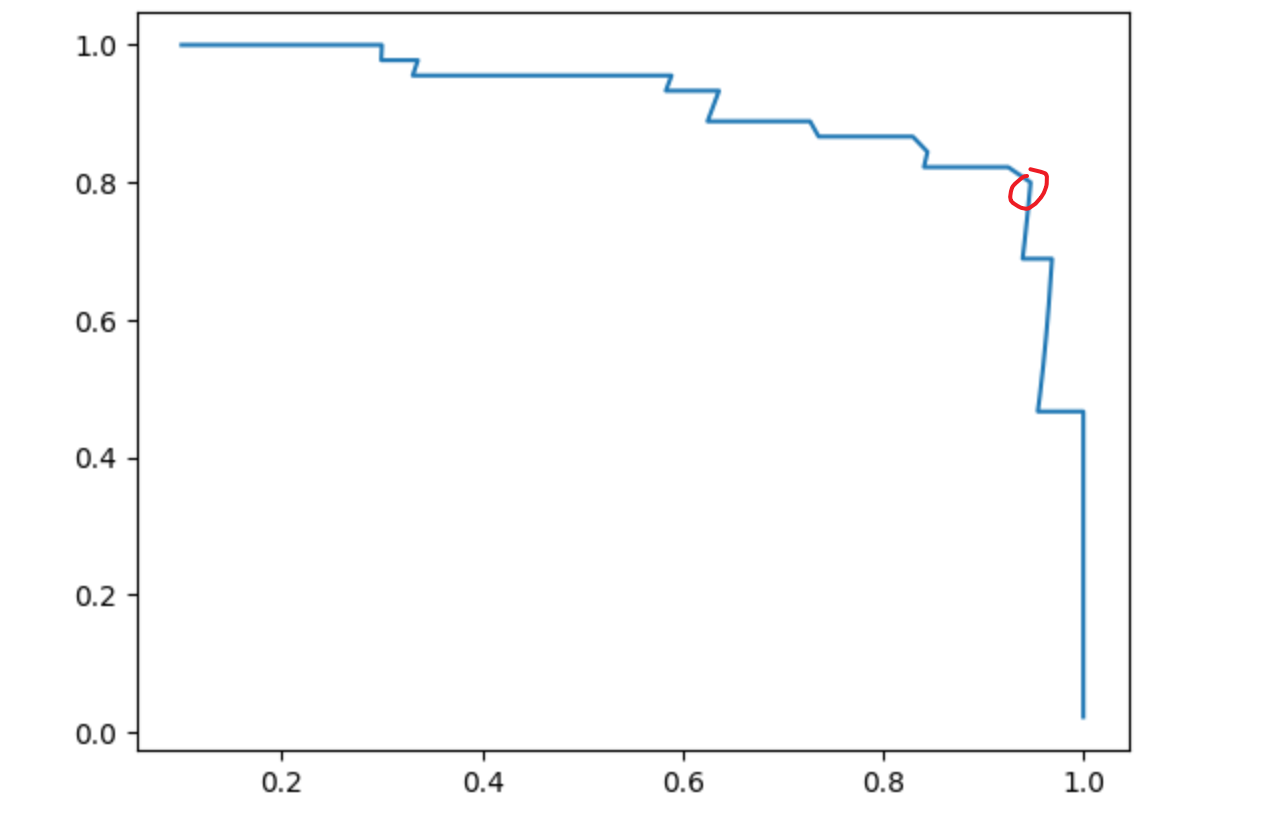
image-20251018181920397

可见，随着precisions逐渐增大，recalls不断减小。同时可以发现有一个急剧下降的点，这个点可能就是精准率和召回率相较而言一个最好的平衡位置。

采用sklearn绘制这两个曲线：

1
2
3
4
5
6
7
8
9
10
from sklearn.metrics import precision_recall_curve

precisions, recalls, thresholds = precision_recall_curve(y_test, decision_scores)

plt.plot(thresholds, precisions[:-1])
plt.plot(thresholds, recalls[:-1])
plt.show()

plt.plot(precisions, recalls)
plt.show()

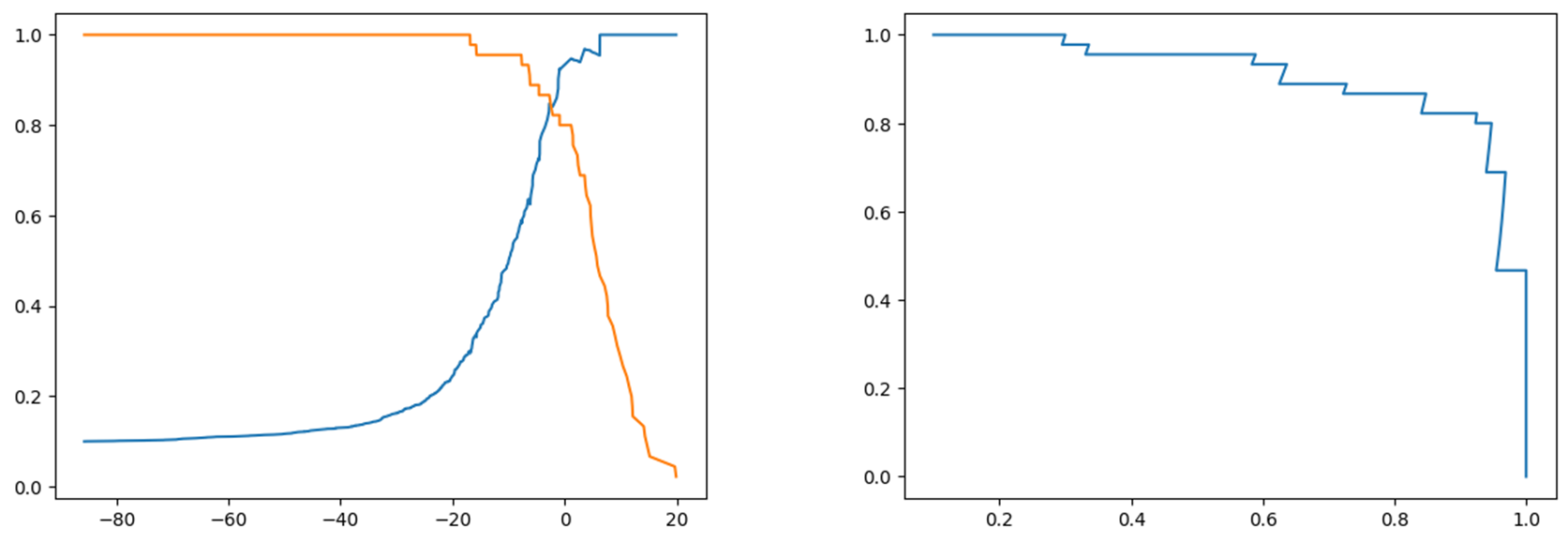
image-20251018182144687

所以PR曲线整体形状如下图：

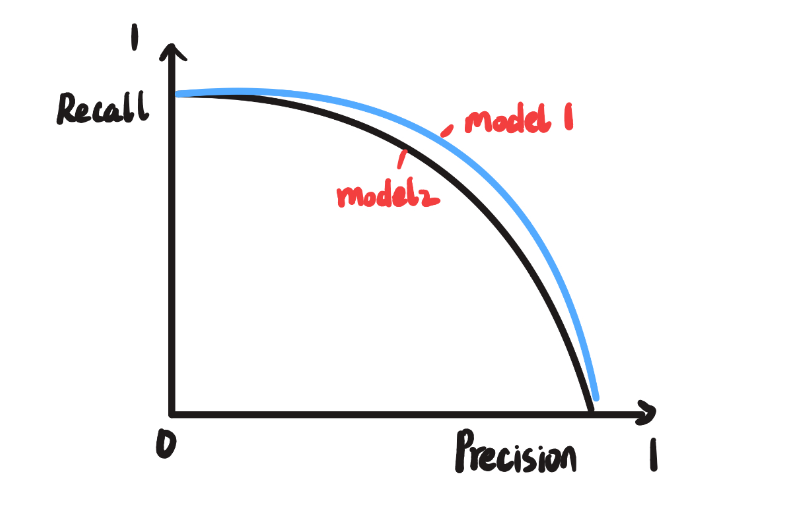
3dc3c9ac7909178c20e2c3743f7bfb63

随着Precision升高Recall不断降低，如果有两个模型对应两条曲线如图中的蓝线和黑线，蓝线整体在黑线的外面，因此Model 1优于Model 2，因为在蓝线每一个点对应的Precision和Recall都高于黑线，因此PR曲线还能用于选择模型。

ROC曲线

ROC曲线全称Receiver Operation Characteristic Curve,描述的是TPR和FPR之间的关系。

什么是TPR和FPR？

  • TPR是True Positive Rate的缩写，即Recall
  • FPR是False Positive Rate的缩写，即FPR=FP/(TN+FP)

同理绘制这个图：

image-20251018184239116

可见TPR和FPR之间呈现着一个相一致的趋势，TPR越高相应的FPR也越高，TPR越低FPR也越低。

编程实现：

  • TPR和FPR实现
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
def TPR(y_true, y_predict):
    tp = TP(y_true, y_predict)
    fn = FN(y_true, y_predict)
    try:
        return tp / (tp + fn)
    except:
        return 0.

def FPR(y_true, y_predict):
    fp = FP(y_true, y_predict)
    tn = TN(y_true, y_predict)
    try:
        return fp / (fp + tn)
    except:
        return 0.

同理绘制出ROC曲线(代码省略，把上面函数代入，替换上面PR曲线的代码即可)，ROC曲线的横轴纵轴分别为FPRS和TPRS：

image-20251018190059659

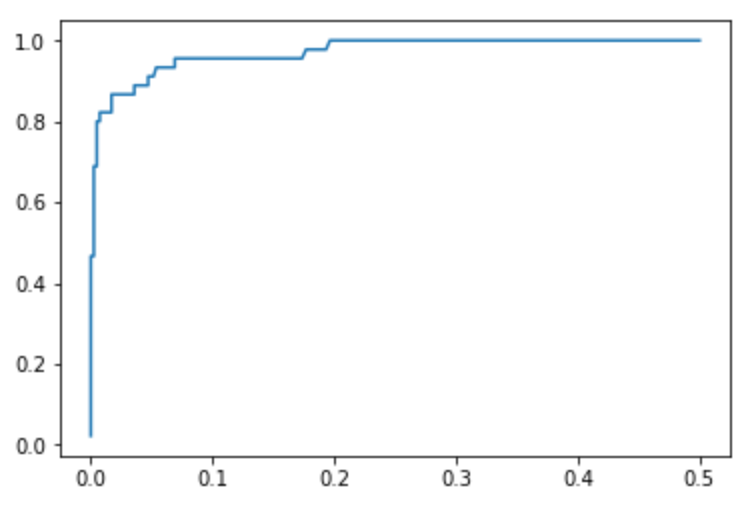
scikit-learn中的ROC曲线实现：

1
2
3
4
5
from sklearn.metrics import roc_curve

fprs, tprs, thresholds = roc_curve(y_test, decision_scores)
plt.plot(fprs, tprs)
plt.show()
image-20251018190338833

显然针对这个ROC曲线，其面积越大说明分类算法更好。横轴代表FPRS，横轴越小代表FP越小，纵轴代表TPRS, 此时如果纵轴值越大代表TP越大，显然此时面积会更大，分类算也更好。这个面积叫做AUC即Area Under Curve.

1
2
3
from sklearn.metrics import roc_auc_score

roc_auc_score(y_test, decision_scores)

输出AUC=0.983.

同理ROC曲线大致是下面的形式，也可以用来模型选择，其中蓝线与坐标轴所围的面积AUC相比红线更大，因此蓝线分类模型更好。

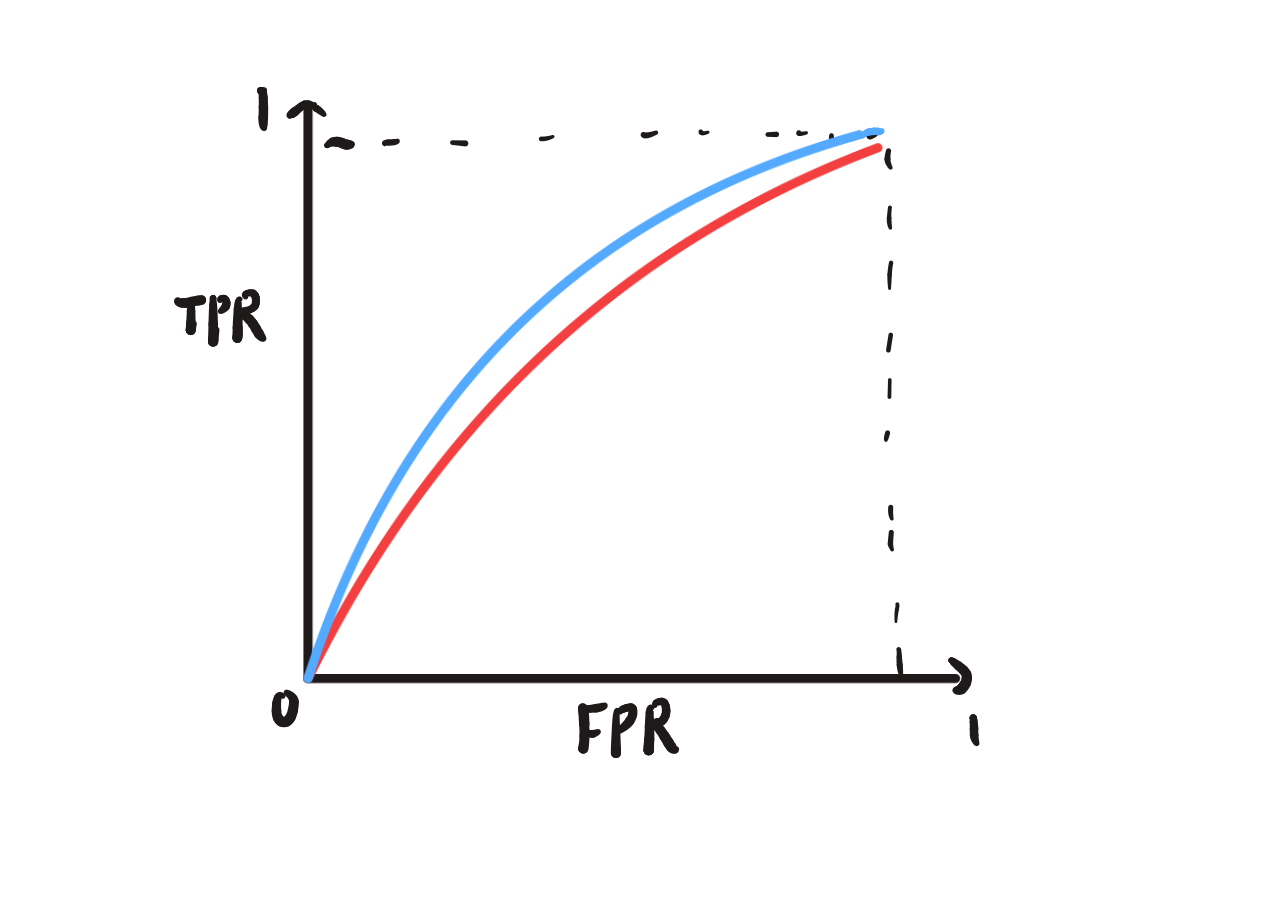
34a2af19c49cc9cc0ffd6a8cd5701567

多分类问题的混淆矩阵

  • 这里采用digits的0-9一共10个数字类别的数据，与前面相比并未进行数据偏斜处理。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
import numpy as np
import matplotlib.pyplot as plt
from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target
from sklearn.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.8, random_state=666)
from sklearn.linear_model import LogisticRegression

log_reg = LogisticRegression()
log_reg.fit(X_train, y_train)
log_reg.score(X_test, y_test)  #  0.93115438108484005

y_predict = log_reg.predict(X_test)
from sklearn.metrics import precision_score

precision_score(y_test, y_predict, average="micro") # 0.93115438108484005

逻辑回归默认采用OvR的方式处理多分类问题，准确率93%,精准率也为93%。

绘制出10分类问题的混淆矩阵：

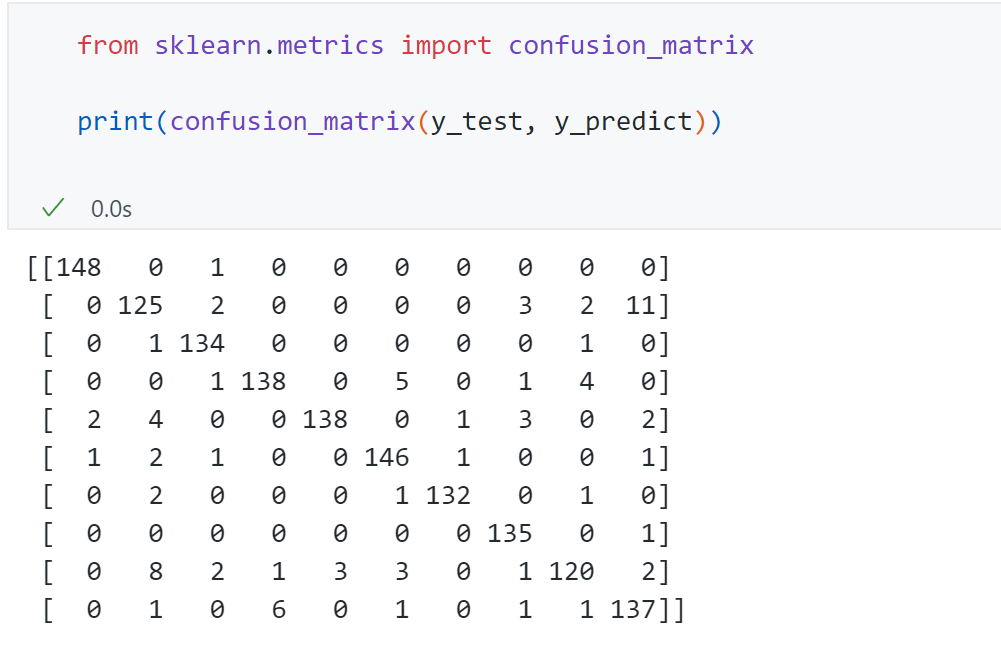
image-20251018192622209

矩阵每个元素aija_{ij} 代表真值为i预测为j的数量，对角线位置即真值为0-9，预测值为0-9的数量。可以发现大部分样本位于对角线，也反映了模型分类效果比较好。

将混淆矩阵可视化：

1
2
3
cfm = confusion_matrix(y_test, y_predict)
plt.matshow(cfm, cmap=plt.cm.gray)
plt.show()

image-20251018193013248

越亮代表数字越大，越暗代表数字越小，通过可视化可以直观看出模型预测好坏的位置，可以发现对角线位置是最亮的。但是关注预测正确的部分是没有意义的，我么真正想找的是预测错误的地方。

可以做如下处理：

1
2
3
4
5
6
row_sums = np.sum(cfm, axis=1)
err_matrix = cfm / row_sums
np.fill_diagonal(err_matrix, 0) # 对角线位置填0

plt.matshow(err_matrix, cmap=plt.cm.gray)
plt.show()

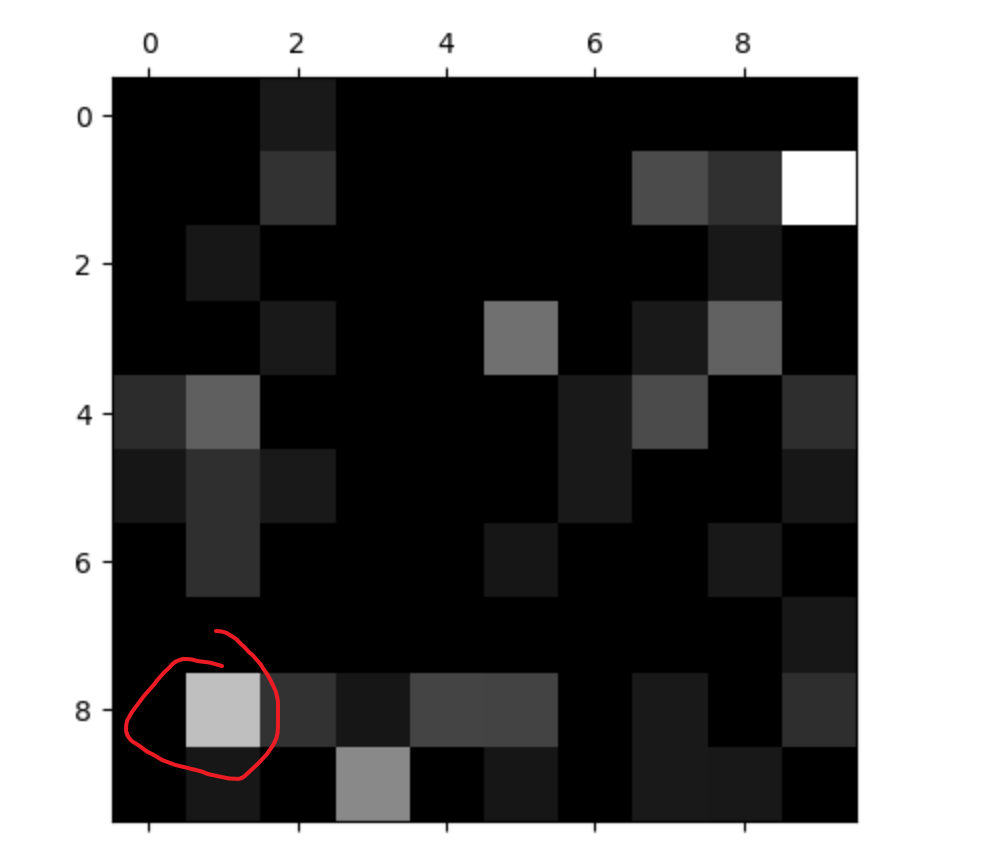
将对角线位置填0，即除去了预测正确的样本，剩下的都是预测错误的样本。然后每一行的数字除以每一行的代数和进行可视化，就能明显看出预测错误的地方。越亮的地方代表犯错越多的地方。比如我红圈地方代表真实为8的地方很多预测成了数字1.

一些思考

PR曲线对偏斜数据更敏感，那为什么不选择用PR曲线而要使用ROC曲线呢？选择的标准是什么？

这里我引用 一下liuyubobobo老师的回答，因为很经典，所以我放在这里。

首先需要明确一点：在机器学习领域，对于指标，很多时候不是选择谁的问题，而是在可能的情况下，所有的指标都应该看一看，以确定训练的模型是否有问题。这就好比在医院检查身体，不是先确定要看哪个指标，然后就只看这个指标；而是尽可能去看所有指标。因为任何一个指标存在问题，都可能意味着你的身体的某个机能存在问题。

所以，我们的目的不是“找到”单一的“最好”的指标；而是了解所有的指标背后在反映什么，在看到这个指标出现问题的时候，能够判断问题可能出现在哪里，进而改进我们的模型。虽然我们的改进方向可能是单一的。这就好比在医院看病，我们主要症状可能是发烧，此时，我们的主要异常指标是“温度”，所以我们主要尝试使用可以“降温”的治疗手段，但这不代表我们在治疗的过程中对其他指标不管不顾，只要把温度降到正常水平就可以了。在尝试“降温”的过程中，如果我们发现血压，心跳，白血球，红血球，任何一个指标出现异常，我们都需要马上做出相应的反应。

具体到PR曲线和ROC曲线，他们的核心区别在TN。可以看出来，PR曲线其实不反应TN。所以，如果你的应用场景中，如果TN并不重要，那么PR曲线是一个很好的指标（事实上，Precision和Recall就是通过抹去TN，来去除极度的偏斜数据带来的影响，进而放大FP, FN和TP三者的关系的）。

而ROC曲线则综合了TN, FP, FN和TP。虽然它对TN极度多的情况下，FP，FN和TP的变化不敏感。所以在TN没有那么多（数据没有那么偏斜），或者TN是一种很重要的需要考虑的情况下，ROC能反映出PR不能反映的问题。