算法与数据结构(1):线性查找法

Linear Search

什么是算法

算法的英文名称为Algorithm, 其本意是解决问题的方法。不过算法这个词更多的应用在计算机领域中，在计算机领域中算法更明确的定义是一系列解决问题的，清晰，可执行的计算机指令。

生活中我们也会接触类似算法的概念。举个例子，比如一个人第一次去北京想去天安门，下了火车站可能会问路：如何去天安门？路人可能会回答先坐地铁到哪一站，然后换乘公或者地铁再到哪，最后步行到天安门，这一系列的指令本质就是算法，它在解决如何从火车站到达太天安门广场的问题。

再举一个比较贴切生活的例子就是做菜，比如我想要做一道鱼香茄子，步骤如下：

• 1.茄子洗净切成4厘米长的段，提前用盐抓一下让茄子变软。
• 2.葱姜蒜切末。
• 3.锅烧热放一点点油，倒入用盐抓过的茄条
• 4.快速翻炒将切条煸炒变软。捞出待用。
• 5.将锅烧热，放入油。煸香姜末和蒜末，放入猪肉馅翻炒。
• 6.翻炒到猪肉馅断生、炒出香味，加入葱花。放入剁碎的豆瓣酱翻炒，炒出香味和红油再烹入料酒。
• 7.放入煸软的茄条，加白糖、酱油调味翻炒均匀融合香味。
• 8.用少许水淀粉勾薄芡、加入蒜茸，放少许醋。翻炒均匀即可出锅装盘。

上面这个来自香哈网的菜谱，吐槽一下：咱也不知道为啥鱼香茄子会用猪肉😂.这个整个做菜的步骤过程就可以理解成一个算法.

算法的五大特性：

• 有限性：一个算法不应该是无限循环的，应该在有限的时间里可以执行完。这里有限的时间不代表时间一定会非常短，如果设计一个算法需要一万年才能执行完，从原则上讲它也是一个算法，只不过时间太长算法不太实用。随着硬件技术发展，这个算法可能以后只需要1s就能执行完，另外我们研究算法恰似是从一个看似不可行的算法出发一步一步优化得到可行的算法，因此这种看似不可行的算法可能是有研究意义的。
• 确定性：不会产生二义性。比如计算学生成绩，如果算法步骤的一步是“取出成绩最高的学生”，那么这就是二义性的，这里是语文成绩最高还是数学成绩最高亦或是总成绩最高？算法的每一个指令都应该是清晰的。
• 可行性：算法的每一步应该是可行的。比如算法某一步是拿出最大的质数，这显然是不可能的，质数是无穷个的。
• 输入：一个算法是有输入的，算法的输入是更加广义的。对于一个算法其一定有要操纵的对象的，这个操纵对象就是算法的输入，其可能定义在类中、成员变量、全局变量甚至隐藏在算法的语义中，比如一个算法作用就是生成0这个数字，算法逻辑直接return 0即可.看起这个算法没有输入值，但其实必须数学上定义0是什么才能返回0，这个0概念本身就是算法的输入。
• 输出：一个算法是有输出的，即使是void类型的函数，里面可能实现了绘制一个圆，这个结果也是算法的输出。

最简单的算法：线性查找法

什么是线性查找法？我们在生活中其实经常使用线性查找法，比如在一沓试卷中找到属于自己的那张试卷，我们会从第1张试卷开始查看名字是不是自己的，不是。接着看第2张卷子，不是。接着看第3张卷子，不是。这个过程依次类推直到第n张卷子看到自己的名字就找到了。这就是线性查找法，一个一个的寻找自己想要找到的目标元素。

这个过程在计算机中如何表示的呢？对于线性查找法我们会在一个线性的数据结构中完成，比如下图在数组查找数字7：

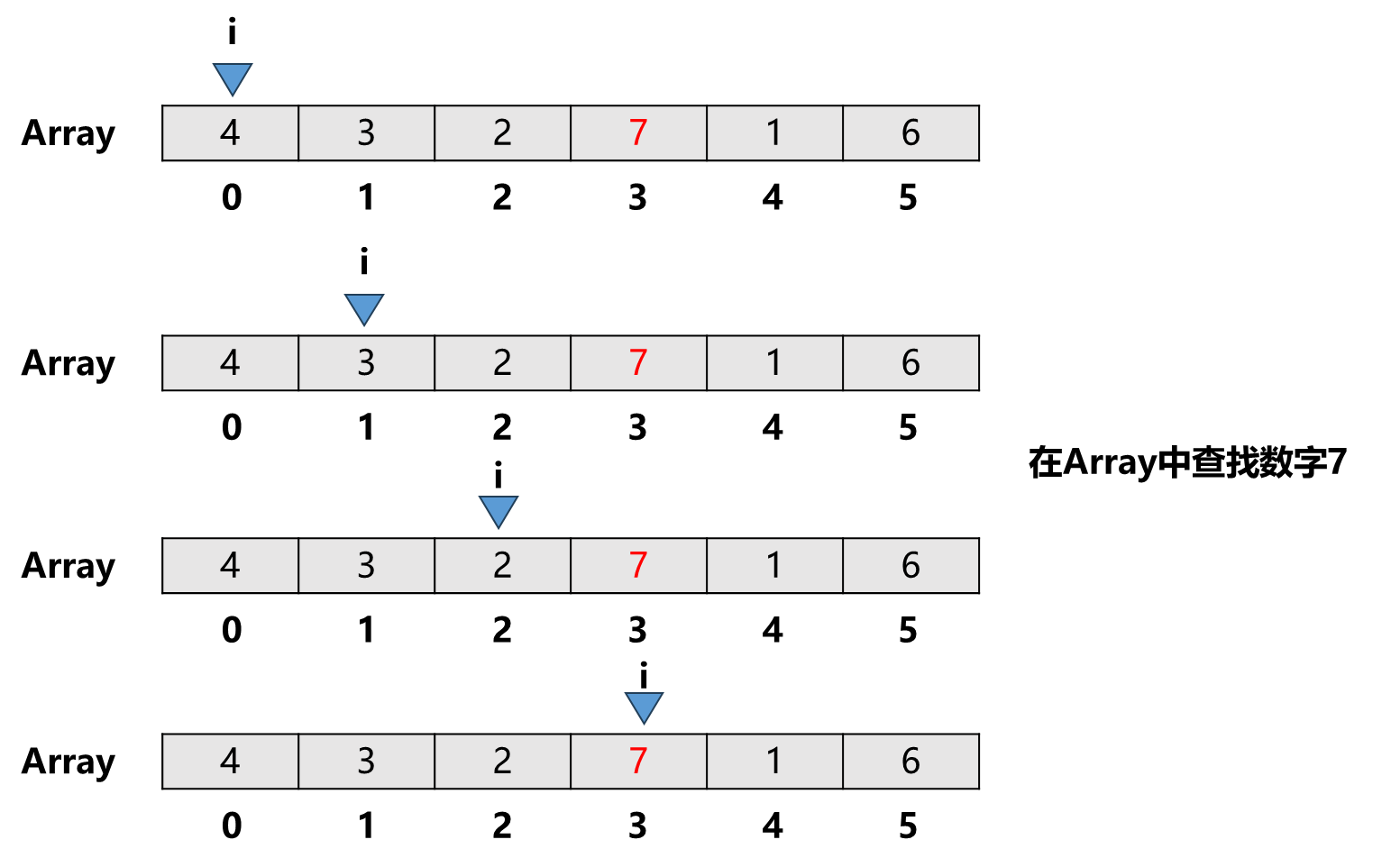
输入：数组，和目标元素

输出：目标元素所在的索引；若不存在，返回-1

实现线性查找法

以下面int类型的数组举例：

public class LinearSearch {

    private LinearSearch() {}
    public static int search(int[] data, int target){
        for(int i = 0; i < data.length; i++)
            if (data[i]==target)
                return i;

        return -1;
    }

    public static void main(String[] args) {

        int[] data = {24, 18, 12, 9, 16, 66, 32, 4};

        int res = LinearSearch.search(data, 16); 
        System.out.println(res); # 存在，返回索引4

        int res2 = LinearSearch.search(data, 7);
        System.out.println(res2); # 不存在，返回-1

    }
}

最终输出结果为4，-1.

但上面的线性查找法还有一个问题，就是只能在int类型数组中查找一个int类型的元素，还有很多的数据类型比如float, bool, char或者是我们自己创建的类型，不可能每一个类型都写一个search的方法，不能重复造轮子，那么如何解决？

处理这个问题并不困难，很多语言都有一个专门的语言特性来使得类或方法处理这种不同类型的语言机制–泛型。

泛型只能接受类对象，而不能接受基本数据类型。

• java的八种基本数据类型：boolean, byte, char, short, int, long, float, double

为了解决这个问题，java每个基本数据类型都有对应的包装类：

• Boolean, Byte, Character, Short, Integer, Long, Float, Double

因此得到一个能够处理泛型的线性查找法代码：

public class LinearSearch{

    private LinearSearch() {}
    public static <E> int search(E[] data, E target){
        for(int i = 0; i < data.length; i++)
            if (data[i].equals(target))
                return i;

        return -1;
    }

    public static void main(String[] args) {

        Integer[] data = {24, 18, 12, 9, 16, 66, 32, 4};

        int res = LinearSearch.search(data, 16);
        System.out.println(res);

        int res2 = LinearSearch.search(data, 7);
        System.out.println(res2);

    }
}

几个代码细节：

public static <E> int search(E[] data, E target)
    
Integer[] data = {24, 18, 12, 9, 16, 66, 32, 4};

首先是方法定义改成了一个泛型的方法，传入的参数也是泛型的数据类型，用E替代。同时,这里传入的数字16，7依然可以这样传，java会自动将其转化为对应的包装类，但是data数组不行，所以需要手动将int数组改为其包装类数组Integer.

if (data[i].equals(target))

此时的data[i]，target不是一个基本数据类型了，而是一个类对象，判断两个类对象相等不应该用==，因为== 判断的是引用相等，实际上这里判断的是值相等，因此改为equals方法。

同时注意对于不同的类，其equals方法具体实现逻辑有可能不同，java的8种基本类型包装类都实现了equals方法，但是使用自己定义的类的话，就需要注意需要自己再定义的类中将equals的逻辑给实现出来。

接下来使用自定义类测试我们的算法：

自定义个Student.java的类,但先不重写equals方法

public class Student {
    private String name;

    public Student(String name) {
        this.name = name;
    }
}

测试Student类：

public class LinearSearch{

    private LinearSearch() {}
    public static <E> int search(E[] data, E target){
        for(int i = 0; i < data.length; i++)
            if (data[i].equals(target))
                return i;

        return -1;
    }

    public static void main(String[] args) {

        Integer[] data = {24, 18, 12, 9, 16, 66, 32, 4};

        int res = LinearSearch.search(data, 16);
        System.out.println(res);

        int res2 = LinearSearch.search(data, 7);
        System.out.println(res2);

        Student[] students = { new Student("A"),
                new Student("B"),
                new Student("D"),
        };

        Student dong = new Student("D");
        int res3 = LinearSearch.search(students, dong);
        System.out.println(res3);

    }
}

最终返回结果-1.但是明明这个students数组里定义了"D".这就是因为自定义类Student默认的equals方法就是==，比较的是两个类对象的地址，但是我们希望比较的是两个类对象的字符串，为了实现这个逻辑就必须自定义Student的equals函数。

重写equals方法：

public class Student {
    private String name;

    public Student(String name) {
        this.name = name;
    }

    @Override
    public boolean equals(Object student) {

        if(this == student)
            return true;
        if(student == null)
            return false;
        if(this.getClass() != student.getClass())
            return false;
        
        Student another = (Student)student;
        return this.name.equals(another.name);
    }
}

此时再次运行结果如下：

返回索引2，结果正确。

循环不变量

上面线性查找法以及很多算法都涉及到一个很重要的概念叫做循环不变量，理解这个概念有助于写出正确的算法。

循环是程序设计中非常重要的一种构建逻辑的方式，近乎所有的算法都有循环这个概念。比如线性查找法只有一层for循环，每一轮循环其要做的事就是确认一下data[i]是否是目标，这个循环体里的if语句执行完以后相当于在这一轮循环中我们确认了data[i]不是目标，然后进行下一次循环。

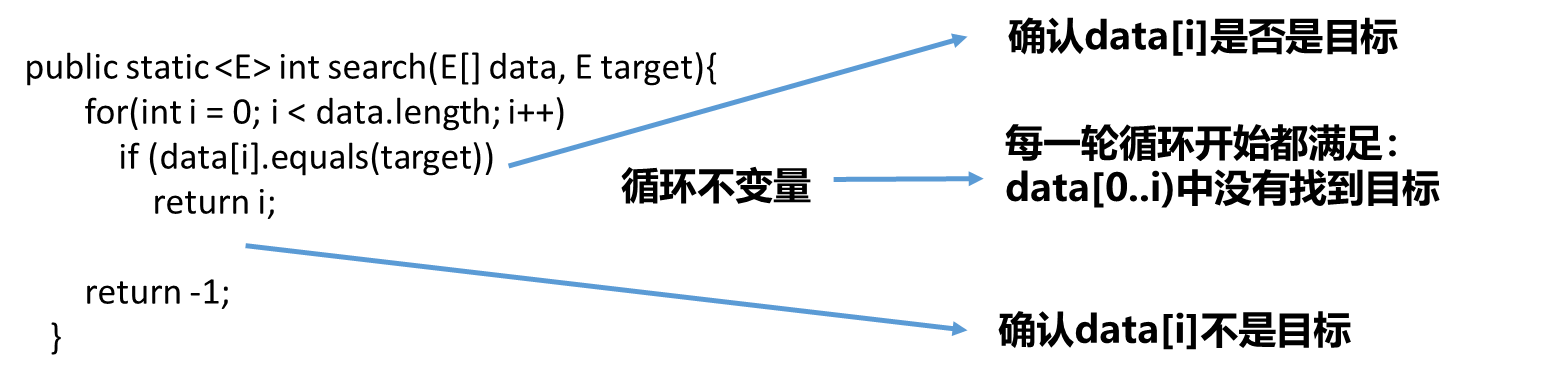
在每一轮循环开始的时候是满足一个条件data[0…i-1]中没有找到目标，这就是循环不变量。同时这个循环体的目的是在维持这个循环不变量，能够证明算法的正确性。这个算法比较简单，可能并看不来循环不变量的意义。后续一些复杂的算法设计可能更有助于看出其意义。

复杂度分析

我们要对算法做复杂度分析是因为我们要表示算法的性能。对于同一个任务，可能有不同的算法能够完成这个任务，它们的时间性能可能存在差异，我们可以采用1个测试用例或者一组测试用例对不同的算法运行实际去比较性能差异。

但是这样的比较结果很多时候是有局限性的，因为严格来讲需要运行不同算法的计算机性能是完全一致的，这是很难保证的，同时测试结果也与采用什么样的测试用例相关。更重要的这样做就必须先把算法实际实现出来才能看到它的性能，但是很多时候我们有了一个算法思想之后希望可不可能通过算法本身的思想就大致评估出这个算法的性能是优是劣，是否满足业务需求然后再来决定是否实现它。

种种原因都需要我们有一套工具能够抽象的从数学的层面就去判断一个算法的性能是怎样的，为了解决这个问题就产生了复杂度分析。

那么具体复杂度分析怎么表示算法性能呢？

以线性查找法为例：

public static <E> int search(E[] data, E target){
    for(int i = 0; i < data.length; i++)
        if (data[i].equals(target))
            return i;

    return -1;
}

从算法实现上看，这个算法执行时间的多少跟target出现在data中的位置相关，如果非常巧target就在data[0]那for循环只需执行一次，如果非常不巧target就在data末尾或者根本没有在data中出现，那么for循环需从头到尾执行。因此根据测试样例的不同这个算法实际执行的时间是不一样的。

对于上面的问题需要明确的一点是复杂度分析通常看最差的情况，不能把希望寄托在运气上每次碰巧在data前面几个元素的位置。这个思路在生活也很长使用，比如去上班要提前个10分钟以防路上堵车或者其它的事情。因此复杂度分析表示的算法运行的上界，即预估算法行性能最高就是这个样子，不可能比这个更差。

观察到线性查找法运行时间大小是和data的数组的元素数量相关的：

$$n=data.length \\ T=n?\quad T=2n? \quad T=3n? \quad T=4n? \\ \quad T=5n? \quad T=5n+2? \quad 单位:ms?$$

这个算法从头到尾扫描一遍data数组，如果将算法性能设为$T$, 那么$T=n$ 吗? 虽然自然语言是说扫描一遍data,但是仔细观察if判断里面是先要执行data[i].equals(target)返回true或false后在接着if true或 if false，这样分析那么$T=2n$ 吗？再仔细看访问data[i]是需要在data中找到第i个元素，这是一部寻址操作，这样看那么$T=3n$ 吗?再细看for循环中还要每次判断i < data.length，此时$T=4n$ 吗?再看for循环每一步还有个 i++的操作，那么$T=5n$ 吗? 最后再看循环开始是要初始化int i = 0，结尾要return i，那么$T=5n+2$ 吗?

如果还要细致分析for循环有多少指令最好方法是转换成汇编代码，但汇编代码也不够，其背后对应机器指令有多少行，而机器指令执行也不仅仅是代码有多少行的问题，它还要追溯到算法的cpu架构上，有些cpu可能对有些指令有优化，一个指令可能在另外一个cpu对应好几条指令，因此从软件开发来看，从上层分析出代码含有多少指令是一个很困难的事情，同时也是没必要的事情。即使分析出有5n+2条指令，那么这个数字对应单位是什么呢？是ms吗？每条指令执行多少时间也是和cpu架构相关的。

因此需要上面的思路进行化简，我们只需要知道算法性能和data数组规模n成一个正比关系就好了，记作：

$$O(n)$$

$O(n)$ 代表我们这个算法的性能和算法数据规模n成正比关系。因此只要分析出算法性能$T=c_1*n+c_2$ ，都可以记作$O(n)$.这个常数不重要。

复杂度描述的是随着数据规模n的增大，算法性能的变化趋势。

常见的算法复杂度

如下图所示：

• 线性查找法算法复杂度$O(n)$
• 一个数组元素组成数据对的问题，复杂度为$O(n^2)$ ，这里不是严格的n*n次，这个算法实际上是$\frac{1}{2}n^2$ 次，因为从j=i+1开始，但依然说是复杂度为$O(n^2)$ 级别，即使前面常数是一个小数也是复杂度为$O(n^2)$
• 遍历n*n二维数组就是比较严格的n*n次， 复杂度为$O(n^2)$
• 这里遍历a*a二维数组,但注意n=a*a,因此最终复杂度$O(n)$
• 数字n的二进制位数复杂度为$O(logn)$， 更严谨些是为$O(log_2n)$
• 数字n的所有约数，最笨的算法复杂度为$O(n)$ ,稍微优化一下，约数成对出现，此时为$O(\sqrt{n})$

• 长度为n的二进制数字组合，复杂度为$O(2^n)$

• 长度为n的数组的所有排列，复杂度为$O(n!)$

• 判断数字n是否为偶数，复杂度为$O(1)$ ,return n%2==0

总体来看：

$$O(1)<O(logn)<O(\sqrt{n})<O(n)<O(nlogn)<O(n^2)<O(2^n)<O(n!)$$

空间复杂度同理时间复杂度。

测试算法性能

考虑测试算法性能的数据规模通常采用十万百万级别的，首先写一个生成测试样例的ArrayGenerator类:

public class ArrayGenerator {
    private ArrayGenerator() {}

    public static Integer[] generateOrderedArray(int n) {
        Integer[] arr = new Integer[n];
        for (int i = 0; i < n; i++) {
            arr[i] = i;
        }
        return arr;
    }
}

测试代码：

public class LinearSearch {

    private LinearSearch(){}

    public static <E> int search(E[] data, E target){

        for(int i = 0; i < data.length; i ++)
            if(data[i].equals(target))
                return i;

        return -1;
    }

    public static void main(String[] args){

        int[] dataSize = {1000000, 10000000};
        for(int n: dataSize) {
            Integer[] data = ArrayGenerator.generateOrderedArray(n);

            long startTime = System.nanoTime();
            for (int k = 0; k < 100; k++)
                LinearSearch.search(data, n);
            long endTime = System.nanoTime();

            double time = (endTime - startTime) / 1000000000.0;
            System.out.println("n = " + n + ", 100 runs : " + time + "s");
        }
    }
}

可以发现n为1千万的用时大概是n为1百万用时的10倍.侧面反映出线性查找法时间复杂度是$O(n)$ 级别的，随着n线性增长的。