Selection Sort

最简单的排序算法：选择排序

排序算法是计算机科学领域研究的非常深入的一类算法，排序算法的作用是让数据有序，同时排序这个动作本身非常重要，很多时候面对无序的数据都需要先对其进行一次排序，然后再进行处理就会简单方便很多。排序算法种类很多，适用于不同的情境，同时不同的排序算法也能反映出算法设计的不同思想。

什么是选择排序法？其本身的思路非常简单，比如有一系列待排序的元素，怎么把这些乱序的元素从小到大排列好呢？我们可能很自然的思路就是把这一堆元素中最小的先拿出来，然后从剩下的元素中再把最小的拿出来，再把剩下的元素中最小的拿出来…每次选择还没处理的元素里最小的元素。这样的思路就是选择排序法。

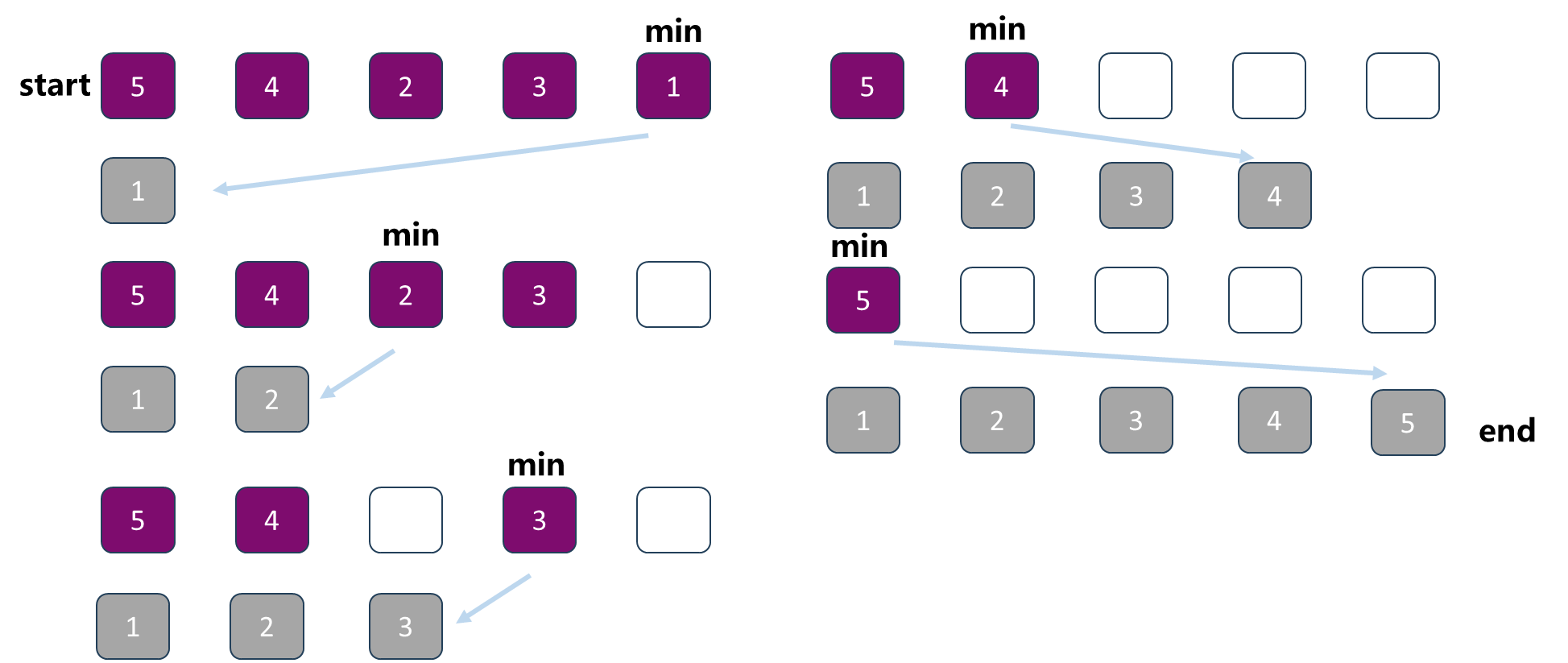
以下面图中的一个数组选择排序为例：

image-20251028124841427

每一次找出最小值取出来，最终从54231一个乱序数组排成了一个有序数组12345.

但上图的演示其实反映出了选择排序的一个问题，从原始的无序数组54231到最终的有序数组12345这个过程其实使用了一个额外的空间.需要新开辟一个数组来存储每轮种选出的最小值，即排序过程占用了额外的空间，造成了空间的浪费。

那么这样选择排序的思路可否做到原地完成？

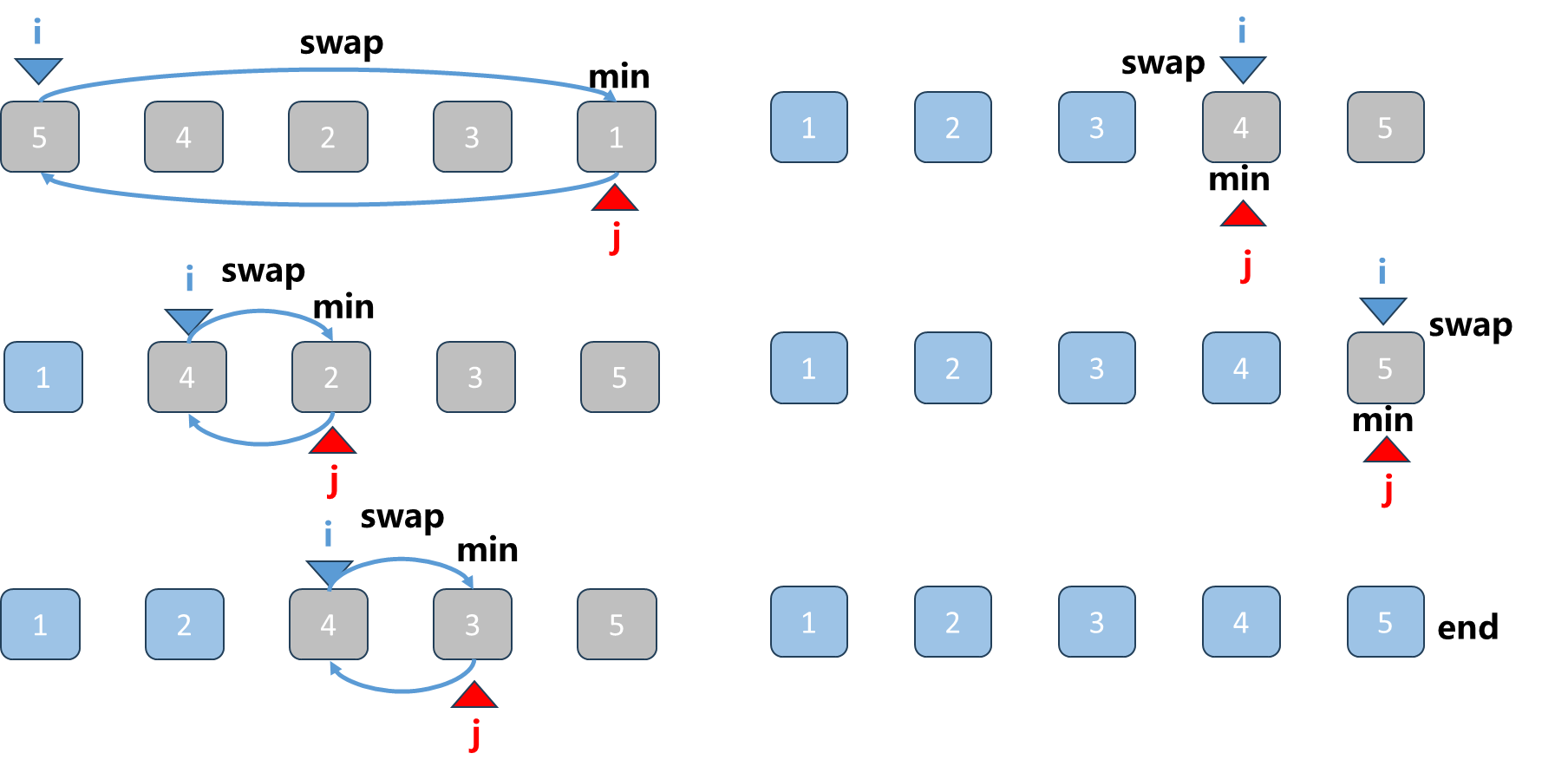
image-20251028135844625

如上图所示，可以用一个蓝色索引i指向每轮循环时开头的位置，红色索引j指向每轮中的最小元素的位置。每一轮，将两个索引指向的元素进行交换，然后将蓝色索引i++, 最终即可完成原地选择排序。

这个处理过程中的循环不变量：

  • 每一步的时候arr[i…n）未排序
  • 相当于arr[0,i）已排序
  • 然后将arr[i…n)中的最小值放到arr[i]的位置。

实现选择排序

java实现如下：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
public class Selection_Sort {
    private Selection_Sort(){}

    public static void sort(int[] data){
		// 这里实现的是原地交换的 选择排序算法
        for (int i = 0; i< data.length; i++){

            int min_index = i;
            for(int j = i ; j< data.length;j++)
                if(data[j] < data[min_index])
                    min_index = j;

            swap(data, i, min_index);
        }

    }

    private static void swap(int[] data, int i, int j){
        int temp = data[i];
        data[i] = data[j];
        data[j] = temp;
    }

    public  static void main(String[] args){
        int[] data = {5,4,2,3,1};
        Selection_Sort.sort(data);
        for(int e:data)
            System.out.print(e+" ");
        
    }
}

image-20251028142629864

最终排序结果为1 2 3 4 5，算法逻辑正确。

泛型

与上篇实现线性查找法一样，上面实现依旧有一个问题，那就是只对int类型的数组有效。我们希望算法对所有数据类型都支持，因此需要采用==泛型机制==。

泛型实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public class Selection_Sort {

    private Selection_Sort(){}

    public static <E extends Comparable<E>> void sort(E[] arr){

        // arr[0...i) 是有序的；arr[i...n) 是无序的
        for(int i = 0; i < arr.length; i ++){

            // 选择 arr[i...n) 中的最小值
            int minIndex = i;
            for(int j = i; j < arr.length; j ++){
                if(arr[j].compareTo(arr[minIndex]) < 0)
                    minIndex = j;
            }

            swap(arr, i, minIndex);
        }
    }

    private static <E> void swap(E[] arr, int i, int j){

        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args){

        Integer[] arr = {1, 4, 2, 3, 6, 5};
        Selection_Sort.sort(arr);
        for(int e: arr)
            System.out.print(e + " ");
        System.out.println();
    }
}

几个代码细节：

1
2
3
4
public static <E extends Comparable<E>> void sort(E[] arr)
if(arr[j].compareTo(arr[minIndex]) < 0)
private static <E> void swap(E[] arr, int i, int j){
E t = arr[i];

Java 是强类型语言，排序算法必须确保传入的元素可比较。 因此第一行代码通过 <E extends Comparable<E>> 限制类型。

第一行代码 中<E extends Comparable<E>> 表示类型参数 E 必须实现了 Comparable 接口，也就是说这些元素可以通过 compareTo() 方法相互比较。

第二行代码通过 if (arr[j].compareTo(arr[minIndex]) < 0) 来判断哪个元素更小，而不是像基本类型那样直接用 < 比较。这样，sort() 方法就可以同时排序 Integer、String、Double 等任意可比较对象。
第三行代码这里的 swap 方法不需要比较，只需要交换两个元素的位置。所以泛型只写 <E>，不用加 extends Comparable<E> 约束。

使用自定义Student类进行测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
public class Student implements Comparable<Student>{

    private String name;
    private int score;

    public Student(String name, int score){
        this.name = name;
        this.score = score;
    }

    @Override
    public int compareTo(Student another){
        // 如何比较由自己来定义决定

//        if(this.score < another.score)
//            return -1;
//        else if(this.score == another.score)
//            return 0;
//        return 1;

//        return this.score - another.score;
        return another.score - this.score;  
    }

    @Override
    public boolean equals(Object student){

        if(this == student)
            return true;

        if(student == null)
            return false;

        if(this.getClass() != student.getClass())
            return false;

        Student another = (Student)student;
        return this.score == another.score;
    }

    @Override
    public String toString(){
        return String.format("Student(name: %s, score: %d)", name, score);
    }
}

  • Comparable 是 Java 提供的一个比较接口，用于定义对象之间的自然排序规则。当一个类实现了 Comparable<T> 接口，就必须重写 compareTo() 方法，这样该类的对象就能被排序。

  • compareTo(Student another) 方法这是比较的核心逻辑，由自己定义实现。 它返回一个 整数值：

    • 返回 负数：表示当前对象 this 比参数对象 another 小
    • 返回 0：表示相等
    • 返回 正数：表示当前对象比参数对象大

    在代码中：

    1
    return another.score - this.score;

    意味着按照分数从高到低排序（分高的排前面）。
    如果想要升序排序（分低的排前），可以写成：

    1
    return this.score - another.score;

    注意：compareTo() 的定义非常灵活，完全由你决定怎么比较。也可以根据名字、年龄、成绩等决定排序规则。

  • toString() 用来定义对象在被打印或输出时的显示方式

测试：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
public class Selection_Sort {

    private Selection_Sort(){}

    public static <E extends Comparable<E>> void sort(E[] arr){

        // arr[0...i) 是有序的；arr[i...n) 是无序的
        for(int i = 0; i < arr.length; i ++){

            // 选择 arr[i...n) 中的最小值
            int minIndex = i;
            for(int j = i; j < arr.length; j ++){
                if(arr[j].compareTo(arr[minIndex]) < 0)
                    minIndex = j;
            }

            swap(arr, i, minIndex);
        }
    }

    private static <E> void swap(E[] arr, int i, int j){

        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args){

        Integer[] arr = {1, 4, 2, 3, 6, 5};
        Selection_Sort.sort(arr);
        for(int e: arr)
            System.out.print(e + " ");
        System.out.println();

        Student[] students = {
              new  Student("A", 80),
                new  Student("B", 60),
                new  Student("C", 70),
                new  Student("D", 100),
        };
        Selection_Sort.sort(students);

        for(Student s: students){
            System.out.print(s + " ");
        }

    }
}

image-20251028160045748

可以发现最终结果按照从大到小(怎么比较看具体compareTo如何实现)的顺序排序，学生D分数最高为100分.

复杂度分析

首先选择排序代码的核心逻辑如下：

1
2
3
4
5
6
7
8
9
10
11
for(int i = 0; i < arr.length; i ++){

    // 选择 arr[i...n) 中的最小值
    int minIndex = i;
    for(int j = i; j < arr.length; j ++){
        if(arr[j].compareTo(arr[minIndex]) < 0)
            minIndex = j;
    }

    swap(arr, i, minIndex);
}

可以发现当i=0 时，第二重循环运行n 次；当i=1 时，第二重循环运行n-1 次；当i=2 时，第二重循环运行n-2 次；然后这样一直循环下去。整体来说二重循环运行次数：

1+2+3+...+n=n∗(n+1)2=12n2+12nO(n2)1+2+3+...+n=\frac{n*(n+1)}{2}=\frac{1}{2}n^2+\frac{1}{2}n\\ \\ O(n^2)

因此选择排序法的时间复杂度为O(n2)O(n^2) 级别.

接下来用代码测试选择排序算法的性能：

  • 因为要排序，所以测试用例要是乱序的，因此对上篇的ArrayGenerator添加乱序数组生成方法
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
import java.util.Random;

public class ArrayGenerator {

    private ArrayGenerator(){}

    public static Integer[] generateOrderedArray(int n){

        Integer[] arr = new Integer[n];
        for(int i = 0; i < n; i ++)
            arr[i] = i;
        return arr;
    }

    // 生成一个长度为 n 的随机数组，每个数字的范围是 [0, bound)
    public static Integer[] generateRandomArray(int n, int bound){

        Integer[] arr = new Integer[n];
        Random rnd = new Random();
        for(int i = 0; i < n; i ++)
            arr[i] = rnd.nextInt(bound);
        return arr;
    }
}
  • 实现一个SortingHelper类 来测试排序算法的性能与正确性
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
public class SortingHelper {

    private SortingHelper(){}

    public static <E extends Comparable<E>> boolean isSorted(E[] arr){

        for(int i = 1; i < arr.length; i ++)
            if(arr[i - 1].compareTo(arr[i]) > 0)
                return false;
        return true;
    }

    public static <E extends Comparable<E>> void sortTest(String sortname, E[] arr){

        long startTime = System.nanoTime();
        if(sortname.equals("SelectionSort"))
            Selection_Sort.sort(arr);
        long endTime = System.nanoTime();

        double time = (endTime - startTime) / 1000000000.0;

        if(!SortingHelper.isSorted(arr))
            throw new RuntimeException(sortname + " failed");
        System.out.println(String.format("%s , n = %d : %f s", sortname, arr.length, time));
    }
}

上面代码包含两个静态泛型方法。首先isSorted(E[] arr) 用于判断一个数组是否已经按升序排好序：通过遍历数组，如果发现前一个元素比后一个大（compareTo()>0），说明排序错误，返回 false，否则返回 true。其次，sortTest(String sortname, E[] arr) 用于计时并验证排序算法。它记录排序前后的纳秒时间差计算运行耗时，并根据传入的算法名调用相应的排序方法（这里是 Selection_Sort.sort()）。排序完成后，它调用 isSorted() 检查结果是否正确，若未排序好则抛出异常，否则打印算法名、数组长度与耗时。

  • 测试代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
public class Selection_Sort {

    private Selection_Sort(){}

    public static <E extends Comparable<E>> void sort(E[] arr){

        // arr[0...i) 是有序的；arr[i...n) 是无序的
        for(int i = 0; i < arr.length; i ++){

            // 选择 arr[i...n) 中的最小值
            int minIndex = i;
            for(int j = i; j < arr.length; j ++){
                if(arr[j].compareTo(arr[minIndex]) < 0)
                    minIndex = j;
            }

            swap(arr, i, minIndex);
        }
    }

    private static <E> void swap(E[] arr, int i, int j){

        E t = arr[i];
        arr[i] = arr[j];
        arr[j] = t;
    }

    public static void main(String[] args){

        int[] dataSize = {10000, 100000};
        for(int n: dataSize){
            Integer[] arr = ArrayGenerator.generateRandomArray(n, n);
            SortingHelper.sortTest("SelectionSort", arr);
        }


    }
}

image-20251028163648616

最终结果如上，当n=10000时，一共用时0.116s；当n=100000时，一共用时11.03s. 可见 n扩大了10倍，但是耗时扩大了100倍，这里也反映处了选择排序算法的时间复杂度是O(n2)O(n^2) 级别的。