Stack

什么是栈

栈也是一种线性的数据结构. 相比于数组，栈相应的操作更少，栈对应的操作是上篇数组设计的操作中的子集.为什么这么说呢？相对于栈这种数据结构而言，可以本质理解它就是一个数组，把数据排开来放，但是只能从一端添加元素，也只能从同一端取出元素，这一端通常也称为栈顶.

通过这样的条件限定数组形成了栈这种数据结构，它可以在计算机世界中对于组建逻辑有着非常重要的作用.

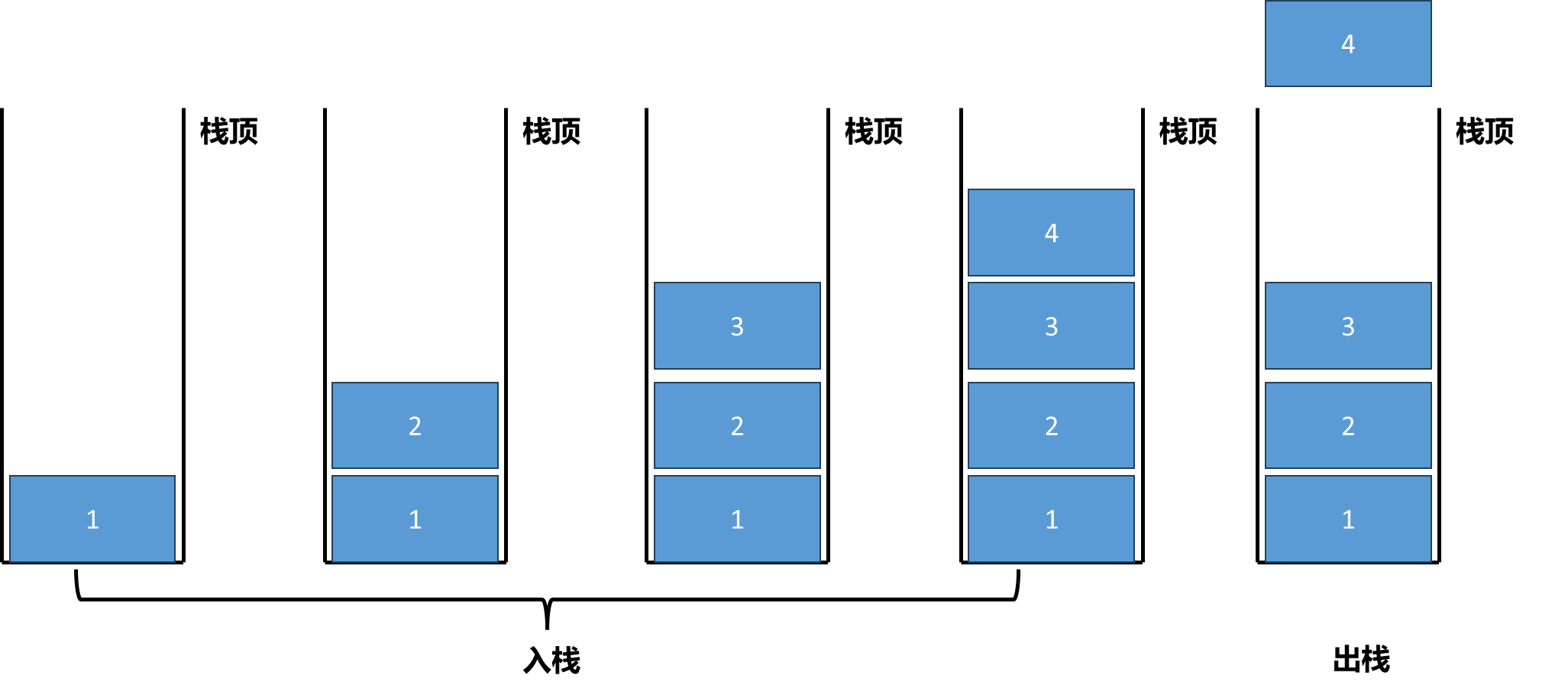
image-20251102211700506

如上面图示过程，向栈中添加数据只能从一端添加元素，这个过程通常称为入栈. 入栈过程中元素2只能放在元素1的上面，元素3只能放在元素2 的上面，元素4只能放在元素1的上面. 此时如果想从栈中取出数据，我们只能取出元素4，因为元素4在栈顶，我们取不到元素3、元素2、元素1，甚至从用户的角度根本看不到3、2、1这些数据. 而将栈顶元素4取出的这个过程叫做出栈.

可以发现：

  • 栈是一种后进先出的数据结构
  • Last In First Out(LIFO)

这样一种数据结构在计算的世界里拥有着不可思议的作用.

栈的两个相关应用：

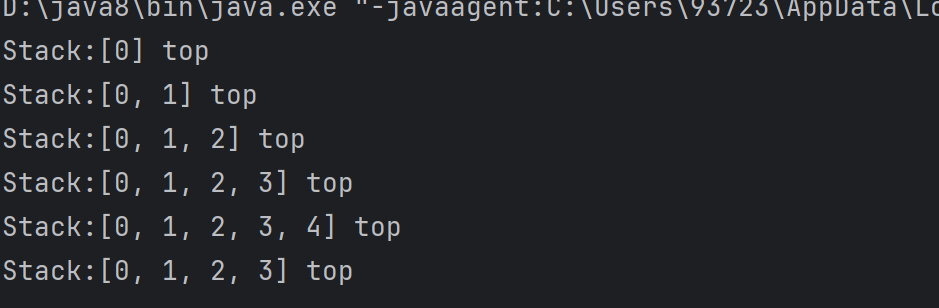
  • 我们使用的编辑器比如word或者其它IDE里面都会有一个叫做undo(撤销)的操作，我们应该都会经常使用到这个功能，编辑器背后undo操作的原理就是靠一个栈来进行维护的. 就像上面图中如果你输入了数字 1 2 3 4，相当于将这四个数字压入栈中，你点撤销功能或者 Ctrl+Z此时就会从栈顶拿出元素，此时数字4就会被删掉相当于出栈.
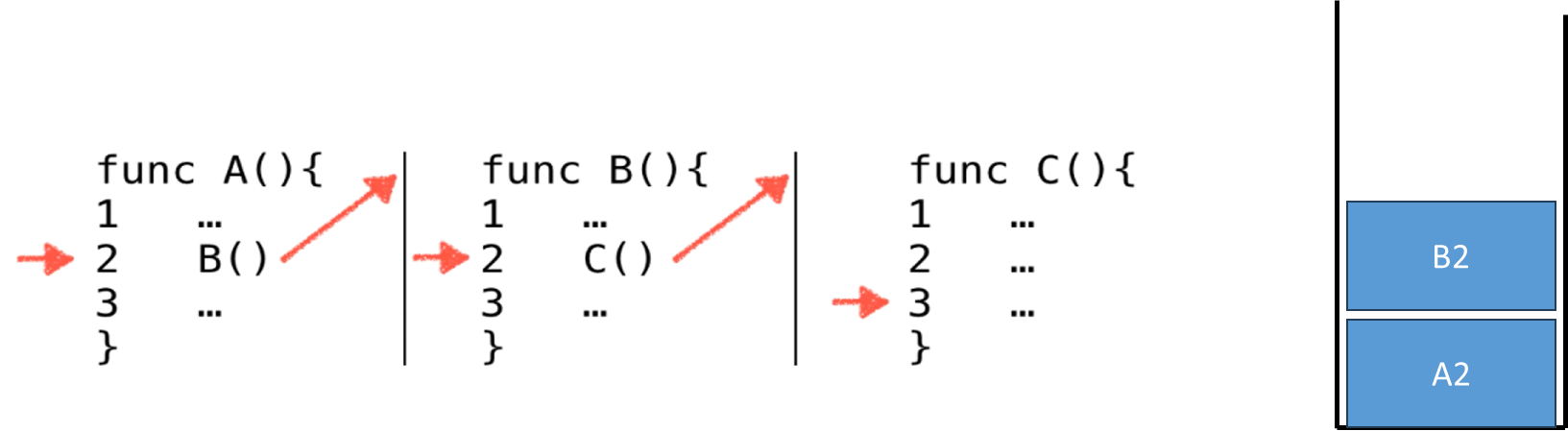
  • 程序调用的系统栈. 如下图所示，在程序调用的过程中通常会出现在一个逻辑的中间先终止然后跳到另外一个逻辑去执行，所谓的子函数调用这个过程.这个过程中计算机就需要使用一个称为系统栈的本质就是栈的数据结构来记录程序的调用过程. 就像下图的三个函数A、B、C，对于A这个函数执行到一半需要调用子函数B，对于B这个函数执行到一般要调用子函数C,对于C这个子函数它就直接执行完了,不需要调用子函数. 我们开始执行A时到第二行时要跳转到B，暂时中断A，此时系统栈就会记录一个信息A2,接着执行B到第二行要跳转C,此时系统栈就会记录一个信息B. 此时执行C执行完了，执行完之后计算机接下来执行谁呢？此时需要看一下系统栈了，栈顶是B2,那么计算机就得知刚刚是执行B函数的第二行中断了，此时跳回B2行，B2也会出栈.B函数执行完此时看栈顶为A2,接着A2出栈，跳回A2行执行完A.整个过程结束.

image-20251102213546882

栈的基本实现

栈这种数据结构虽然非常有用，但是非常简单的。基本上只涉及5个操作：

  • void push(E) 入栈 O(1)
  • E pop() 出栈 O(1)
  • E peek() 看栈顶元素 O(1)
  • int getSize() 栈的元素数量 O(1)
  • boolean is Empty() 栈是否非空 O(1)

在上篇动态数组的基础上实现栈：

  • 实现一个接口
1
2
3
4
5
6
7
8
9
public interface Stack <E>{

    int getSize();
    boolean isEmpty();
    void push(E e);
    E pop();
    E peek();
}

  • 在动态数组基础上实现ArrayStack类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
public class ArrayStack <E> implements  Stack<E> {

    Array<E>  array;

    public ArrayStack(int capacity){
        array = new Array<>(capacity);

    }

    public ArrayStack(){
        array = new Array<>();
    }

    @Override
    public int getSize(){
        return array.getSize();
    }

    @Override
    public boolean isEmpty(){
        return array.isEmpty();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    public void push(E e){
        array.addLast(e);
    }

    @Override
    public E pop(){
        array.removeLast();
    }

    @Override
    public E peek(){
        return array.getLast();
    }

    @Override
    public String toString(){
        StringBuilder sb = new StringBuilder();
        sb.append("Stack:");
        sb.append("[");
        for(int i = 0; i < array.getSize(); i++){
            sb.append(array.get(i));
            if(i != array.getSize() - 1){
                sb.append(", ");
            }
        }
        sb.append("] top");

        return  sb.toString();
    }

}

测试代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
public class Main {

    public static void main(String[] args) {

        ArrayStack<Integer>   stack = new ArrayStack<>();

        for(int i=0;i<5;i++){
            stack.push(i);
            System.out.println(stack);
        }
        stack.pop();
        System.out.println(stack);
    }
}

image-20251106011516595

可见上面动态数组的基础上实现栈非常简单.

括号匹配

栈的另一个应用就是括号匹配. 我们编程时写表达式需要用到小括号(), 写数组时用到中括号[]，写for循环需要用到大括号{},经常会遇到括号套括号的情况， 这种情况下会产生一个括号匹配的问题. 如果括号匹配不成功，编译器就会报错，那么编译器是如何检查括号匹配的问题呢？其实使用的就是一个栈.

以LeetCode中题号20名为”Valid Parentheses“题目举例：

20.Valid Parentheses

Given a string s containing just the characters '(', ')', '{', '}', '[' and ']', determine if the input string is valid.

An input string is valid if:

  1. Open brackets must be closed by the same type of brackets.（左括号必须由相同类型的右括号闭合)
  2. Open brackets must be closed in the correct order.（左括号必须按照正确的顺序闭合）
  3. Every close bracket has a corresponding open bracket of the same type.（每个右括号必须有个对应类型的左括号与之匹配）

Examples:

Input: s = “()” Output: true

Input: s = “()[]{}” Output: true

Input: s = “(]” Output: false

Input: s = “([])” Output: true

Input: s = “([)]” Output: false

Constraints:

  • 1 <= s.length <= 104
  • s consists of parentheses only '()[]{}'.

题解：

  • 先分析一下用栈解决时True的情况

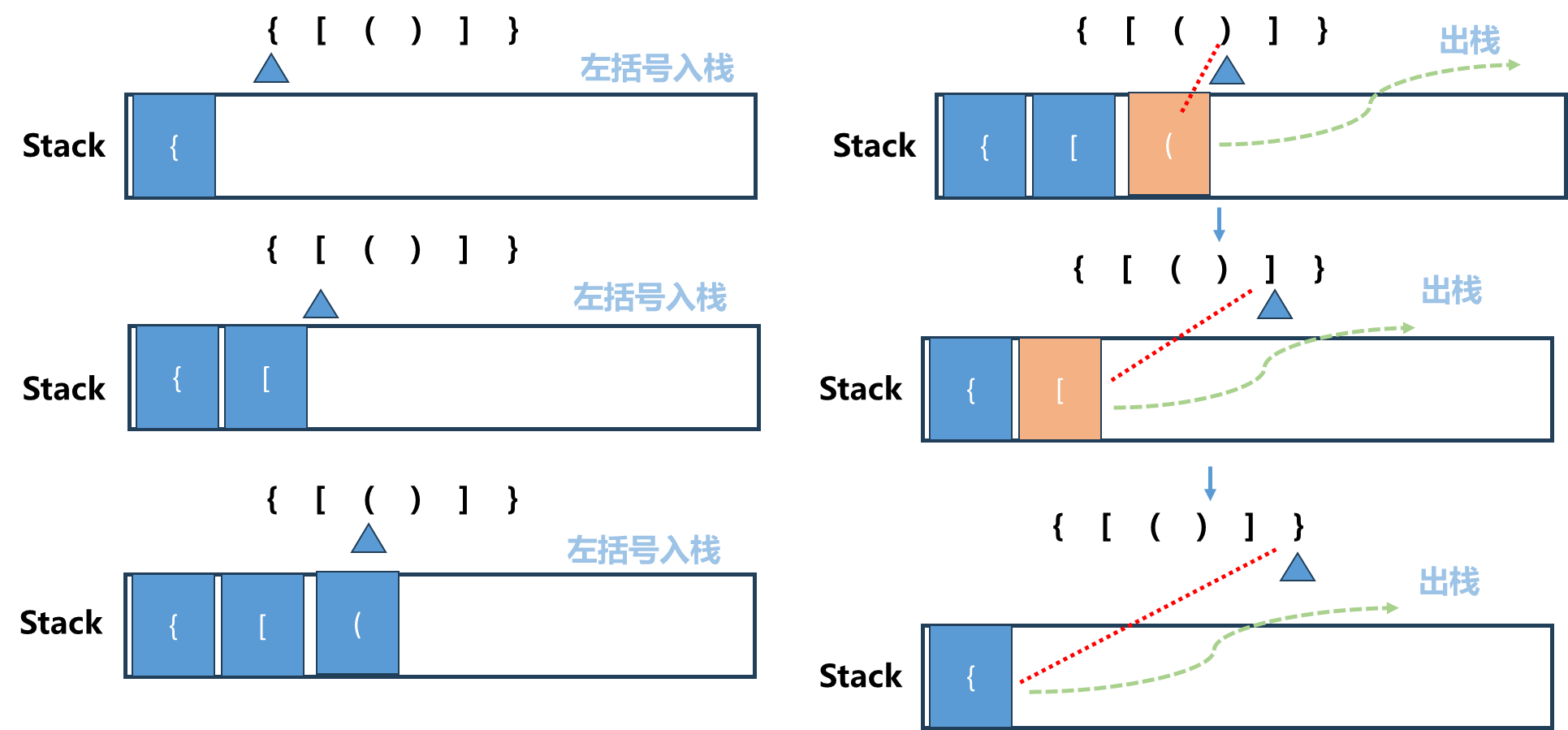
image-20251108142605191

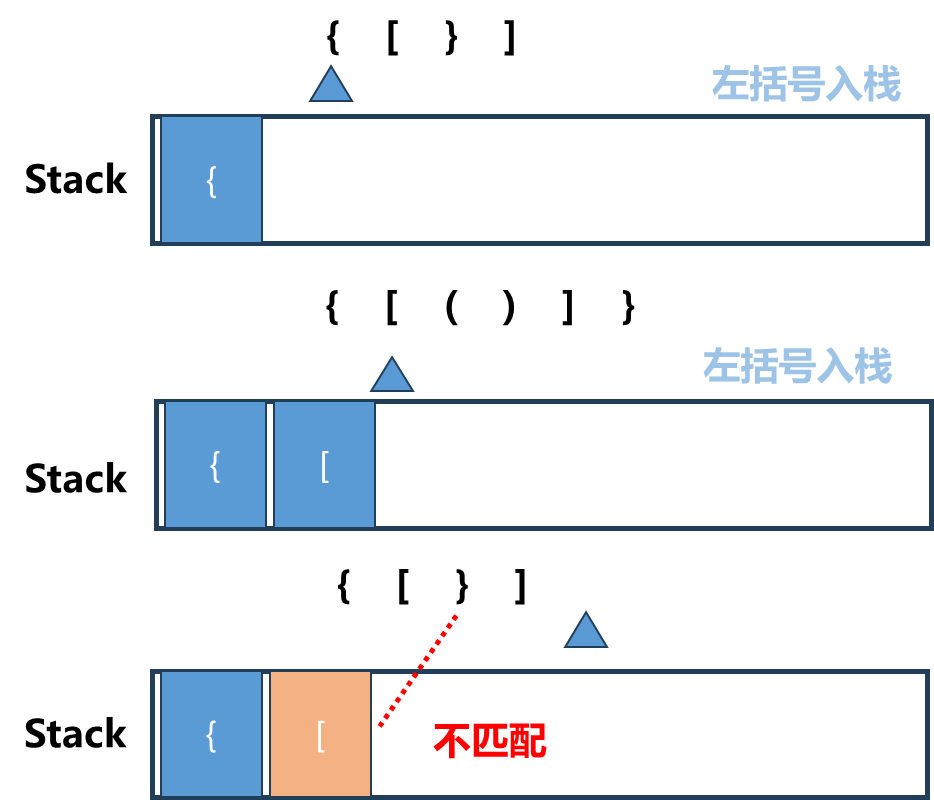
如上图所示，假设输入是”{[()]}“，我们遍历这个字符串，如果此时为左括号，那么就入栈（对应图中左边一列）.如果此时为右括号，我们就将此时的右括号与栈顶的左括号匹配，匹配成功则将栈顶的左括号出栈，进行下一步匹配. 最终栈元素为空，说明全部匹配成功!

  • False的情况
image-20251108145734093

如上图所示，假设输入是”{[}}“，我们遍历这个字符串，如果此时为左括号，同样执行入栈操作.如果此时为右括号，我们就将此时的右括号与栈顶的左括号匹配，此时可以发现不匹配，直接输出False.

栈顶元素反映了在嵌套的层次关系中，最近的需要匹配的元素.

编程实现：

  • 使用java封装的Stack类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
import java.util.Stack;

class Solution {
    public boolean isValid(String s) {
        
        Stack<Character> stack = new Stack<>();
        for(int i=0;i <s.length();i++){
            char c = s.charAt(i);
            if(c == '{' || c=='(' || c=='[')
                stack.push(c);
            else{
                if(stack.isEmpty())
                    return false;
                char topChar = stack.pop();
                if(c ==')'&& topChar !='(')
                    return false;
                if(c ==']'&& topChar !='[')
                    return false;
                if(c =='}'&& topChar !='{')
                    return false;
            }
        }
        return stack.isEmpty();
    }
}
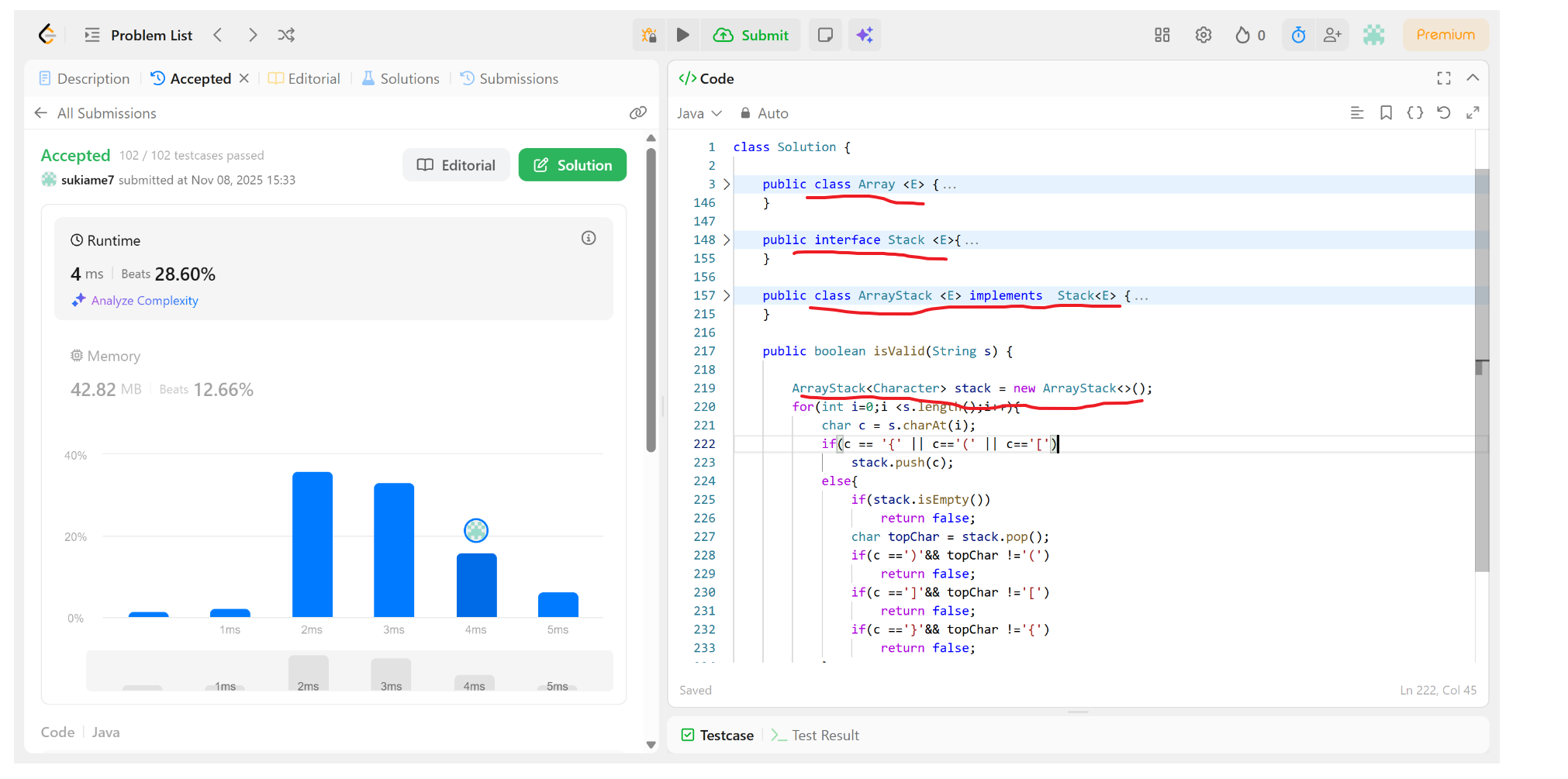
  • 使用上面我们自己实现的ArrayStack类，因为LeetCode只能提交一个类，所以需将Array类、interface接口类、ArrayStack类都放进来写成一个内部类，代码看着可能过长，但这三个类定义都是前面写过的，直接copy进来即可.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
class Solution {

    public class Array <E> {
        private E[]  data;
        private int size;

        // 构造函数， 传入数组的容量capacity构造Array
        public Array(int capacity) {
            data = (E[])new Object[capacity];
            size = 0;
        }

        // 无参数构造函数，默认 数组的容量capacity=10
        public Array() {
            this(10);
        }

        public int getSize() {
            return size;
        }

        public int getCapacity() {
            return data.length;
        }

        public boolean isEmpty() {
            return size == 0;
        }

        public void addLast(E e){
            add(size,e);
        }

        public void addFirst(E e){
            add(0,e);
        }
        public void add(int index, E e){

            if(index < 0 || index > size){
                throw new RuntimeException("Index out of bounds");
            }

            if(size == data.length){
                resize(2 * data.length);
            }
            for(int i = size-1; i >= index; i--){
                data[i+1] = data[i];
            }
            data[index] = e;
            size++;
        }

        public E get(int index){
            if(index < 0 || index >= size){
                throw new RuntimeException("Index out of bounds");
            }

            return data[index];
        }


        public E getLast(){
            return get(size-1);
        }

        public E getFirst(){
            return get(0);
        }

        public void set(int index, E e){
            if(index < 0 || index >= size){
                throw new RuntimeException("Index out of bounds");
            }
            data[index] = e;
        }

        public boolean contains(E e){
            for(int i = 0; i < size; i++){
                if(data[i] .equals(e) )
                    return true;
            }
            return false;
        }

        public int find(E e){
            for(int i = 0; i < size; i++){
                if(data[i] .equals(e) )
                    return i;
            }
            return -1;
        }

        public E remove(int index){
            if(index < 0 || index >= size){
                throw new RuntimeException("Index out of bounds");
            }
            E removed = data[index];
            for(int i=index+1; i < size; i++){
                data[i-1] = data[i];
            }
            size--;
            data[size] = null;

            if(size == data.length/2){
                resize(data.length/2);
            }
            return removed;
        }

        public  E removeFirst(){
            return remove(0);
        }

        public E removeLast(){
            return remove(size-1);
        }

        public void removeElement(E e){
            int index = find(e);
            if(index != -1){
                remove(index);
            }
        }
        @Override
        public String toString() {
            StringBuilder res = new StringBuilder();
            res.append(String.format("Array: size = %d, capacity = %d\n", size, data.length));
            res.append("[");
            for (int i = 0; i < size; i++) {
                res.append(data[i]);
                if(i != size - 1){
                    res.append(", ");
                }
            }
            res.append("]");
            return res.toString();
        }

        private void  resize(int newCapacity){
            E[] newData = (E[])new Object[newCapacity];
            for(int i = 0; i < size; i++){
                newData[i] = data[i];
            }
            data = newData;
        }
    }

    public interface Stack <E>{

        int getSize();
        boolean isEmpty();
        void push(E e);
        E pop();
        E peek();
    }

    public class ArrayStack <E> implements  Stack<E> {

        Array<E>  array;

        public ArrayStack(int capacity){
            array = new Array<>(capacity);

        }

        public ArrayStack(){
            array = new Array<>();
        }

        @Override
        public int getSize(){
            return array.getSize();
        }

        @Override
        public boolean isEmpty(){
            return array.isEmpty();
        }

        public int getCapacity(){
            return array.getCapacity();
        }

        @Override
        public void push(E e){
            array.addLast(e);
        }

        @Override
        public E pop(){
            return array.removeLast();
        }

        @Override
        public E peek(){
            return array.getLast();
        }

        @Override
        public String toString(){
            StringBuilder sb = new StringBuilder();
            sb.append("Stack:");
            sb.append("[");
            for(int i = 0; i < array.getSize(); i++){
                sb.append(array.get(i));
                if(i != array.getSize() - 1){
                    sb.append(", ");
                }
            }
            sb.append("] top");

            return  sb.toString();
        }

    }

    public boolean isValid(String s) {
        
        ArrayStack<Character> stack = new ArrayStack<>();
        for(int i=0;i <s.length();i++){
            char c = s.charAt(i);
            if(c == '{' || c=='(' || c=='[')
                stack.push(c);
            else{
                if(stack.isEmpty())
                    return false;
                char topChar = stack.pop();
                if(c ==')'&& topChar !='(')
                    return false;
                if(c ==']'&& topChar !='[')
                    return false;
                if(c =='}'&& topChar !='{')
                    return false;
            }
        }
        return stack.isEmpty();
    }
}

image-20251108153648078

结果如上图，成功AC!我们只需把前面写好的类定义放进来，把Stack定义换成我们自己实现的ArrayStack即可.

附c++写法：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
class Solution {
public:
    bool isValid(string s) {
        
        const int N = 1e4+10;
        char stack[N], c;
        int tt=0;

        for(char c:s)
        {
            if (c == '"') continue;
            if(c=='{' || c=='(' || c=='[')
                stack[++tt] = c;
            else{
                if(tt==0)
                    return false;
                char top = stack[tt--];
                if(c==']' && top!='[')
                    return false;
                if(c==')' && top!='(')
                    return false;
                if(c=='}' && top!='{')
                    return false;

            }
        }
        return tt==0;
    }
};

Queue

什么是队列

队列(Queue) 本身也是一种线性数据结构，同栈一样，队列的操作也是数组的子集.和栈不同的是，队列只能从一端(队尾)添加元素，只能从另一端(队首)取出元素。

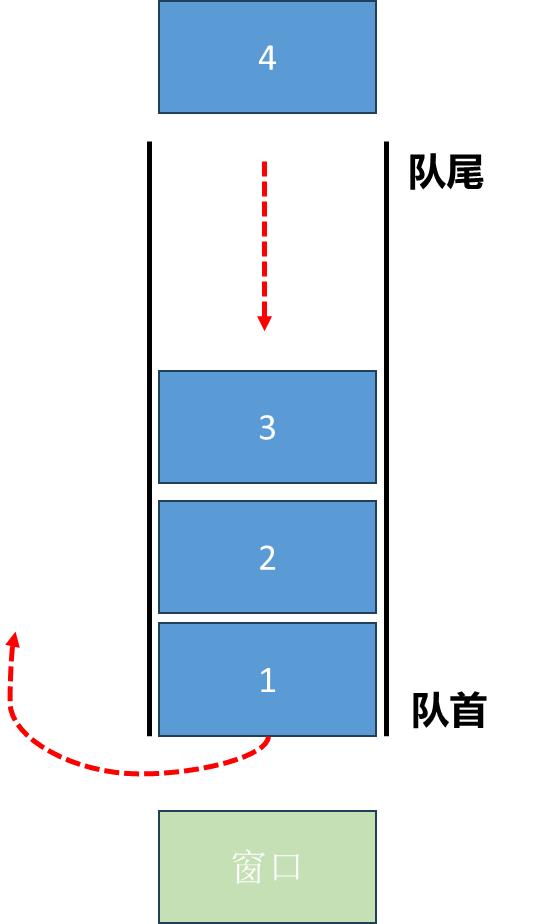
队列这个名称由来也与我们生活中排队那个队列是一致的。以下图为例，假如我们去食堂窗口打饭排队，每新来一个人比如图中的4就从队尾进去，而队首的第一个人如图中1打完饭就从队首出去.

image-20251108204345811

可以发现：

  • 队列是一种先进先出的数据结构(先到先得)
  • First In First Out(FIFO)

队列的基本实现

队列要实现的主要方法与栈类似，主要涉及下面几类：

Queue

  • void enqueue(E) 入队：向队列添加一个元素 O(1)
  • E dequeue() 出队：从队列取出一个元素 **O(n) ** 注意！！
  • E getFront() 查看队首元素 O(1)
  • int getSize() 队列元素数量 O(1)
  • boolean isEmpty() 判断队列是否为空 O(1)

同样在动态数组的基础上实现队列：

  • 实现一个接口
1
2
3
4
5
6
7
public interface Queue <E>{
    int getSize();
    boolean isEmpty();
    void enqueue(E e);
    E dequeue();
    E getFront();
}
  • 在动态数组基础上实现ArrayQueue类
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
public class ArrayQueue <E> implements Queue<E>{
    private Array<E> array;

    public ArrayQueue(int capacity){
        array = new Array<>(capacity);
    }
    public ArrayQueue(){
        array = new Array<>();
    }

    @Override
    public int getSize()
    {
        return array.getSize();
    }

    @Override
    public boolean isEmpty(){
        return array.isEmpty();
    }

    public int getCapacity(){
        return array.getCapacity();
    }

    @Override
    public void enqueue(E e){
        array.addLast(e);
    }

    @Override
    public E dequeue(){
        return array.removeFirst();
    }

    @Override
    public E getFront(){
        return array.getFirst();
    }

    @Override
    public String toString() {

        StringBuilder res = new StringBuilder();
        res.append("Queue: ");
        res.append("front [");
        for (int i = 0; i < array.getSize() ; i++) {
            res.append(array.get(i));
            if(i != array.getSize() - 1){
                res.append(", ");
            }
        }
        res.append("] tail");
        return res.toString();
    }

    public  static void main(String[] args){
        ArrayQueue<Integer> queue = new ArrayQueue<>();
        for  (int i = 0; i < 6; i++) {
            queue.enqueue(i);
            System.out.println(queue);

            if(i%3 ==2){
                queue.dequeue();
                System.out.println(queue);
            }

        }

    }
}

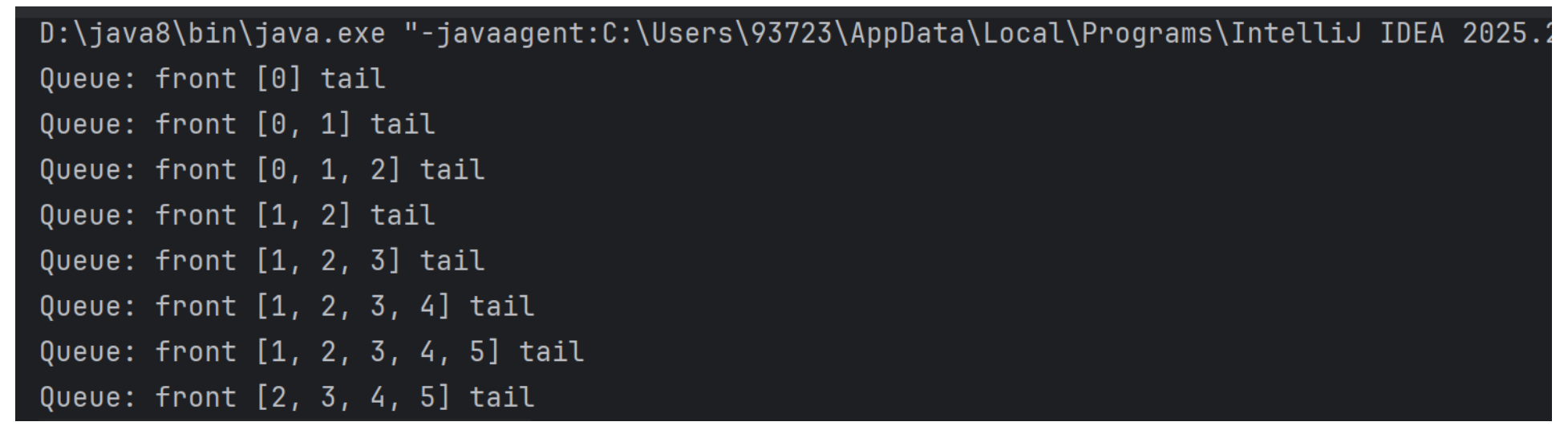
image-20251108215326751

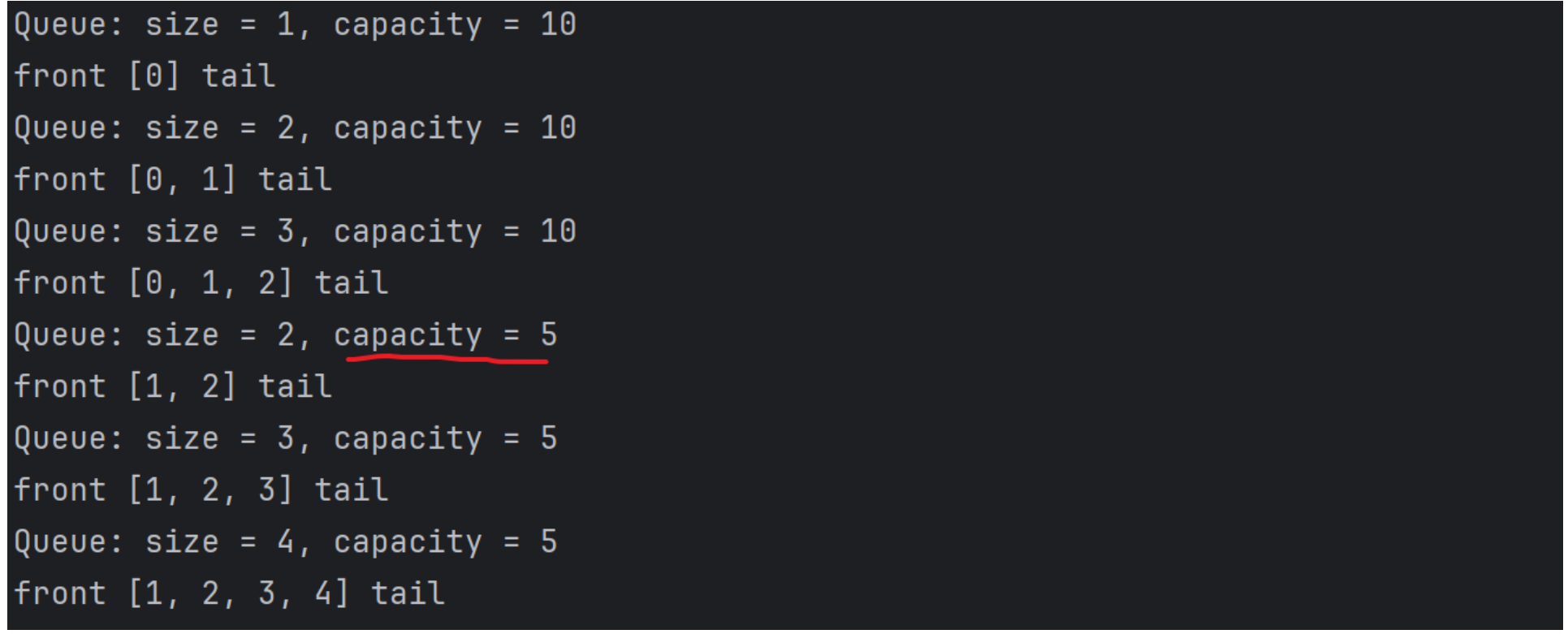
测试结果如上，每添加三个元素就从队首取出一元素，打印正确！

队列的四种操作复杂度都是O(n), 而另一种getFront()方法即从队首取出元素复杂度为O(n)，因为拿出第一个元素，数组后面的元素都要往前挪一步，对应前面动态数组RemoveFrist()方法的逻辑. 如果数组元素很多比如100w,那么每次出队都要有100W次操作，时间消耗过大，那么如何改进呢？

循环队列

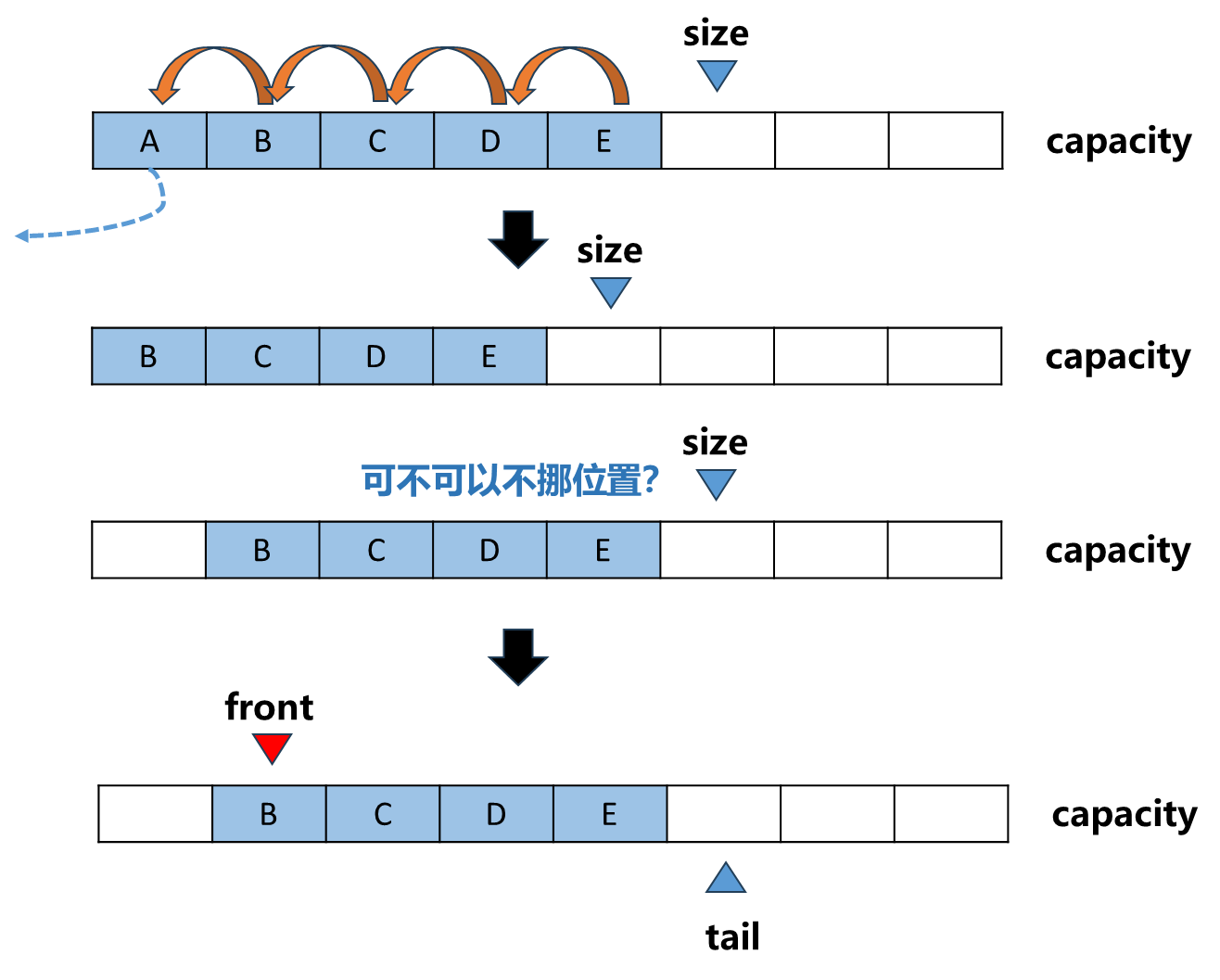
上面说到数组队列的实现存在一个局限性就是出队操作时间复杂度为O(n)O(n) ，如下图所示，假设此时数组队列可容纳的元素数是8个，此时队列有5个元素A、B、C、D、EA、B、C、D、E , 队首的元素A出队后，所有的元素都必须往前挪一个单位, 然后 size–.正是因为B、C、D、E都要往前移动一个位置，所以复杂度为O(n)O(n).

image-20251109205153093

一个很自然想法就是删完了元素A后，整个数组元素不挪位置, B C D E依然保持着队列的样子，B是队首，E是队尾.所以可以记录一下队首队尾是谁，如上图中最下面一行，用一个front指向队首，tail指向下一个新元素入队应该存储的位置即size。 因此当元素A移出数组后，我们要做的就是front++即可，而需要所有的元素向前挪动.

基于这样的想法就有了循环队列：

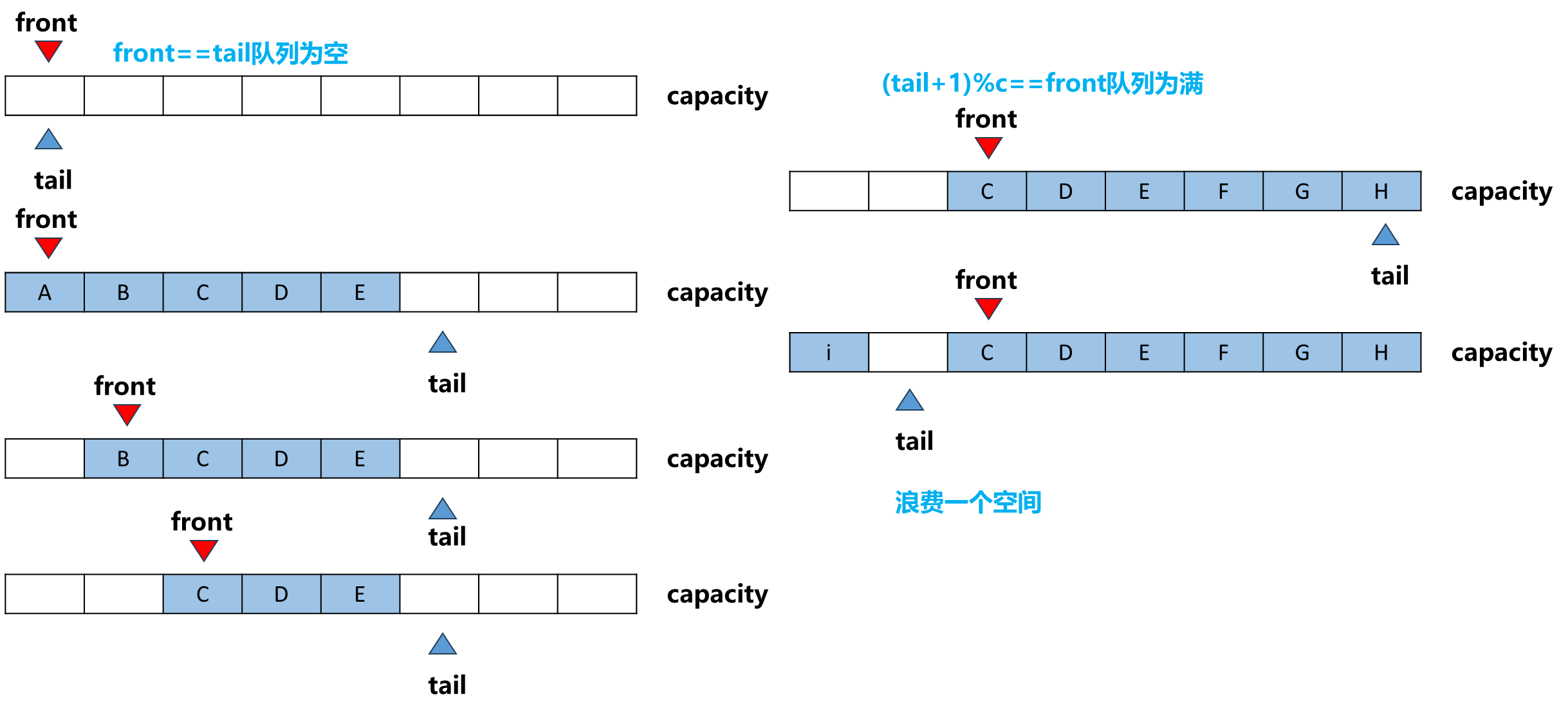
image-20251110012633554

  • 初始情况，队列中没有任何元素，front和tail都指向0，而front本来指向队列第一元素，而tail指向队列最后一个元素的后一个位置.但是当队列整体为空，front只好和tail指在一起.

  • 如果此时有元素入队了，则将tail++，假设队列加入了5个元素A、B、C、D、E. 此时如果要出队，只需front++, 如图中出队两次最终得到 C D E

  • 接着再有新元素F、G依次入队，tail++，再来一个新元素H,此时tail不能++，由于队首元素挪出数组以后前面的空间没有别后面的元素挤到，所以前面还有可以利用的空间，这就是循环队列的来由. 此时可以把数组看成一个环，一共可以容纳8个元素0-7，7之后的索引是0. 所有再有新元素i入队会放在索引0的位置，tail++。

  • 此时还有一个空的元素，还能放吗？要留意前面定义了front==tail为空的条件，此时如果再放入新元素tail++那么tail会等于front，但此时队列不为空，因此如果再放入新元素front==tail 的条件既可以表示队列为空和队列为满了，因此这个空间不能放入新元素.

  • 即(tail+1)%c==front时队列为满，对于循环队列来说，会浪费一个空间.

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
public class LoopQueue<E> implements Queue<E> {

    private E[] data;
    private int front, tail;
    private int size;

    public LoopQueue(int capacity) {
        data = (E[]) new Object[capacity+1];
        front = 0;
        tail = 0;
        size = 0;
    }

    public LoopQueue() {
        this(10);
    }

    public int getCapacity(){
        return data.length-1;
    }

    @Override
    public boolean isEmpty(){
        return front == tail;
    }

    @Override
    public int getSize(){
        return size;
    }

    @Override
    public void enqueue(E e){
        // 首先判断队列是否已满
        if((tail+1)%data.length == front)
            resize(getCapacity()*2);
        data[tail] = e;
        tail = (tail+1)%data.length;
        size++;
    }

    @Override
    public E dequeue(){
        if(isEmpty())
            throw new IllegalStateException("Queue is empty");

        E ret = data[front];
        data[front] = null;
        front = (front+1)%data.length;
        size--;
        if(size == data.length/4 && getCapacity()/2 !=0)
            resize(getCapacity()/2);
        return ret;
    }

    @Override
    public E getFront(){
        if(isEmpty())
            throw new IllegalStateException("Queue is empty");
        return data[front];
    }

    private void resize(int newCapacity){

        E[] newData = (E[]) new Object[newCapacity+1];
        for(int i=0; i<size; i++){
            newData[i] = data[(front+i) % data.length];
        }
        data = newData;
        front = 0;
        tail = size;
    }

    @Override
    public String toString(){

        StringBuilder res = new StringBuilder();
        res.append(String.format("Queue: size = %d, capacity = %d\n", size, getCapacity()));
        res.append("front [");
        for (int i = front; i != tail; i=(i+1)%data.length) {
            res.append(data[i]);
            if((i+1) % data.length != tail){
                res.append(", ");
            }
        }
        res.append("] tail");
        return res.toString();
    }

    public  static void main(String[] args){
        LoopQueue<Integer> queue = new LoopQueue<>();
        for  (int i = 0; i < 5; i++) {
            queue.enqueue(i);
            System.out.println(queue);

            if(i%3 ==2){
                queue.dequeue();
                System.out.println(queue);
            }

        }
    }

}

image-20251110161931669

通过上面的实现，数组队列出队操作时间复杂度O(n)O(n) ，对于循环队列变成了O(1)O(1).

复杂度分析

对于循环队列：

LoopQueue

  • void enqueue(E) 入队：向队列添加一个元素 O(1)
  • E dequeue() 出队：从队列取出一个元素 **O(1) **
  • E getFront() 查看队首元素 O(1)
  • int getSize() 队列元素数量 O(1)
  • boolean isEmpty() 判断队列是否为空 O(1)

测试数组队列和循环队列 出队和入队耗时：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
import java.util.Random;

public class Main {

    // 测试使用q运行opCount个enqueueu和dequeue操作所需要的时间，单位：秒
    private static double testQueue(Queue<Integer> q, int opCount){

        long startTime = System.nanoTime();

        Random random = new Random();
        for(int i = 0 ; i < opCount ; i ++)
            q.enqueue(random.nextInt(Integer.MAX_VALUE));
        for(int i = 0 ; i < opCount ; i ++)
            q.dequeue();

        long endTime = System.nanoTime();

        return (endTime - startTime) / 1000000000.0;
    }

    public static void main(String[] args) {

        int opCount = 100000;

        ArrayQueue<Integer> arrayQueue = new ArrayQueue<>();
        double time1 = testQueue(arrayQueue, opCount);
        System.out.println("ArrayQueue, time: " + time1 + " s");

        LoopQueue<Integer> loopQueue = new LoopQueue<>();
        double time2 = testQueue(loopQueue, opCount);
        System.out.println("LoopQueue, time: " + time2 + " s");
    }
}

image-20251110162917849

上面结果显示可以发现，对于10W次出队和入队操作，ArrayQueue耗时12.67s，而LoopQueue只需0.004s左右. 这个差距主要就是出队操作上的不同.