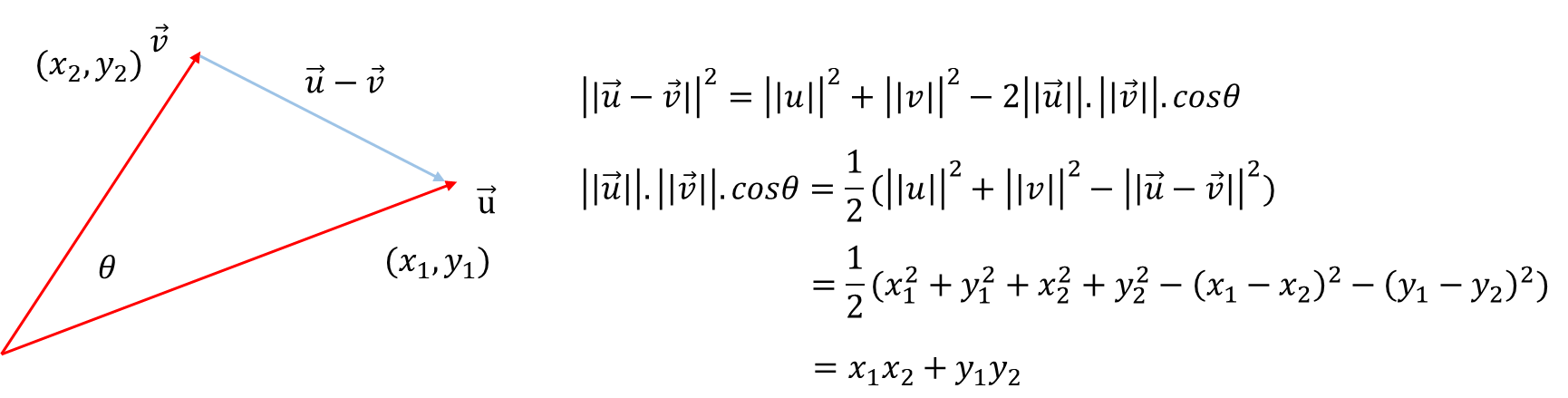Linear Algebra(1):向量2025.11.141 Categories / 1 Tags
Blog Post

Linear Algebra(1):向量

2025.11.14线性代数线性代数
Linear Algebra(1):向量

线性代数

Introduction

线性代数是我们高等教育理工科学生必学的数学，毫不夸张的说线性代数是近现代科学发展过程中最重要的基础数学之一.为什么线性代数这么重要？

我们在初等教育中即小学中学这个阶段，代数更多的是在研究一个一个的数，比如对数进行具体的分类为$N\quad Q\quad R$ 即自然数、有理数、实数，进而在代数领域一个非常重要的研究课题是函数$f(x)$， 函数可以理解为将一个数传入一个规则中得到另外一个结果.这些代数中主要研究的对象是一个一个的数.

高等教育阶段的线性代数对这个概念进行了拓展，简单来说线性代数在研究”一组数”，即向量. 线性代数研究的是所谓的空间$N^n$, $Q^n$, $R^n$ ,同样线性代数领域也要研究很多的函数$T(\vec{v})$ ，这个函数作用的对象通常是一个向量，线性代数中的矩阵就可以理解为对向量进行变化的函数.

初等代数我们研究的是一个一个的数，高等教育线性代数研究的是一个一个的向量(一组数):
$$
x\quad\rightarrow \quad \vec{x}=(x_1\quad x_2 \quad … \quad x_n)
$$
为什么要研究一组数呢？背后原因也很简单，真实世界是多维度的，单变量不足描述真实世界，用单变量描述真实世界是不方便的。而线性代数将研究对象拓展到向量维度，可以对多维数据进行统一的研究进而演化出一套计算的方法和工具，可以更加方便非常契合应用到真实世界中。因此近乎所有的理工科教材都充斥着线性代数的公式或符号。

向量

什么是向量

线性代数的学习从向量开始。上面提到了线性代数据之所非常重要，是其从研究一个数拓展到研究一组数。这样对于表达我们的多维世界来说非常方便。那么究竟怎样表达一组数呢？

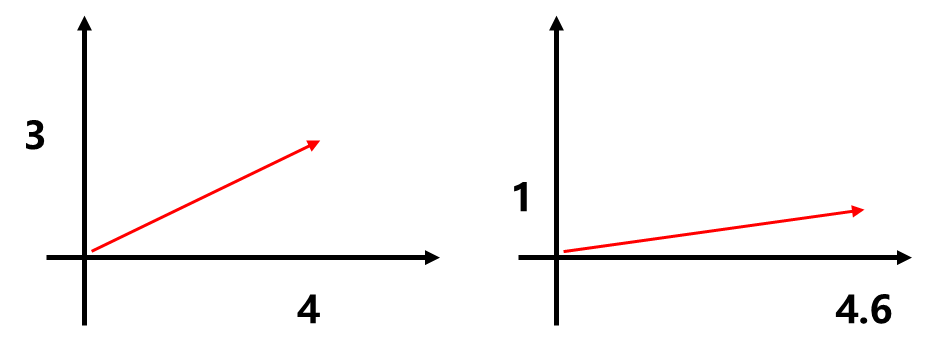
一组数的基本表示方法就是向量（vector）,向量也是线性代数研究的基本元素。一组数有什么用？向量概念的产生最基本的出发点就是为了表示方向，一组数可以更好的表示方向这个概念，也是“向”的来源。比如下面的二维平面中，我们从一点出发到另外一点，假设从起点到终止点的距离是5km,从同样一个起始点出发，很可能会达到一个不同的终止点，只使用5这个数字表示最终走到哪里是远远不够的。此时向量就有了意义，比如（4，3）和（4.6，1）两个数字才能准确表达位置的不同。

image-20251113123421701

这是一个物理学中位移概念的例子，同样像速度、加速度、力等概念都具有方向的概念。那么我们研究过程中只考虑方向吗？起始点重要吗？从（0，0）到（4，3）和从（-1，-1）到（3，2）其实是一样的，它们的区别只在于坐标系不同。向量只表征从一个点到另一个点响应的结果而不区分这一过程是从哪个起始点出发的，所以为了研究方便这个起始点统一都理解成从原点开始。

但是向量的顺序是重要的！（4，3）和（3，4）是截然不同的，即向量也是一组有序的数。如果只是表示物理世界的方向，最多三个维度就够了，因为我们的世界在人类感知中是一个三维的空间. 但是为了扩大研究范围同时也增强向量这个数学概念的能力，可以用抽像的n维向量描述n维世界. 我们无法直接感知4维空间和5空间它是什么样子的，看不见也画不出来，只能抽象的理解它。

举一个用高维空间表达事物的例子，比如刻画一个房子：

面积 卧室 卫生间 最近地铁站 价格（万）
108 3 2 1 320

每一个数字都是一个维度，不同的房子每一个数字可能不同，所以每一个房子都可以使用（108，3，2，1，320）这样的5个数字来表示，即5维向量，此时向量就是一组数，这组数的含义由使用者定义。

向量都是一组有序的数字，可以用两个视角来看待它。一个视角可以将其看作一个方向，另外一个视角看作一个有序的数字，可以理解为高维空间的一个数据点。这两个视角可以互相转换，一个方向就是一个点，空间中的任何一点都可以看做从原点指向这个点的一个方向。实际使用线性代数过程中，更倾向于第二个视角把每个向量看做空间中的一个点，但在学习向量性质时使用方向的视角会更加形象直观。这两个视角一个是一个有向线段，一个是空间的点。

向量的术语和表示法

和向量相对应的一个数字，称为标量。我们学的代数，用符号代表数。和标量相区别的是，向量的符号画箭头：$\vec{v}$.个别情况下，尤其是几何学中，像我们高中做的向量几何题目，我们会考虑向量的起始点，比如$\vec{OA}$ ，假如O(0,0),A(4，3)，B(-1,-1),C(3，2）,此时的$\vec{OA}$ 和$\vec{BC}$ 是不一样的，因为几何学这两个线段不同。但是从线性代数角度出发这两个向量是同样的向量，不考虑起点。

向量也分为行向量和列向量。比如（3，4）一组数写成一行就是行向量，而$(3，4)^T$ 写成一列就是列向量。现阶段行向量和列向量没有区别，并且通常教材论文提到向量通常指列向量。

代码实现：

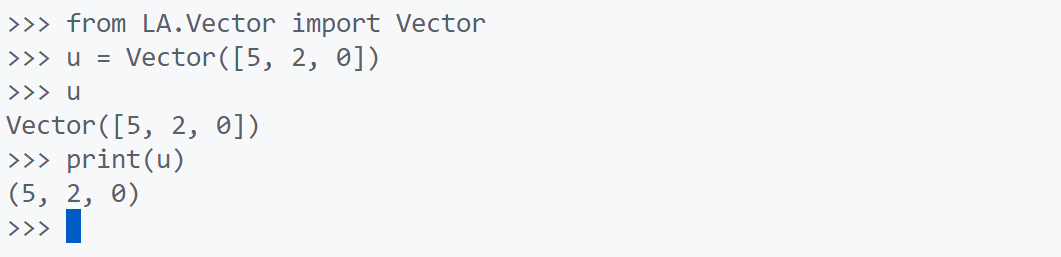
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Vector:

    def __init__(self, lst):
        self._values = lst
    
    def __len__(self):
        '''返回向量长度'''
        return len(self._values)

    def __getitem__(self, idx):
         '''返回指定索引元素'''
        return self._values[idx]

    def __repr__(self):
        return "Vector({})".format(self._values)
    
    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))

image-20251113132203748

如上图所示，其中__repr__方法是系统调用的，而__str__ 是用户调用的. __repr__方法表示的是类的对象对应的构造方法应该写成什么样子，而__str__方法就是从用户角度来看这个对象是什么样子的。

向量的两个基本运算

向量的基本运算主要包括两种运算：

  • 向量加法 (两个向量之间)

$$
(5,2)^T+(2,5)^T=(7，7)^T\
(a,b)^T+(c,d)^T=(a+b，c+d)^T\
\begin {pmatrix}a \b \c\end {pmatrix} +
\begin {pmatrix}d \e \f\end {pmatrix}=
\begin {pmatrix}a+d \b+e \c+f\end {pmatrix}\
\begin {pmatrix}v_1 \v_2 \…\v_n\end {pmatrix} +
\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}=
\begin {pmatrix}v_1+u_1 \v_2+u_2 \…\u_n+v_n\end {pmatrix}\
$$

  • 数量乘法(一个标量和一个向量)

$$
2\times(5,2)^T=(10, 4)^T\
k\times(a,b)^T=(ka, kb)^T\
k\begin {pmatrix}v_1 \v_2\… \v_n\end {pmatrix} =
\begin {pmatrix}k.v_1 \k.v_2\… \k.v_n\end {pmatrix}\
$$

代码实现：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class Vector:

    def __init__(self, lst):
        self._values = list(lst) # immutable
    
    def __add__(self, another):
        assert len(self) == len(another), \
        "length of vectors must be same"

        return Vector([a + b for a, b in zip(self, another)])
    
    def __sub__(self, another):
        assert len(self) == len(another), \
        "length of vectors must be same"

        return Vector([a - b for a, b in zip(self, another)])

    def __mul__(self, k):
        '''返回数量乘法结果 self*k'''
        return Vector([k*e for e in self])      
    
    def __rmul__(self, k):
        '''返回数量乘法结果 k*self'''
        return self*k

    def __pos__(self):
        '''返回向量取正的结果向量'''
        return 1*self

    def __neg__(self):
        '''返回向量取负的结果向量'''
        return -1*self    

    def __iter__(self):
        '''返回向量迭代器''' # pythonic
        return self._values.__iter__()
    
    def __len__(self):
        '''返回向量长度'''
        return len(self._values)

    def __getitem__(self, idx):
        return self._values[idx]

    def __repr__(self):
        return "Vector({})".format(self._values)
    
    def __str__(self):
        return "({})".format(", ".join(str(e) for e in self._values))
  • 测试代码
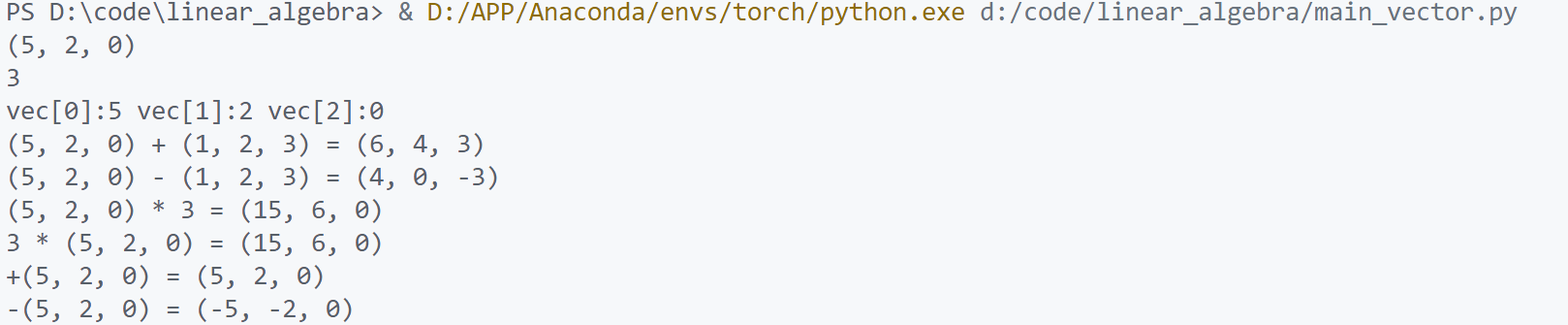
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
from LA.Vector import Vector

if __name__ == "__main__":

    vec = Vector([5, 2, 0])
    print(vec)
    print(len(vec))
    print("vec[0]:{} vec[1]:{} vec[2]:{}".format(vec[0], vec[1], vec[2]))

    vec2 = Vector([1, 2, 3])
    print("{} + {} = {}".format(vec, vec2, vec+vec2))
    print("{} - {} = {}".format(vec, vec2, vec-vec2))

    print("{} * {} = {}".format(vec, 3, vec*3))
    print("{} * {} = {}".format(3, vec, 3*vec))

    print("+{} = {}".format( vec, +vec))
    print("-{} = {}".format( vec, -vec))

image-20251113150313115

向量运算的基本性质

  • 交换律：$\vec{u}+\vec{v}=\vec{v}+\vec{u}$
  • 结合律：$(\vec{u}+\vec{v})+\vec{w}=\vec{u}+(\vec{v}+\vec{w})$
  • 数乘分配律：$k(\vec{u}+\vec{v})=k\vec{u}+k\vec{v}$ ，$(k+c)\vec{u}=k\vec{u}+c\vec{u}$ ，$(kc)\vec{u}=k(c\vec{u})$ ，$1\vec{u}=\vec{u}$

证明举例:
$$
Prof.\quad \quad k(\vec{u}+\vec{v})=k\vec{u}+k\vec{v}\
k(\vec{u}+\vec{v})=k(\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}+\begin {pmatrix}v_1 \v_2\… \v_n\end {pmatrix})=k\begin {pmatrix}u_1+v_1 \u_2+v_2\… \u_n+v_n\end {pmatrix}=\begin {pmatrix}ku_1+kv_1 \ku_2+kv_2\… \ku_n+kv_n\end {pmatrix}\
k\vec{u}+k\vec{v}=k\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}+k\begin {pmatrix}v_1 \v_2\… \v_n\end {pmatrix}=\begin {pmatrix}ku_1 \ku_2 \…\ku_n\end {pmatrix}+\begin {pmatrix}kv_1 \kv_2\… \kv_n\end {pmatrix}=\begin {pmatrix}ku_1+kv_1 \ku_2+kv_2\… \ku_n+kv_n\end {pmatrix}
$$

零向量

向量的世界里既然定义好了加法，那么相应的和数的世界一样，我们一样可以定义一个零。所谓的零向量也是各个维度都是零的向量，我们不定义什么是零向量，我们从推导一个性质出发，而这个性质和数字世界中0的这个数字的性质非常像.

对于任意一个向量$\vec{u}$ ,都存在一个向量$O$ ，满足$\vec{u}+O=\vec{u}$ .

假设存在这样一个向量$\vec{O}$ ,证明其存在性
$$
\vec{u}=\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}\quad\vec{O}=\begin {pmatrix}o_1 \o_2 \…\o_n\end {pmatrix}\
\vec{u}+O=\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}+\begin {pmatrix}o_1 \o_2 \…\o_n\end {pmatrix}=\begin {pmatrix}u_1+o_1 \u_2+o_2 \…\u_n+0_n\end {pmatrix}=\begin {pmatrix}u_1 \u_2 \…\u_n\end {pmatrix}\
\begin {cases}
u_1+o_1=u_1 \
u_2+o_2=u_2 \
…\
u_n+o_n=u_n \
\end{cases} \quad
\begin {cases}
o_1=0 \
o_2=0 \
…\
o_n=0 \
\end{cases} \rightarrow O=\begin {pmatrix}
0 \
0 \
…\
0 \
\end{pmatrix}
$$
我们称这个向量为零向量.注意：这个$O$ 是没有箭头的.有了零向量，我们相应可以定义负这个概念。

对于任意一个向量$\vec{u}$ ,都存在一个向量$-\vec{u}$ ，满足$\vec{u}+-\vec{u}=O$ .

零向量实现：在上面的Vector类中假如下面类方法

1
2
3
@classmethod
def zero(cls, dim):
    return cls([0]*dim)

向量的长度和单位向量

看待向量有两种方式，其中一种是把向量看成一个有向的线段，它是从原点一直指向空间中的某一个点这样一个方向。既然是有向线段那么除了方向也有大小.比如二维向量$\vec{u}=(3,4)$ 的大小可以根据勾股定理求出为5. 在线性代数数学表示上，我们会使用$||\vec{u}||$ 用它来表示向量的长度大小，即向量的模。

对于n维向量$\vec{u}=(u_1,u_2,…,u_n)^T$ ，那么$\vec{u}$ 的模：
$$
||\vec{u}||=\sqrt{u_1^2+u_2^2+…+u_n^2}
$$
知道如何求向量的长度后，就可以引入一个新的概念单位向量(unit vector).所谓单位向量即其长度固定为1个单位，每一个向量都对应着一个单位向量$\hat{u}$。
$$
\hat{u}=\frac{1}{||\vec{u}||}.\vec{u}=(\frac{u_1}{||\vec{u}||}, \frac{u_2}{||\vec{u}||},…,\frac{u_n}{||\vec{u}||})\
||\hat{u}||=1\quad 只表示方向
$$
根据$\vec{u}$ 求出$\hat{u}$ 的过程有时称为归一化，规范化(normalize).

单位向量有无数个，比如二维平面的以原点为圆心半径为1的圆上的向量都是一个单位向量。不过二维空间有两个很特殊的单位向量即和二维平面两个轴重合的单位向量$\vec{e_1}=(1,0), \vec{e_2}=(0,1).$ 为什么表示为小e呢？因为这两个单位向量只由0，1组成，叫做标准单位向量(Standard Unit Vector).标准单位向量指向坐标轴正方向.

三维空间就有三个标准单位向量$\vec{e_1}=(1,0,0), \vec{e_2}=(0,1,0).\vec{e_3}=(0,0,1).$

n维空间就有n个标准单位向量$\vec{e_1}=(1,0,…,0), \vec{e_2}=(0,1,…,0).\vec{e_3}=(0,0,…,1).$

标准单位向量是很重要的一组向量，整个空间坐标系是由标准单位向量所组建的。

代码实现求向量的模：（放到Vector类中）

1
2
3
4
5
6
7
8
9
10
11
12
13
def norm(self):
    '''求向量的模'''
    return math.sqrt(sum(e**2 for e in self._values))

def normalize(self):
    '''求改向量的单位向量'''
    if self.norm() < EPSILON:
        raise ZeroDivisionError("norm is zero")
    return Vector(self._values)/self.norm()

def __truediv__(self, k):
    '''返回数量除法'''
    return (1/k)*self

这里实现__truediv__ 方法来使得我们的Vector能够除以一个数，考虑到零向量求方向向量会抛出除0异常，同时normalize方法捕捉异常.

向量的点乘

前面定义了向量的两个基本运算，其中加法是两个向量的运算，数量乘法是一个向量和一个标量的运算. 但是对于两个向量相乘这样的运算并没有定义.

两个向量相乘可能比较自然的想法就是：
$$
\vec{u}.\vec{v}=\begin {pmatrix}u_1\ u_2\…\u_n \end {pmatrix}.\begin {pmatrix}v_1\ v_2\…\v_n \end {pmatrix}=\begin {pmatrix}u_1.v_1\ u_2.v_2\…\u_n.v_n \end {pmatrix}
$$
跟加法一样对应元素相乘组合成一个向量，实际上对于两个向量相乘的运算并不是这样定义的!（上面是错的）为什么不这么定义？后续分晓…

线性代数中真正两个向量相乘的定义是这样的：
$$
\vec{u}.\vec{v}=\begin{pmatrix}u_1 \ u_2\…\u_n\end{pmatrix}.\begin{pmatrix}v_1 \ v_2\…\v_n\end{pmatrix}=sum(\begin{pmatrix}u_1.v_1 \ u_2.v_2\…\u_n.v_n\end{pmatrix})=u_1.v_1+u_2.v_2+…+u_n.v_n\=||\vec{u}||.||\vec{v}||.cos\theta
$$
可以看出来两个向量“相乘”后的结果是一个数(标量)，而不是一个向量.这种向量的乘法叫做向量的点乘或者内积.为什么这么定义？后续揭晓.同时这样定义点乘后，上面的结果在几何上同时还等于$||\vec{u}||.||\vec{v}||.cos\theta$ .

证明一下这个结论：
$$
\vec{u}.\vec{v}=u_1.v_1+u_2.v_2+…+u_n.v_n=||\vec{u}||.||\vec{v}||.cos\theta
$$
二维空间中：
$$
\vec{u}.\vec{v}=x_1.x_2+y_1.y_2=||\vec{u}||.||\vec{v}||.cos\theta
$$
image-20251114140028454

如上图所示,采用余弦定理得证. 同理可以拓展到n维空间，得证上式.

代码实现向量点乘操作：

1
2
3
4
5
6
def dot(self, another):
    '''向量点乘, 返回标量结果'''    
    assert len(self) == len(another), \
    "Error in dot product.Length of vectors must be same"

    return sum(a*b  for a, b in zip(self, another))

有些数学库会将$uv$ 定义为逐元素相乘的向量，即：
$$
\vec{u}\vec{v}=\begin {pmatrix}u_1\ u_2\…\u_n \end {pmatrix}.\begin {pmatrix}v_1\ v_2\…\v_n \end {pmatrix}=\begin {pmatrix}u_1.v_1\ u_2.v_2\…\u_n.v_n \end {pmatrix}
$$
称为element-wise multiplication.由于这个计算不具备数学含义，在我们的现实中不取.

向量点乘的应用意义

向量点乘定义：
$$
\vec{u}.\vec{v}=u_1.v_1+u_2.v_2+…+u_n.v_n=||\vec{u}||.||\vec{v}||.cos\theta
$$
从数学计算上其等于每一个向量的分量相乘再相加，几何意义上等于两个向量的模再乘以两个向量的夹角cos.

这个式子最简单的一个应用就是非常容易的求出两个向量的夹角：
$$
cos\theta=\frac{\vec{u}.\vec{v}}{||\vec{u}||.||\vec{v}||}
$$
特别的如果$\theta=90^{\circ},\vec{u}.\vec{v}=0$. 反之如果$\vec{u}.\vec{v}=0$ ,两个向量垂直. 如果$\vec{u}.\vec{v}>0$ ,两个向量夹角为锐角;如果$\vec{u}.\vec{v}<0$ ,两个向量夹角为钝角.

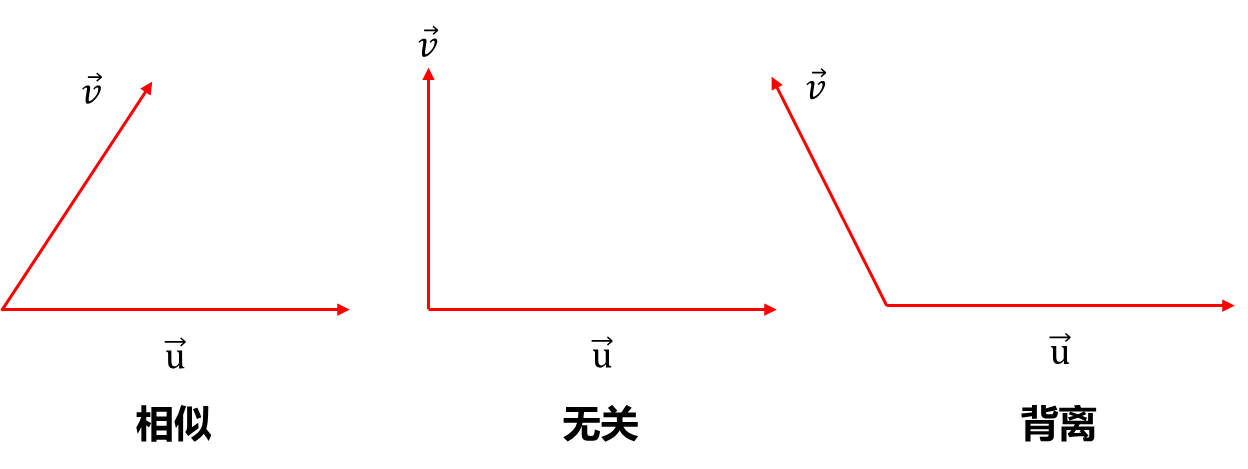
因此首先一个应用就是判断两个向量的相似程度(推荐系统)：

image-20251114144916943

另一个应用就是几何计算:

image-20251114145952114

Numpy中向量的基本使用

最后附上业界经常使用的线性代数库Numpy的基本使用方法，很多框架比如机器学习框架scikit-learn中的数据都是要以numpy所定义的矩阵类相应的对象传进机器学习算法中.

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
import numpy as np

if __name__ == "__main__":

    print(np.__version__)

    # np.array 基础
    lst = [1, 2, 3]
    lst[0] = "Linear Algebra"
    print(lst)

    vec = np.array([1, 2, 3])
    print(vec)
    # vec[0] = "Linear Algebra"
    # vec[0] = 666
    # print(vec)

    # np.array的创建
    print(np.zeros(5))
    print(np.ones(5))
    print(np.full(5, 666))

    # np.array的基本属性
    print(vec)
    print("size =", vec.size)
    print("size =", len(vec))
    print(vec[0])
    print(vec[-1])
    print(vec[0: 2])
    print(type(vec[0: 2]))

    # np.array的基本运算
    vec2 = np.array([4, 5, 6])
    print("{} + {} = {}".format(vec, vec2, vec + vec2))
    print("{} - {} = {}".format(vec, vec2, vec - vec2))
    print("{} * {} = {}".format(2, vec, 2 * vec))
    print("{} * {} = {}".format(vec, vec2, vec * vec2))
    print("{}.dot({}) = {}".format(vec, vec2, vec.dot(vec2)))

    print(np.linalg.norm(vec))
    print(vec / np.linalg.norm(vec))
    print(np.linalg.norm(vec / np.linalg.norm(vec)))

    # zero3 = np.zeros(3)
    # print(zero3 / np.linalg.norm(zero3))