线性代数

Matrix Application

矩阵在图形变换中的应用

对于一个二维平面，如果让每个点的横坐标扩大a倍，纵坐标扩大b倍，那么就可以设计下面的变换矩阵T:
$$
T=\begin{pmatrix}
a & 0\
0 & b
\end{pmatrix}
\quad
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
a & 0\
0 & b
\end{pmatrix}.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
ax\
by
\end{pmatrix}
$$
让每个点关于x轴翻转：
$$
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
x\
-y
\end{pmatrix}\
T=\begin{pmatrix}
1 & 0\
0 & -1
\end{pmatrix}
$$
让每个点关于y轴翻转：
$$
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
-x\
y
\end{pmatrix}\
T=\begin{pmatrix}
-1 & 0\
0 & 1
\end{pmatrix}
$$
让每个点关于原点翻转(x轴，y轴均翻转)：
$$
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
-x\
-y
\end{pmatrix}\
T=\begin{pmatrix}
-1 & 0\
0 & -1
\end{pmatrix}
$$
同时这里关于原点翻转可以看做x轴，y轴均翻转：
$$
T_x=\begin{pmatrix}
1 & 0\
0 & -1
\end{pmatrix} \quad
T_y=\begin{pmatrix}
-1 & 0\
0 & 1
\end{pmatrix} \
T_y.(T_x.\begin{pmatrix}
x\
y
\end{pmatrix})=(T_y.T_x).\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
-1 & 0\
0 & -1
\end{pmatrix}\begin{pmatrix}
x\
y
\end{pmatrix}
$$
沿x轴方向错切：
$$
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
x+ay\
y
\end{pmatrix}\
T=\begin{pmatrix}
1&a\
0&1
\end{pmatrix}
$$
沿y轴方向错切：
$$
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
x\
bx+y
\end{pmatrix}\
T=\begin{pmatrix}
1&0\
b&1
\end{pmatrix}
$$
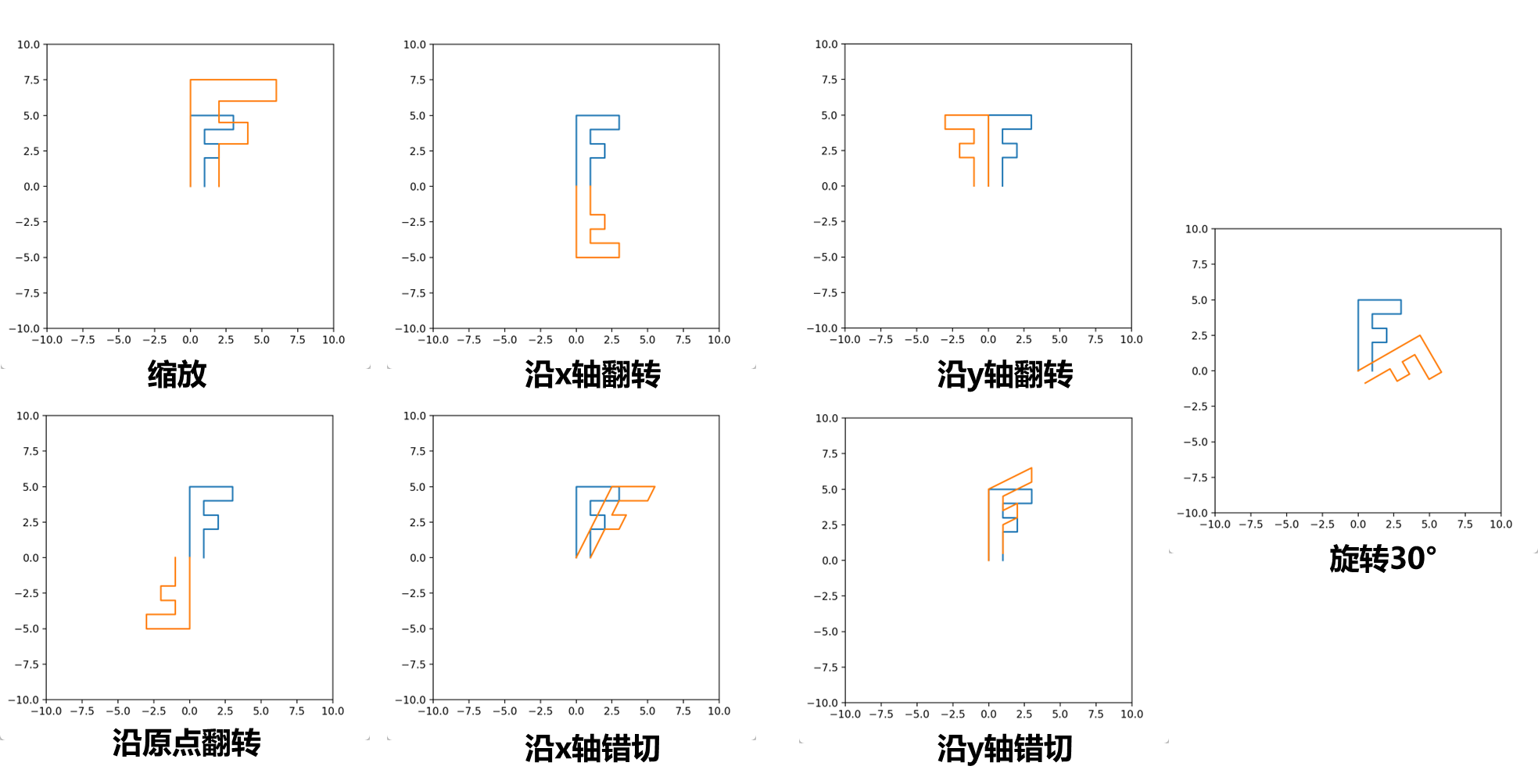
上面这些变换矩阵可以在二维平面上对一个点进行各种不同的变换，包括缩放、翻转、错切.

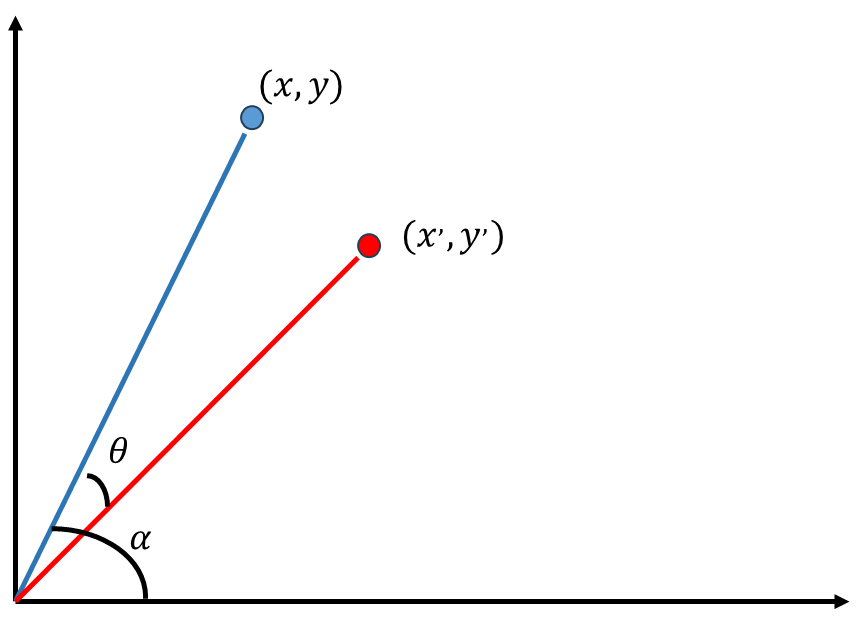
接下来介绍下一个非常常见的变换，矩阵的旋转变换. 旋转操作依然需要找到一个矩阵$T$ 将$(x,y)^T$ 转换为另外一个坐标.如果如下图所示将一个点$(x,y)^T$ 关于原点顺时针旋转$\theta$ 角，最终得到的这个坐标$(x^,,y^,)$是多少？

假设$(x,y)^T$ 的模是d, 那么有：
$$
cos\alpha.d=x \quad d=\frac{x}{cos\alpha} \quad d=\frac{x^,}{cos(\alpha-\theta)}\
sin\alpha.d=y \quad d=\frac{y}{sin\alpha} \quad d=\frac{y^,}{cos(\alpha-\theta)}
$$
进一步可得：
$$
x^,=\frac{cos(\alpha-\theta)}{cos\alpha}x \quad y^,=\frac{sin(\alpha-\theta)}{sin\alpha}y
$$
使用余弦差角公式可得：
$$
x^,=\frac{cos\alpha cos\theta+sin\alpha sin\theta}{cos\alpha}x\
= cos\theta.x+sin\theta \frac{sin\alpha}{cos\alpha}x\
=cos\theta.x+sin\theta \frac{y}{x}x\
=cos\theta.x+sin\theta y
$$
同理可得：
$$
y^,=cos\theta .y-sin\theta .x
$$
因此有：
$$
T.\begin{pmatrix} x\y\end{pmatrix}=\begin{pmatrix} cos\theta.x+sin\theta. y\-sin\theta .x+cos\theta .y\end{pmatrix}\
T=\begin{pmatrix} cos\theta &sin\theta\-sin\theta & cos\theta\end{pmatrix}
$$
这样的变换矩阵T就是图形学中能够使任意一个点沿原点旋转$\theta$ 角.

上面的思路同样可以拓展到三维坐标中，同时注意上面并不包含平移操作即将点坐标沿x轴或y轴平移一定的单位，主要是因为上面的思路是求不出T可以完成这种平移操作，但图形学中有一个非常成熟的解决这个问题的方案叫做仿射变换.

代码示例：

import matplotlib.pyplot as plt
from LA.Matrix import Matrix
from LA.Vector import Vector
import math

if __name__ == "__main__":
    points = [[0,0], [0,5], [3,5], [3,4], [1,4],
              [1,3], [2,3], [2,2], [1,2], [1,0]]
    
    x = [point[0] for point in points]
    y = [point[1] for point in points]

    plt.figure(figsize=(5,5))
    plt.xlim(-10,10)
    plt.ylim(-10,10)
    plt.plot(x,y)
    # plt.show()

    P = Matrix(points)

    T =Matrix([[2, 0], [0, 1.5]])
    T =Matrix([[1, 0], [0, -1]])
    T =Matrix([[-1, 0], [0, 1]])
    T =Matrix([[-1, 0], [0, -1]])
    T =Matrix([[1, 0.5], [0, 1]])
    T =Matrix([[1, 0], [0.5, 1]])

    theta = math.pi/3
    T= Matrix([[math.cos(theta), math.sin(theta)], [-math.sin(theta), math.cos(theta)]])

    P2 = T.dot(P.T())
    plt.plot([P2.col_vector(i)[0] for i in range(P2.col_num())],
             [P2.col_vector(i)[1] for i in range(P2.col_num())])
    plt.show()

如上图所示，这些图形变换效果的变换矩阵T都已提及，可以发现沿y轴错切的效果有点像书本翻开的效果，实际上不断调正矩阵变换错切的参数后在计算机屏幕上连续绘制，最终就可以通过变换矩阵形成一个书本翻页的效果. 从网页中基础的动画、移动端app上的动画以及很多影视特效都离不开这些最基础最简单的图形学操作，这些都是基于线性代数的.

单位矩阵

如果让每个点的横坐标扩大a倍，纵坐标扩大b倍，那么变换矩阵T如下形式:
$$
T=\begin{pmatrix}
a & 0\
0 & b
\end{pmatrix}
\quad
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
a & 0\
0 & b
\end{pmatrix}.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
ax\
by
\end{pmatrix}
$$
如果让每个点的横坐标扩大1倍，纵坐标扩大1倍，此时T:
$$
T=\begin{pmatrix}
1 & 0\
0 & 1
\end{pmatrix}
\quad
T.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
1 & 0\
0 & 1
\end{pmatrix}.\begin{pmatrix}
x\
y
\end{pmatrix}=\begin{pmatrix}
x\
y
\end{pmatrix}
$$
任意一个$(x,y)^T$ 和T相乘得到的结果都是其自身，即变换矩阵没有对点坐标产生任何变换，这样的矩阵就称为单位矩阵.

通常将单位矩阵记作$I$ :
$$
I_2=\begin{pmatrix}
1 & 0\
0 & 1
\end{pmatrix} \quad
I_3=\begin{pmatrix}
1 & 0 & 0\
0 & 1 & 0 \
0 & 0 & 1
\end{pmatrix} \quad
I_n=\begin{pmatrix}
1 & 0 &…& 0\
0 & 1 & …&0 \
…&…&…&…\
0 & 0 & …&1
\end{pmatrix} \quad \
I_n=(i_{kj})\begin{cases}
1 &if&k=j\
0 &if&k\ne j\

\end{cases}\
I.A=A \quad A.I=A
$$
显然单位矩阵一定是方阵. 单位矩阵在矩阵运算中的作用相当于数字中的1的作用.

矩阵的逆

有了单位矩阵就可以相应引入矩阵的逆的概念了。回忆一下数字系统中$x.(x^{-1})=1,(x\ne0)$ ,同理在矩阵中$AB=BA=I$ , 则称B是A的逆矩阵，记做$B=A^{-1}$ 。

数字系统中只有数字0不存在逆，但是矩阵世界中能找到无数个矩阵是不存在逆的.所以对于一个矩阵A来说，如果能找到其逆矩阵B的话，则称A为可逆矩阵，或者叫做非奇异矩阵(non-singular).

有些矩阵是不可逆的！称为不可逆矩阵，或者奇异矩阵(singular).

如果$BA=I$ ，则称B是A的左逆矩阵.
如果$AC=I$ , 则称C是A的右逆矩阵.

如果一个矩阵A既存在左逆矩阵B,又存在右逆矩阵C，则B=C.
$$
Prof.\quad BA=I \quad AC=I\
B(AC)=BI\
(BA)C=BI\
IC=BI\
C=B
$$
对于矩阵A，存在矩阵B，满足$AB=BA=I$ ,矩阵A可逆. 可以发现如果一个矩阵逆既能和A左乘又能右乘，因此A一定是个方阵.

可逆矩阵一定为方阵
非方阵一定不可逆

看到这里其实也可以回答出上篇矩阵幂的一个问题：
$$
A^0=I \quad A^{-1} \quad A^{-2}=(A^{-1})^2
$$
代码实现：(放入Matix类中)

@classmethod
def identity(cls, n):
    '''返回一个n行n列的单位矩阵'''
    m = [[0]*n for _ in range(n)]
    for i in range(n):
        m[i][i] = 1;
    return cls(m)

矩阵逆的性质

1.对于矩阵A，如果存在逆矩阵B，则B唯一.

反证法：假设矩阵A存在两个不同的逆矩阵B和C
$$
AB=AC=I\
B(AB)=B(AC)\
(BA)B=(BA)C\
B=C
$$
2.$(A^{-1})^{-1}=A$
$$
Prof. \quad A^{-1}.A=I \quad A.A^{-1}=I \
(A^{-1})^{-1}=A
$$
3.$(A.B)^{-1}=B^{-1}A^{-1}$
$$
Prof. \quad (AB).(B^{-1}A^{-1})=I \quad (B^{-1}A^{-1}).(AB)=I \
(AB).(B^{-1}A^{-1})=A(B^.B^{-1})A^{-1}=A.I.A^{-1}=I \
(B^{-1}A^{-1}).(AB)=B^{-1}(A^{-1}A)B=B^{-1}IB=I
$$
4.$(A^T)^{-1}=(A^{-1})^T$
$$
Prof. \quad A^T.(A^{-1})^T=I \quad (A^{-1})^T.A^T=I\
A^T.(A^{-1})^T=(A^{-1}.A)^T=I\
(A^{-1})^T.A^T=(A.A^{-1})^T=I
$$

用矩阵表示空间

回忆矩阵和向量相乘：
$$
\begin{cases}
x+2y=3 \
4x+5y=6
\end{cases}
\quad
\begin{pmatrix}
1&2 \
4&5
\end{pmatrix}
\begin{pmatrix}
x \
y
\end{pmatrix}

\begin{pmatrix}
3 \
6
\end{pmatrix}
$$

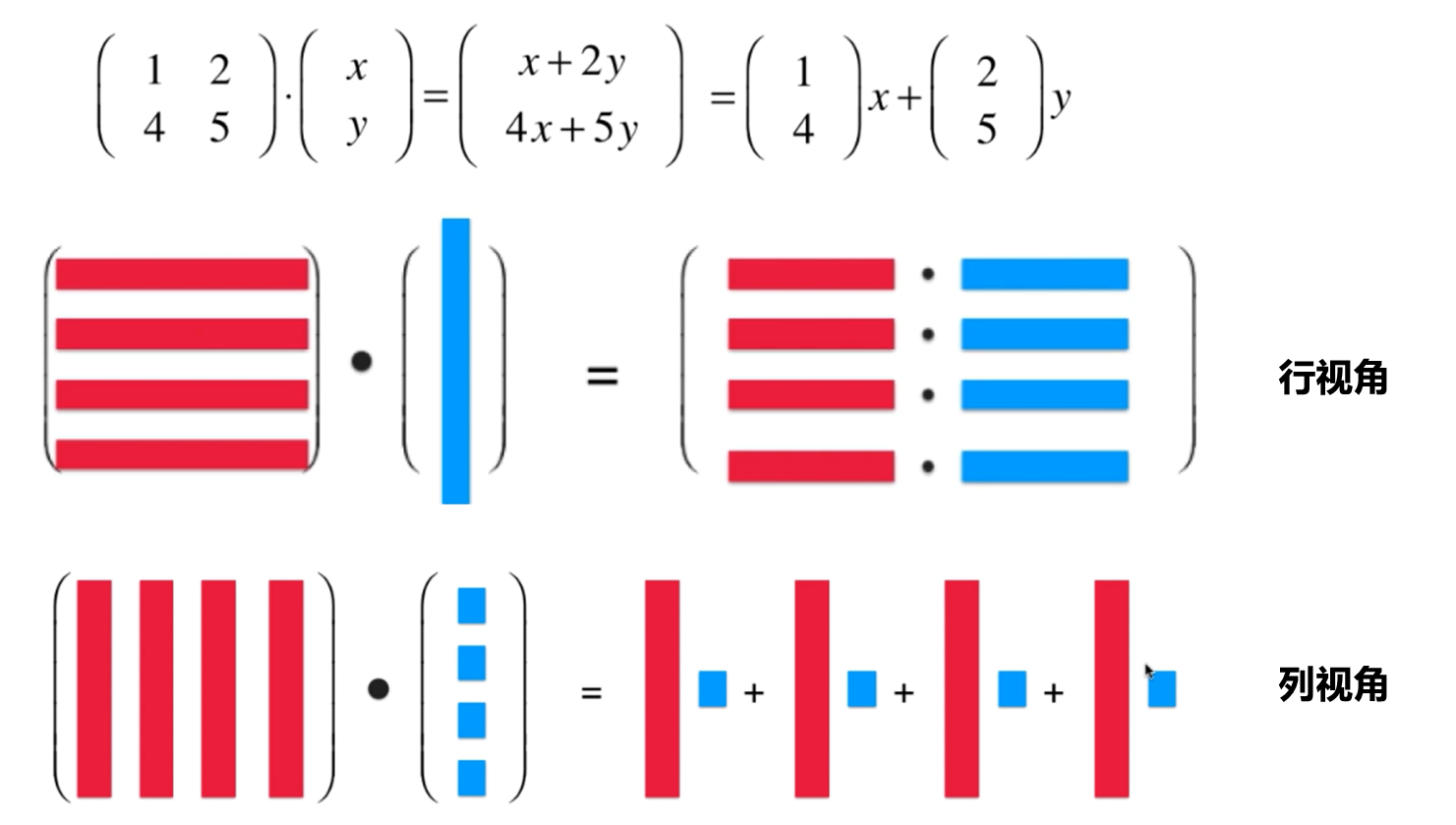
对于上面的方程组，可以使用矩阵的形式表示出来，既可以使用行视角来看待也可以使用列视角来看.

其中使用列视角来看待矩阵和向量相乘是非常有意义的：
$$
\begin{pmatrix}
1&0 \
0&1\end{pmatrix}.
\begin{pmatrix}
x \
y
\end{pmatrix}=
\begin{pmatrix}
1 \
0
\end{pmatrix}x+
\begin{pmatrix}
0 \
1
\end{pmatrix}y \
=x.\vec{e_1}+y.\vec{e_2}
$$
观察下这个列的表达方式其实就是二维平面的标准单位向量, 就是(x,y)这个点坐标的定义,在(1,0)轴上的分量为x,(0,1)轴上的分量为y.

相当于矩阵乘法过程中，我们按列看待这个单位矩阵，第一列就代表一个轴的方向$\vec{e_1}$，第二列代表第二个轴的方向$\vec{e_2}$ ,然后第一个轴和第一个元素相乘加上第二个轴和第二个元素相乘. 换句话说，整个二维空间就只需要这两个轴定义，这个矩阵就定义了两个坐标轴,矩阵表示了整个二维空间.

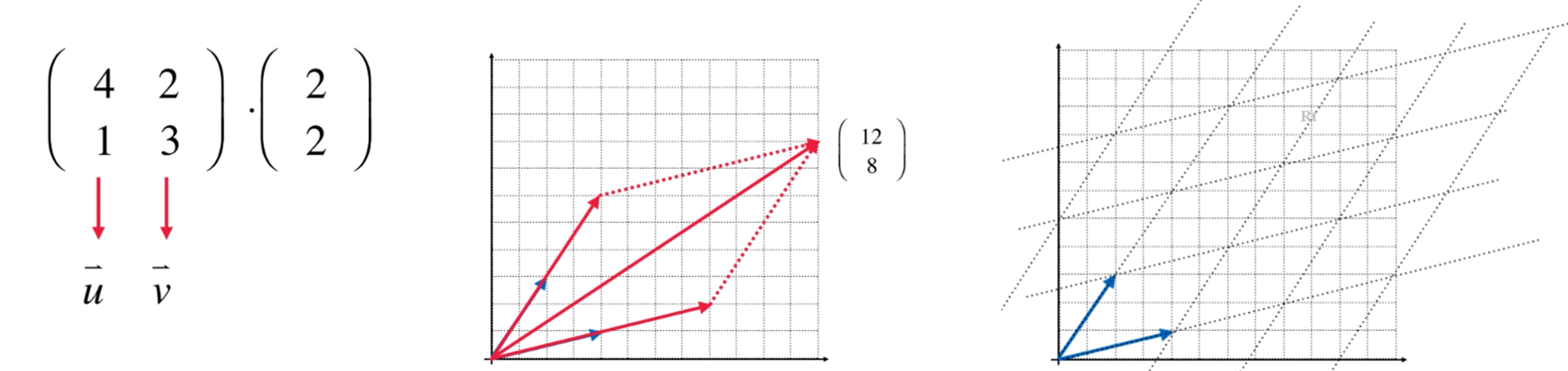
以任意一个矩阵为例：

将第一列$(4,1)^T$ 记做$\vec{u}$ ,第二列$(2,3)^T$ 记做$\vec{v}$ ,这个矩阵就代表了一个由u和v两个向量组成的空间. 此时(2,2)这个点就相当于分别沿u和v走两步，相加最终结果为（12，8）. 最右侧虚线就是这两个坐标轴组成的新的空间.

总结看待矩阵的四个视角

矩阵到底能够能表示什么？

第一个视角就是数据，数据科学中我们常见的，m行n列的数据，每一行代表样本，每一列代表特征
第二个视角是线性代数领域关注的视角-系统，矩阵表示线性方程组线性系统
第三个视角是看做向量的函数(变换)，上面的图形变换就是很典型的例子
第四个视角是空间，矩阵和向量相乘就可以理解成这个向量在矩阵所表示的空间所对应的位置是哪.

Linear Algebra(3):矩阵2